红黑树原理详解及golang实现

红黑树原理详解及golang实现

在看红黑树原理之前，先看下二叉查找树。

二叉查找树

二叉查找树，又称二叉排序树，二叉搜索树。

性质

它具备以下性质：

1、左子树上的所有节点均小于它的根节点值。
2、右子树上的所有节点的值均大于它根节点的值。
3、左右子树也分别为二叉排序树。
4、没有键值相等的节点。

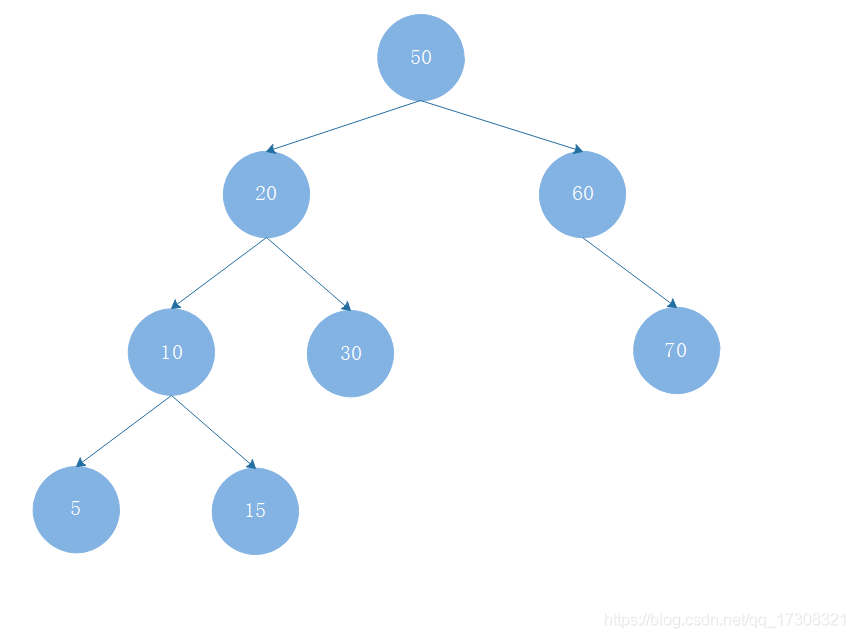
Alt text

既然叫搜索树，那这种结构的好处当然也就是搜索咯，
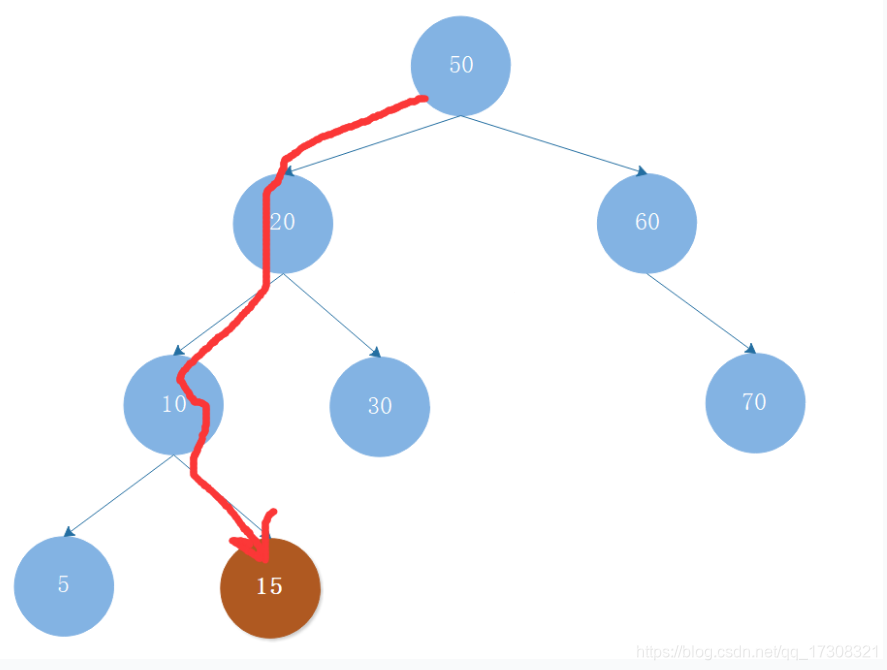
假如我们要查找15

1、从root节点开始，15<50，找左子树。
2、15<20，找左子树，
3、15>10，找右子树，这样便找到15了。

插入也是类似方法，一层一层比较大小，找到合适的位置插入。
在这里插入图片描述

时间复杂度
看见它查找的次数等同于树的高度，在最好的情况下，其平均查找次数和log 2 (n)成正比。
当然也有坏情况，当先后插入的关键字有序时，构成的二叉排序树蜕变为单支树，树的深度和其节点数成正比(和顺序查找相同）.
例如依序插入： 100、200、90、80、70、60、50、40
就会成为如下图形态：
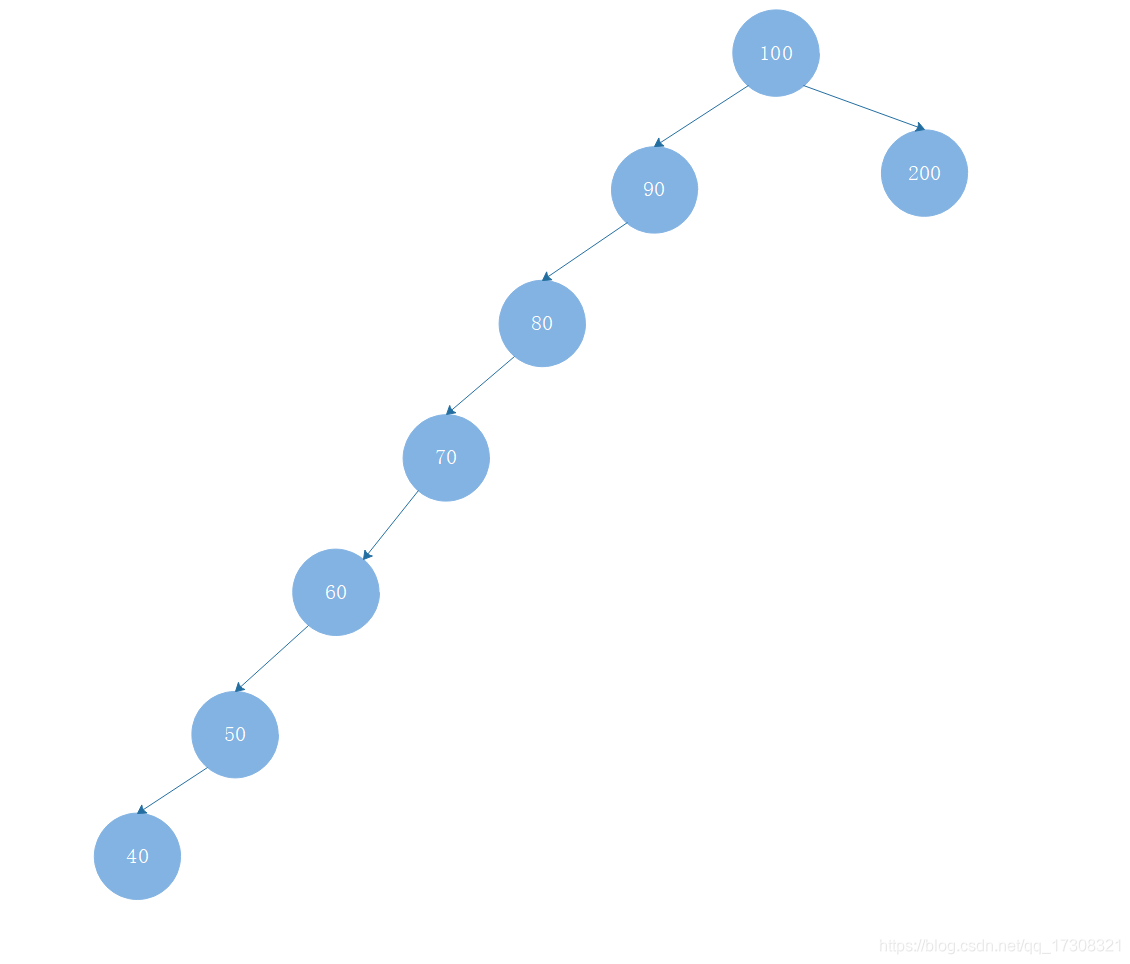
Alt text

为了解决这种不平衡的情形，就有了红黑树。

红黑树

性质

红黑树是一种自平衡的二叉搜索树，它包含了二叉搜索树的特性，同时具备以下性质：

1、所有节点的颜色不是红色就是黑色。
2、根节点是黑色。
3、每个叶子节点都是黑色的空节点(nil)。
4、每个红色节点的两个子节点都是黑色。(从每个叶子到根节点的所有路径上不能有两个连续的红色节点)
5、从任一节点到其叶子节点的所有路径上都包含相同数目的黑节点。

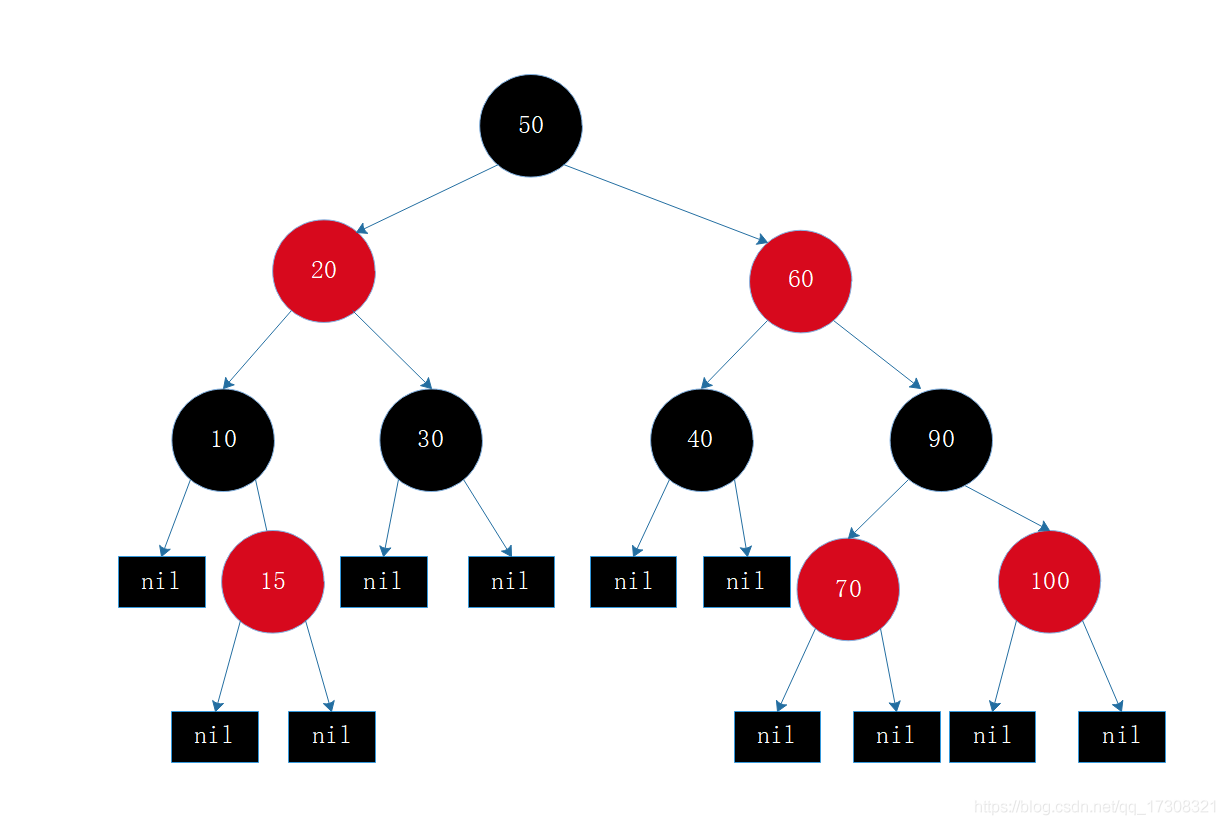
Alt text

前四都能理解其意思吧，所以只解释下第五点，比如60这个节点，到其所有叶子节点的路径都只包含1个黑色节点：40和90。

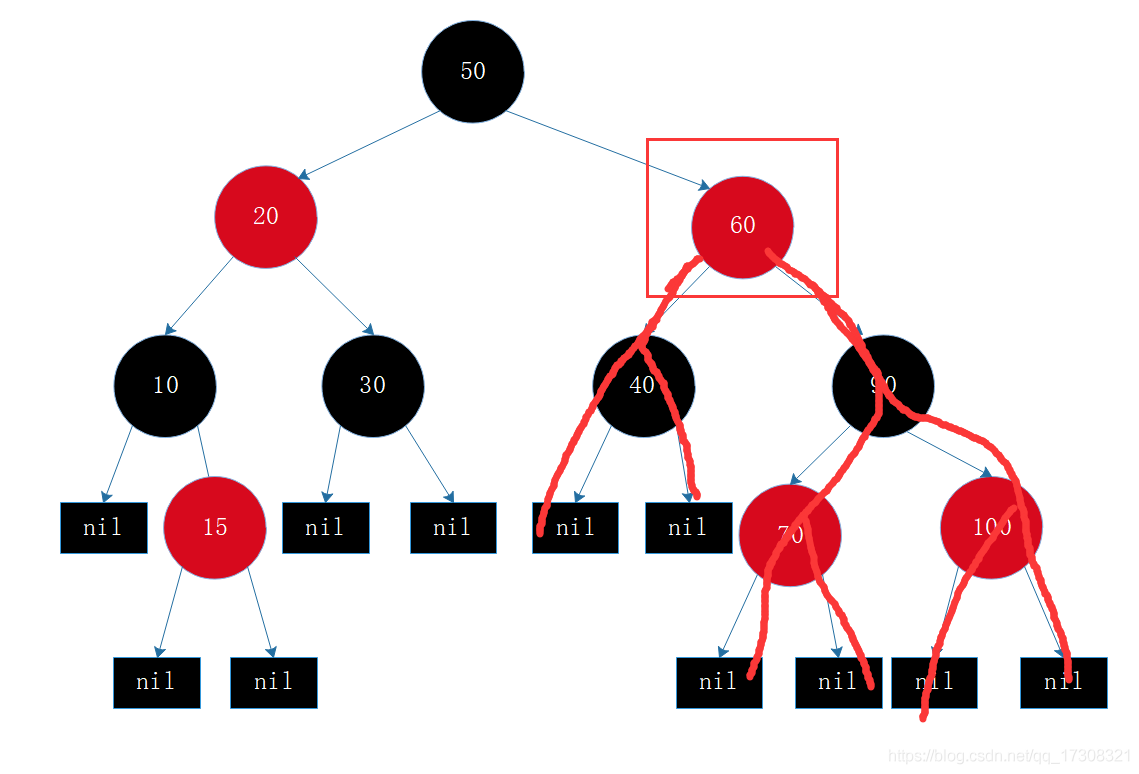
Alt text

operation

红黑树为了维持它的这5点性质，于是它支持了这么几个操作，

变色 ：顾名思义变色，红变黑，黑变红。
左旋转 : 这里借用百度百科两张旋转图，以图中红色节点为中心，中心节点为右孩子替代，而自己成为它的左孩子，同时节点b作为pivot的有孩子(至于为什么是右孩子，b原本就在pivot的右子树上，所以肯定大于pivot)。
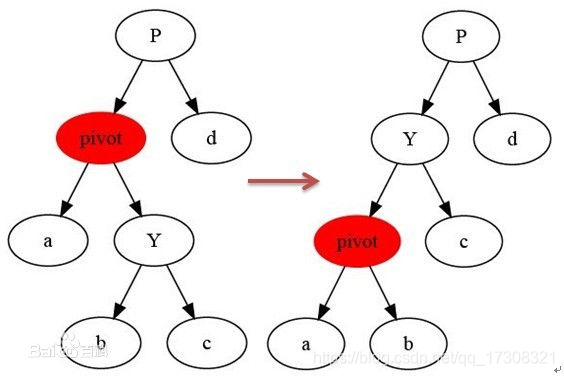
Alt text

右选装 : 同左旋转，中心点顺时钟旋转，成为其原来左孩子的右孩子，原来左孩子的右孩子则成为原中心点的左孩子。
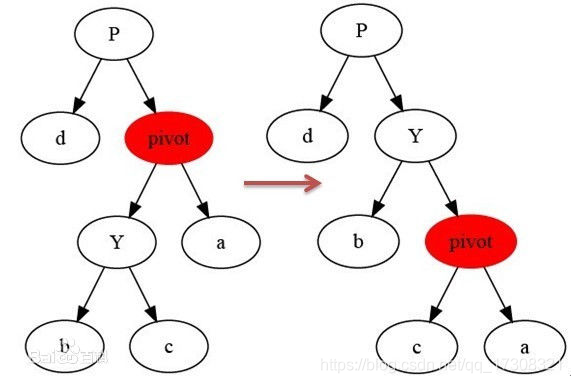
Alt text

接着看看红黑树的插入，看看它是如何通过这几个op维持红黑树这5个性质的。

红黑树的插入

关于插入的特点： 由于性质5的约束，每次插入的节点颜色必然为红色。

插入的化存在几种情形，复杂的树可能会涉及到循环的向树上检索做自平衡，这里先从一颗空树开始先简单理解下这些情形。

`情形1`：空树

直接插入，直接作为根节点，同时由于性质1的约束，通过变色op变为黑色即可。

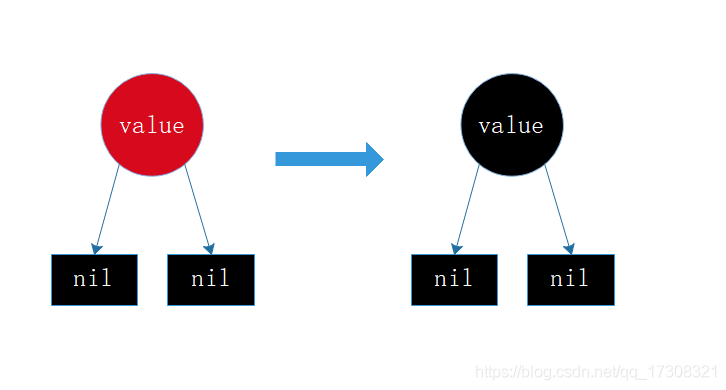
Alt text

`情形2`：插入节点父节为黑色，

不违反任何性质，无需做任何修改。

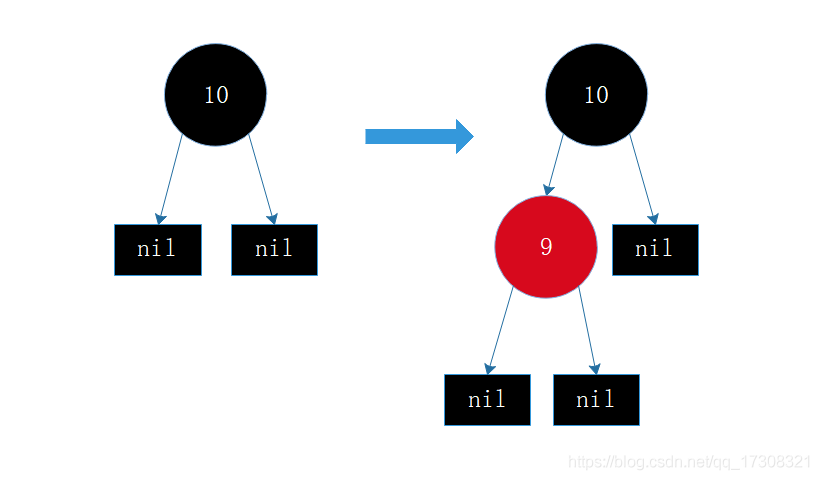
Alt text

`情形3` 插入节点的父节点为红色，父节点为父父节点的左孩子，父父节点的右孩子为黑色，插入节点为左孩子(或者父节点为父父节点的右孩子，父父节点的左孩子为黑色，插入节点为右孩子)。

这是一种插入节点和父节点在一个方向上的情况(例如父节点为左孩子，插入节点也为左孩子)和情形5相反

父节点及父父节点变色，再进行左/右旋转，具体左还是右看你插入的节点的父节点是左子树还是右子树，图例为左子树。

此处 : 变色 - > 右旋转

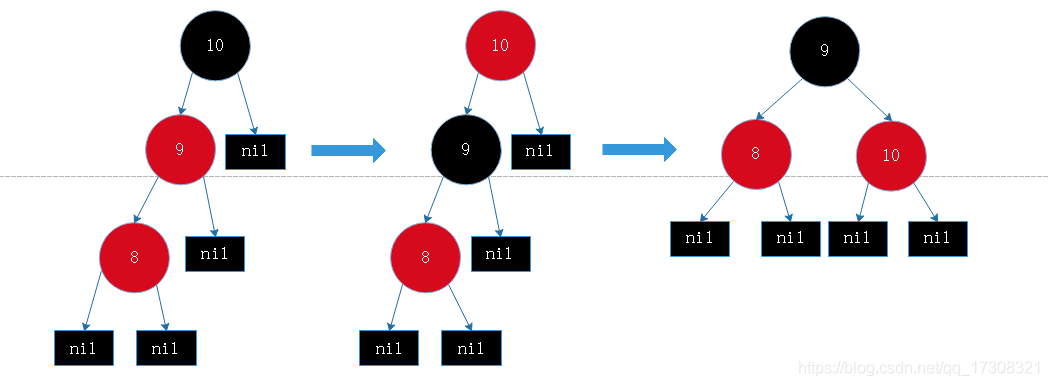
Alt text

`情形4` 插入节点父节点为红色，父父节点的左/右孩子为红色

先将父节点和父父节点右孩子变黑，父父节点变红，然后将父节点当做新插入的红色节点一样递归向上进行平衡红黑树性质操作。若父节点为根节点直接变父节点为黑色即可.

此处 : 变色 -> 变色

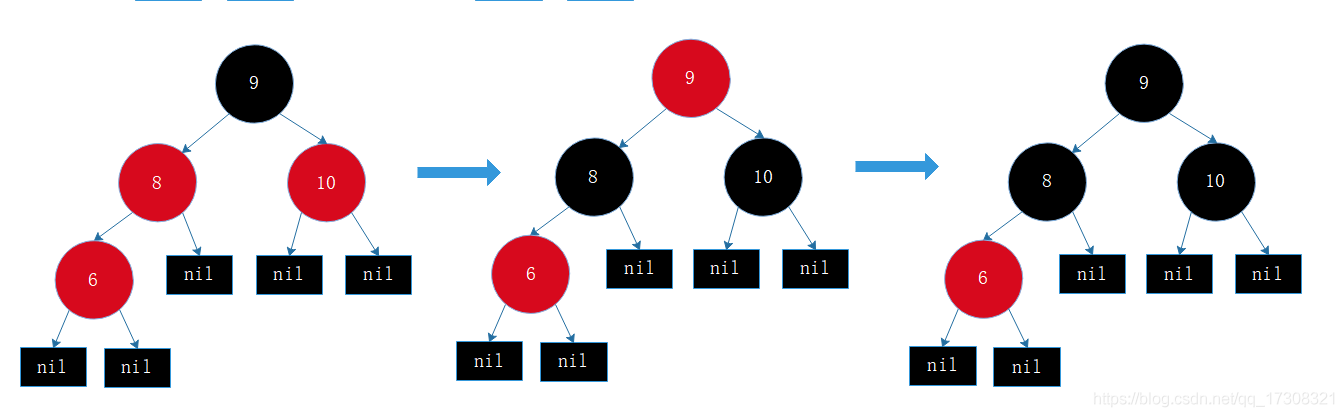
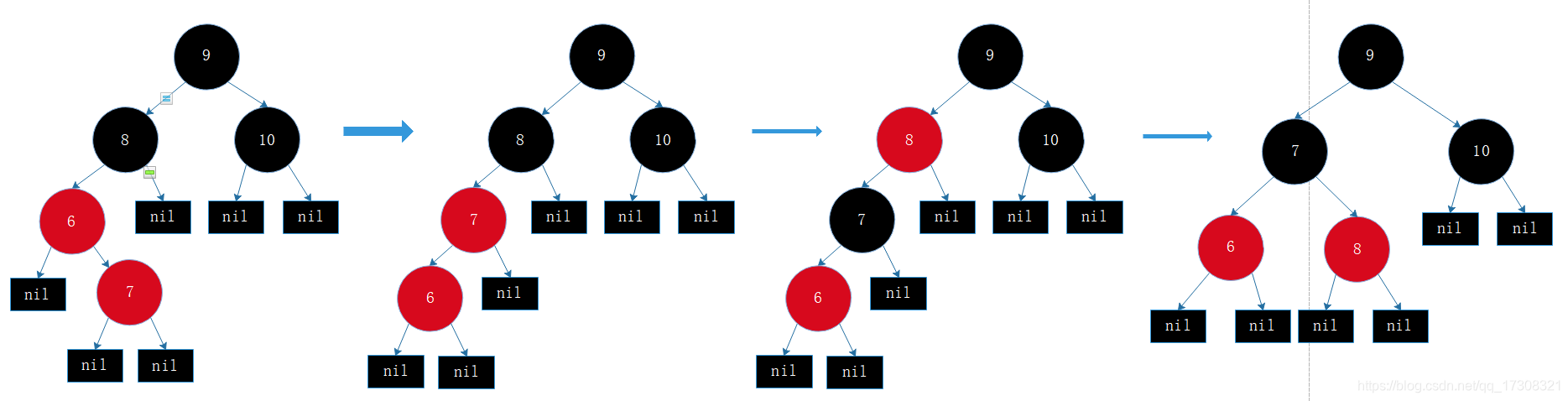
Alt text

`情形5` 插入节点的父节点为红色，父节点为父父节点的左孩子，父父节点的右孩子为黑色，插入节点为右孩子(或者父节点为父父节点的右孩子，父父节点的左孩子为黑色，插入节点为左孩子)。

和情形3类比是一种反向情况，这种情况进行两次旋转，
先左/右旋转，旋转后变成了情形3，接着按情形3变换即可。

此处：左旋转 -> 变色 -> 右旋转
Alt text

golang实现

类型定义

需要注意的是红黑树的NIL节点需要单独定义出来，不能直接用nil哦。

const (
	RED = true
	BLACK = false
)

type Node struct {
	Parent *Node
	Left   *Node
	Right  *Node
	color  bool
	Item
}

type Rbtree struct {
	NIL  *Node
	root *Node
	count uint64
}

func New() *Rbtree{
	node := Node{nil, nil, nil, BLACK, nil}
	return &Rbtree{
		NIL   : &node,
		root  : &node,
		count : 0,
	}
}

leftRotate

// Left Rotate
func (rbt *Rbtree) LeftRotate(no *Node) {
	// Since we are doing the left rotation, the right child should *NOT* nil.
	if no.Right == nil {
		return
	}

	//          |                                  |
	//          X                                  Y
	//         / \         left rotate            / \
	//        α  Y       ------------->         X   γ
	//           / \                            / \
	//          β  γ                            α  β

	rchild := no.Right
	no.Right = rchild.Left

	if rchild.Left != nil {
		rchild.Left.Parent = no
	}

	rchild.Parent = no.Parent

	if no.Parent == nil {
		rbt.root = rchild
	} else if no == no.Parent.Left {
		no.Parent.Left = rchild
	} else {
		no.Parent.Right = rchild
	}

	rchild.Left = no

	no.Parent = rchild

}

func LeftRotateTest(){
	var i10 Int = 10
	var i12 Int = 12

	rbtree := New()
	x := &Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, BLACK, i10}
	rbtree.root = x
	y := &Node{rbtree.root.Right, rbtree.NIL, rbtree.NIL, RED, i12}
	rbtree.root.Right = y

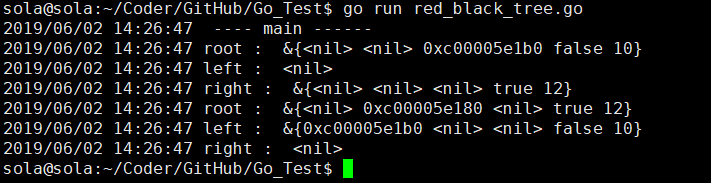
	log.Println("root : ", rbtree.root)
	log.Println("left : ", rbtree.root.Left)
	log.Println("right : ", rbtree.root.Right)

	rbtree.LeftRotate(rbtree.root)
	
	log.Println("root : ", rbtree.root)
	log.Println("left : ", rbtree.root.Left)
	log.Println("right : ", rbtree.root.Right)

}

Alt text

RightRotate

// Right Rotate
func (rbt *Rbtree) RightRotate(no *Node) {
	if no.Left == nil {
		return
	}

	//          |                                  |
	//          X                                  Y
	//         / \         right rotate           / \
	//        Y   γ      ------------->         α  X
	//       / \                                    / \
	//      α  β                                    β  γ

	lchild := no.Left
	no.Left = lchild.Right

	if lchild.Right != nil {
		lchild.Right.Parent = no
	}

	lchild.Parent = no.Parent

	if no.Parent == nil {
		rbt.root = lchild
	} else if no == no.Parent.Left {
		no.Parent.Left = lchild
	} else {
		no.Parent.Right = lchild
	}

	lchild.Right = no

	no.Parent = lchild

}

func RightRotateTest(){
	var i10 Int = 10
	var i12 Int = 12

	rbtree := New()
	x := &Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, BLACK, i10}
	rbtree.root = x
	y := &Node{rbtree.root.Right, rbtree.NIL, rbtree.NIL, RED, i12}
	rbtree.root.Right = y

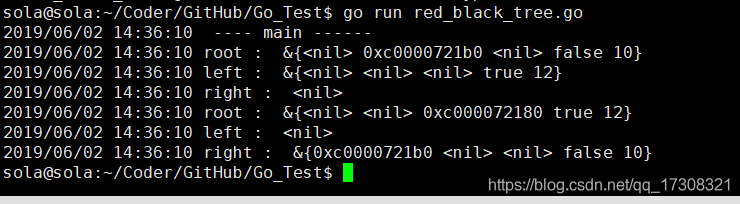
	log.Println("root : ", rbtree.root)
	log.Println("left : ", rbtree.root.Left)
	log.Println("right : ", rbtree.root.Right)

	rbtree.RightRotate(rbtree.root)
	
	log.Println("root : ", rbtree.root)
	log.Println("left : ", rbtree.root.Left)
	log.Println("right : ", rbtree.root.Right)

}

Alt text

Item Interface

值类型接口

type Item interface {
	Less(than Item) bool
}

type Int int

func (x Int) Less(than Item) bool {
	log.Println(x, " ", than.(Int))
	return x < than.(Int)
}

type Uint32 uint32

func (x Uint32) Less(than Item) bool {
	log.Println(x, " ", than.(Uint32))
	return x < than.(Uint32)
}

type String string

func (x String) Less(than Item) bool {
	log.Println(x, " ", than.(String))
	return x < than.(String)
}

func ItemTest(){
	var itype1 Int = 10
	var itype2 Int = 12

	log.Println(itype1.Less(itype2))


	var strtype1 String = "sola"
	var strtype2 String = "ailumiyana"

	log.Println(strtype1.Less(strtype2))
}

Alt text

insert

func (rbt *Rbtree) Insert(no *Node) {
	x := rbt.root
	var y *Node = rbt.NIL

	for x != rbt.NIL {
		y = x 
		if less(no.Item, x.Item) {
			x = x.Left
		} else if less(x.Item, no.Item) {
			x = x.Right
		} else {
			log.Println("that node already exist")
		}
	}

	no.Parent = y
	if y == rbt.NIL {
		rbt.root = no
	} else if less(no.Item, y.Item) {
		y.Left = no
	} else {
		y.Right = no
	}

	rbt.count++
	rbt.insertFixup(no)

}

func (rbt *Rbtree) insertFixup(no *Node) {
	for no.Parent.color == RED {
		if no.Parent == no.Parent.Parent.Left {
			y := no.Parent.Parent.Right
			if y.color == RED {
				//
				// 情形 4

				log.Println("TRACE Do Case 4 :", no.Item)

				no.Parent.color = BLACK
				y.color = BLACK
				no.Parent.Parent.color = RED
				no = no.Parent.Parent  //循环向上自平衡.
			} else {
				if no == no.Parent.Right {
					//
					// 情形 5 : 反向情形
					// 直接左旋转 , 然后进行情形3(变色->右旋)
					log.Println("TRACE Do Case 5 :", no.Item)

					if no == no.Parent.Right {
						no = no.Parent
						rbt.LeftRotate(no)
					}
				}
				log.Println("TRACE Do Case 6 :", no.Item)

				no.Parent.color = BLACK
				no.Parent.Parent.color = RED
				rbt.RightRotate(no.Parent.Parent)
			}
		} else { //为父父节点右孩子情形，和左孩子一样，改下转向而已.
			y := no.Parent.Parent.Left
			if y.color == RED {
				no.Parent.color = BLACK
				y.color = BLACK
				no.Parent.Parent.color = RED
				no = no.Parent.Parent
			} else {
				if no == no.Parent.Left {
					no = no.Parent
					rbt.RightRotate(no)
				}
				
				no.Parent.color = BLACK
				no.Parent.Parent.color = RED
				rbt.LeftRotate(no.Parent.Parent)
			}
		}
	}
	rbt.root.color = BLACK
}

func InsertTest(){
	rbtree := New()

	rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(10)})
	rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(9)})
	rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(8)})
	rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(6)})
	rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(7)})

	log.Println("rbtree counts : ", rbtree.count)

	log.Println("------ ", rbtree.root.Item)
	log.Println("----", rbtree.root.Left.Item, "---", rbtree.root.Right.Item)
	log.Println("--", rbtree.root.Left.Left.Item, "-", rbtree.root.Left.Right.Item)

}

InsertTest() 仔细瞧瞧这就是我们讲情形那棵树哈。

Alt text

完整代码

package main

import(
	"log"
)

const (
	RED = true
	BLACK = false
)

//-----------------------------------
//Item interface
//
type Item interface {
	Less(than Item) bool
}

type Int int

func (x Int) Less(than Item) bool {
	log.Println(x, " ", than.(Int))
	return x < than.(Int)
}

type Uint32 uint32

func (x Uint32) Less(than Item) bool {
	log.Println(x, " ", than.(Uint32))
	return x < than.(Uint32)
}

type String string

func (x String) Less(than Item) bool {
	log.Println(x, " ", than.(String))
	return x < than.(String)
}

//-----------------------------------

type Node struct {
	Parent *Node
	Left   *Node
	Right  *Node
	color  bool
	Item
}

type Rbtree struct {
	NIL  *Node
	root *Node
	count uint64
}

func New() *Rbtree{
	node := &Node{nil, nil, nil, BLACK, nil}
	return &Rbtree{
		NIL   : node,
		root  : node,
		count : 0,
	}
}

func less(x, y Item) bool {
	return x.Less(y)
}

// Left Rotate
func (rbt *Rbtree) LeftRotate(no *Node) {
	// Since we are doing the left rotation, the right child should *NOT* nil.
	if no.Right == rbt.NIL {
		return
	}

	//          |                                  |
	//          X                                  Y
	//         / \         left rotate            / \
	//        α  Y       ------------->         X   γ
	//           / \                            / \
	//          β  γ                            α  β

	rchild := no.Right
	no.Right = rchild.Left

	if rchild.Left != rbt.NIL {
		rchild.Left.Parent = no
	}

	rchild.Parent = no.Parent

	if no.Parent == rbt.NIL {
		rbt.root = rchild
	} else if no == no.Parent.Left {
		no.Parent.Left = rchild
	} else {
		no.Parent.Right = rchild
	}

	rchild.Left = no

	no.Parent = rchild

}

// Right Rotate
func (rbt *Rbtree) RightRotate(no *Node) {
	if no.Left == rbt.NIL {
		return
	}

	//          |                                  |
	//          X                                  Y
	//         / \         right rotate           / \
	//        Y   γ      ------------->         α  X
	//       / \                                    / \
	//      α  β                                    β  γ

	lchild := no.Left
	no.Left = lchild.Right

	if lchild.Right != rbt.NIL {
		lchild.Right.Parent = no
	}

	lchild.Parent = no.Parent

	if no.Parent == rbt.NIL {
		rbt.root = lchild
	} else if no == no.Parent.Left {
		no.Parent.Left = lchild
	} else {
		no.Parent.Right = lchild
	}

	lchild.Right = no

	no.Parent = lchild

}

func (rbt *Rbtree) Insert(no *Node) {
	x := rbt.root
	var y *Node = rbt.NIL

	for x != rbt.NIL {
		y = x 
		if less(no.Item, x.Item) {
			x = x.Left
		} else if less(x.Item, no.Item) {
			x = x.Right
		} else {
			log.Println("that node already exist")
		}
	}

	no.Parent = y
	if y == rbt.NIL {
		rbt.root = no
	} else if less(no.Item, y.Item) {
		y.Left = no
	} else {
		y.Right = no
	}

	rbt.count++
	rbt.insertFixup(no)

}

func (rbt *Rbtree) insertFixup(no *Node) {
	for no.Parent.color == RED {
		if no.Parent == no.Parent.Parent.Left {
			y := no.Parent.Parent.Right
			if y.color == RED {
				//
				// 情形 4

				log.Println("TRACE Do Case 4 :", no.Item)

				no.Parent.color = BLACK
				y.color = BLACK
				no.Parent.Parent.color = RED
				no = no.Parent.Parent  //循环向上自平衡.
			} else {
				if no == no.Parent.Right {
					//
					// 情形 5 : 反向情形
					// 直接左旋转 , 然后进行情形3(变色->右旋)
					log.Println("TRACE Do Case 5 :", no.Item)

					if no == no.Parent.Right {
						no = no.Parent
						rbt.LeftRotate(no)
					}
				}
				log.Println("TRACE Do Case 6 :", no.Item)

				no.Parent.color = BLACK
				no.Parent.Parent.color = RED
				rbt.RightRotate(no.Parent.Parent)
			}
		} else { //为父父节点右孩子情形，和左孩子一样，改下转向而已.
			y := no.Parent.Parent.Left
			if y.color == RED {
				no.Parent.color = BLACK
				y.color = BLACK
				no.Parent.Parent.color = RED
				no = no.Parent.Parent
			} else {
				if no == no.Parent.Left {
					no = no.Parent
					rbt.RightRotate(no)
				}
				
				no.Parent.color = BLACK
				no.Parent.Parent.color = RED
				rbt.LeftRotate(no.Parent.Parent)
			}
		}
	}
	rbt.root.color = BLACK
}

func LeftRotateTest(){
	var i10 Int = 10
	var i12 Int = 12

	rbtree := New()

	x := &Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, BLACK, i10}
	rbtree.root = x
	y := &Node{rbtree.root.Right, rbtree.NIL, rbtree.NIL, RED, i12}
	rbtree.root.Right = y

	log.Println("root : ", rbtree.root)
	log.Println("left : ", rbtree.root.Left)
	log.Println("right : ", rbtree.root.Right)

	rbtree.LeftRotate(rbtree.root)
	
	log.Println("root : ", rbtree.root)
	log.Println("left : ", rbtree.root.Left)
	log.Println("right : ", rbtree.root.Right)

}

func RightRotateTest(){
	var i10 Int = 10
	var i12 Int = 12
	
	rbtree := New()

	x := &Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, BLACK, i10}
	rbtree.root = x
	y := &Node{rbtree.root.Right, rbtree.NIL, rbtree.NIL, RED, i12}
	rbtree.root.Left = y

	log.Println("root : ", rbtree.root)
	log.Println("left : ", rbtree.root.Left)
	log.Println("right : ", rbtree.root.Right)

	rbtree.RightRotate(rbtree.root)
	
	log.Println("root : ", rbtree.root)
	log.Println("left : ", rbtree.root.Left)
	log.Println("right : ", rbtree.root.Right)

}

func ItemTest(){
	var itype1 Int = 10
	var itype2 Int = 12

	log.Println(itype1.Less(itype2))


	var strtype1 String = "sola"
	var strtype2 String = "ailumiyana"

	log.Println(strtype1.Less(strtype2))
}

func InsertTest(){
	rbtree := New()

	rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(10)})
	rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(9)})
	rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(8)})
	rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(6)})
	rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(7)})

	log.Println("rbtree counts : ", rbtree.count)

	log.Println("------ ", rbtree.root.Item)
	log.Println("----", rbtree.root.Left.Item, "---", rbtree.root.Right.Item)
	log.Println("--", rbtree.root.Left.Left.Item, "-", rbtree.root.Left.Right.Item)

}


func main()  {
	log.Println(" ---- main ------ ")
	LeftRotateTest()
	RightRotateTest()
	ItemTest()
	InsertTest()
}

小结

好了本文对红黑树的讲解到此结束，刚开始看红黑树的时候这些性质确实特别绕，但是理解了这5点性质，就好多了。然后就是两个操作： 变色和旋转 理解红黑树是通过他们进行自平衡的就行了。
由于时间原因只写了插入了，没做删除，有机会再补上吧，不过理解了插入原理，删除也不在话下了吧。

posted @ 2019-06-02 17:53 靑い空゛阅读(4150) 评论(3) 编辑收藏举报

刷新页面返回顶部

靑い空゛

一歩ずつ歩み続けてはじめて千里の遠くに行き着けるし

红黑树原理详解及golang实现

红黑树原理详解及golang实现

二叉查找树

性质

红黑树

性质

operation

红黑树的插入

`情形1`：空树

`情形2`：插入节点父节为黑色，

`情形3` 插入节点的父节点为红色，父节点为父父节点的左孩子，父父节点的右孩子为黑色，插入节点为左孩子(或者父节点为父父节点的右孩子，父父节点的左孩子为黑色，插入节点为右孩子)。

`情形4` 插入节点父节点为红色，父父节点的左/右孩子为红色

`情形5` 插入节点的父节点为红色，父节点为父父节点的左孩子，父父节点的右孩子为黑色，插入节点为右孩子(或者父节点为父父节点的右孩子，父父节点的左孩子为黑色，插入节点为左孩子)。

golang实现

类型定义

leftRotate

RightRotate

Item Interface

insert

完整代码

小结

公告

靑い空゛

一歩ずつ歩み続けてはじめて千里の遠くに行き着けるし

红黑树原理详解及golang实现

红黑树原理详解及golang实现

二叉查找树

性质

红黑树

性质

operation

红黑树的插入

情形1：空树

情形2：插入节点父节为黑色，

情形3 插入节点的父节点为红色，父节点为父父节点的左孩子，父父节点的右孩子为黑色，插入节点为左孩子(或者父节点为父父节点的右孩子，父父节点的左孩子为黑色，插入节点为右孩子)。

情形4 插入节点父节点为红色，父父节点的左/右孩子为红色

情形5 插入节点的父节点为红色，父节点为父父节点的左孩子，父父节点的右孩子为黑色，插入节点为右孩子(或者父节点为父父节点的右孩子，父父节点的左孩子为黑色，插入节点为左孩子)。

golang实现

类型定义

leftRotate

RightRotate

Item Interface

insert

完整代码

小结

公告

`情形1`：空树

`情形2`：插入节点父节为黑色，

`情形3` 插入节点的父节点为红色，父节点为父父节点的左孩子，父父节点的右孩子为黑色，插入节点为左孩子(或者父节点为父父节点的右孩子，父父节点的左孩子为黑色，插入节点为右孩子)。

`情形4` 插入节点父节点为红色，父父节点的左/右孩子为红色

`情形5` 插入节点的父节点为红色，父节点为父父节点的左孩子，父父节点的右孩子为黑色，插入节点为右孩子(或者父节点为父父节点的右孩子，父父节点的左孩子为黑色，插入节点为左孩子)。