直接法(Direct Method)计算相机位置和姿态

1. 直接法的思想

我们在<LK光流法跟踪特征点>这篇文章介绍了如何跟踪某个像素并形成轨迹。事实上跟踪这些特征点的最终目的还是为了计算相机的位置和姿态变化。今天我们要介绍的直接法就是不先计算像素的轨迹而是直接计算出相机的位置和姿态。直接法的思想是：“同一个块它的灰度值是不会发生变化的（这和光流法非常像）。比如说我们相机绕着一个球去拍摄。那么时刻t的这帧里面球所在的那块像素的灰度值，与它在时刻t+dt这帧图片中球所在的那块像素灰度值相同。唯一变化的是球所在的那个像素块在图片中的相对位置发生了变化。变化了的原因是因为相机的位置和姿态发生了变化。我们要做的是求出相机怎么位置和姿态怎么发生了怎样的变化。那么怎么求呢？我们先假设相机发生了某种变化$R$，假设球在时刻t的那帧图片中的位置是$p_1$（看看后面那张图）。那么在t+dt时刻那帧图片中球的位置就是$p_2=Rp_1$。现在已知$p_1$和$p_2$处的像素灰度值一样，要求得$R$。我们可以遍历$R$的各种取值，如何评价这个取值好不好呢？我只需要比对用选定的那个R计算出的$p_2$那个地方的灰度值与$p_1$处的灰度值是否接近。直接法的思想就是这么简单。”。我们知道LK光流法它是需要先提取特征点，但是直接法是不需要提取特征点的所以计算复杂度更低适合嵌入式这种计算资源有限的场合。

2. 直接法的推导

2.1误差模型

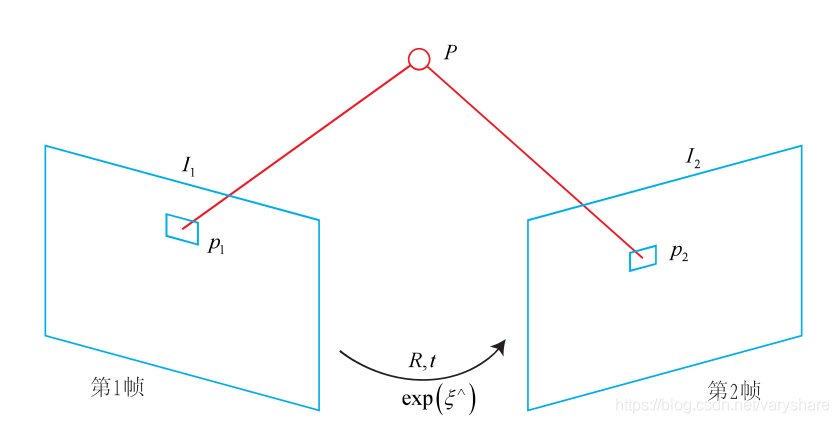
我们假设相机发生了某种旋转和平移变换，旋转矩阵是R平移量是t。我们可以用一个变换矩阵T来表示旋转R+平移t。我们要做到的就是求出T。根据什么求出T？根据第1帧上$p_1$所在的那块像素的灰度值，应该与第2帧$p_2$所在的那个块的像素的灰度值一样来计算矩阵T。那$p_1$与$p_2$又是什么关系？答：是同一个物体在不同视角下拍摄到的像素块。举个例子解释下：假设$p_1$那个像素块是个球，我希望相机进行了变换T之后（$p_1$那个点就变成了$p_2=Tp_1$），我希望$p_2$这个像素块也是个球。当然我们只会比对$p_1$和$p_2$这两块像素灰度值是否一样。很明显这是个优化问题，因为$T$设置一个值，那么就会计算出一个$p_2$。计算出一个$p_2$那么我就得看看它是否是与$p_1$那个块足够相似。我们假设$p_1$与$p_2$之间的灰度值误差是：$error(T)=I_1(p_1)-I_2(p_2)=I_1(p_1)-I_2(Tp_1)$。我们就是要从T的不同取值中找一个不错的解来最小化这个误差。此时的这个T就是相机发生的位置和姿态变换矩阵。

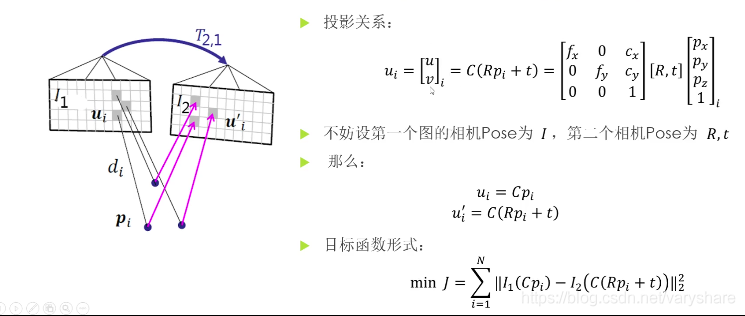
接下来要做的事就是根据误差模型求解最优的T，我们可以用高斯牛顿法或者列文伯格方法求解到让error(T)最小的T。

2.2求解让误差最小的变换矩阵T

而这两种方法不管是哪一种都是要求$e(T)$对变换矩阵$T$的导数。对这个随时间变化的矩阵求导这个可不是平常我们简简单单的求导。这要用到李群求导的知识。变换矩阵$T$就是一个李群（可以视作一个指数函数$e^{(\xi^\wedge)}$），它的自变量是${\xi^\wedge}$（李群的自变量叫做李代数）。也就是说$T=e^{(\xi^\wedge)}$.于是误差函数变为：
$error(T)=error(e^{(\xi^\wedge)})=I(p_1)-I(e^{(\xi^\wedge)}p_1)$。对李群求导一般是用定义法求导数（被叫做李代数上的扰动模型，因为定义法求导就是李代数加上一个微小的增量，这个增量被视作是一个微小扰动）。即用$e^{(\xi^\wedge+\Delta \xi ^\wedge)}$来替换原先的$e^{(\xi^\wedge)}$。
（下面这部分是参考高翔博士写的，但是他这部分写得过渡性不够好，比较难理解。然后我补充了泰勒展开的细节
于是误差模型就变成了：
$error(e^{(\xi^\wedge+\Delta \xi ^\wedge)})\\ =I(p_1)-I(e^{(\xi^\wedge+\Delta \xi ^\wedge)}p_1) \\ =I(p_1)-I(e^{\xi^\wedge}e^{\Delta \xi ^\wedge}p_1) \\ \\ 对e^{\Delta \xi ^\wedge}在0处进行泰勒展开得\\ \approx I(p_1)-I(e^{(\xi^\wedge)}(1+\Delta \xi ^\wedge)p_1) \\ =I(p_1)-I(e^{(\xi^\wedge)} p_1+e^{(\xi^\wedge)}e^{\Delta \xi ^ \wedge} p_1)$
注意：然后我们对$I(e^{(\xi^\wedge)} p_1+e^{(\xi^\wedge)}e^{\Delta \xi ^ \wedge} p_1)$在$e^{(\xi^\wedge)} p_1$处（进行一阶泰勒展开即把$e^{(\xi^\wedge)} p_1$视作常数，$\Delta \xi$视作自变量）得到：
$=I(p_1)-I(e^{(\xi^\wedge)} p_1)-\frac {dI}{d e^{(\xi^\wedge)}e^{\Delta \xi ^ \wedge} p_1} \frac {d e^{(\xi^\wedge)}e^{\Delta \xi ^ \wedge} p_1}{d\Delta \xi } {\Delta \xi }$
也就是说误差模型变成了：
$error(e^{(\xi^\wedge+\Delta \xi ^\wedge)})=error(e^{(\xi^\wedge)})-\frac {dI}{d e^{(\xi^\wedge)}e^{\Delta \xi ^ \wedge} p_1} \frac {d e^{(\xi^\wedge)}e^{\Delta \xi ^ \wedge} p_1}{d\Delta \xi } {\Delta \xi }$
然后根据定义法求导：
$lim \frac {error(e^{(\xi^\wedge+\Delta \xi ^\wedge)})-error(e^{(\xi^\wedge)}}{\Delta \xi ^\wedge}$

参考文献：
[1] https://blog.csdn.net/Kevin_cc98/article/details/70920700
[2] https://www.cnblogs.com/gaoxiang12/p/5689927.html#mjx-eqn-eqjacobianofDirect
[3] https://arxiv.org/pdf/1607.02565.pdf