我是如何十分钟复习概率论基础知识？

概率论中那些符号

联合概率

p(x,y) = x和y同时发生的概率。当x与y是两个没有任何联系的事情的时候那么p(x,y)=p(x)p(y)。比如：你今天是否吃饭这个事和太阳是否从东边出来这就是两个没有任何联系的事。你今天吃不吃饭跟太阳出不出来并没有任何关系。两件事没有任何联系在学术上叫做这两件事相互独立，你这件事发生不干扰我，我这件事发生也不干扰你。

条件概率

那有哪些事件是不相互独立的呢？你今天是否吃饭这个事，与你今天参加马拉松拿第一名是不相互独立的。如果在你今天会吃饭的条件下马拉松拿第一的概率会更高。像这种有前提条件的事件发生的概率叫做条件概率。用公式表示就是p(x|y)=p(马拉松第一|今天吃饭)。注意：只要见到p(x|y)一定要自动把它翻译成：“在y发生的情况下，x发生的概率”。
条件概率计算公式：$p(x|y)=\frac{p(x,y)}{p(y)}$。
这公式怎么得来的呢？
很简单，遇到你记不住的公式你就画韦恩图。


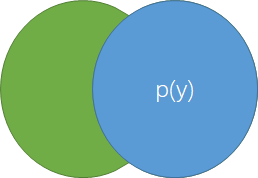
$p(x|y)$表示y已经发生的条件下，也就是说在y那个圆中，x的的占比。这就很容得到$p(x|y)=\frac{p(x,y)}{p(y)}$。

全概率公式

这个公式非常有用，一般很多不好求的概率可以通过全概率公式把各种情况的概率求和即可得到最终的概率。
比如p(x)概率不知道我可以通过$p(x)=\sum_{y_i} p(x|y_i)p(y_i)$这个方式来求概率。

贝叶斯公式

贝叶斯公式就是条件概率。在前面条件概率中我们提到了$p(x,y)=p(x|y)p(y)=p(y|x)p(x)$。而贝叶斯公式就是：$p(x|y)p(y)=p(y|x)p(x)$。由这个公式我们可以得到：

• $p(x|y)=\frac{p(y|x)p(x)}{p(y)}$
• $p(y|x)=\frac{p(x|y)p(y)}{p(x)}$

在全概率公式中我们提到了p(x),p(y)这些概率可以通过另外一种方式求得。
$p(x)=\sum_{y_i} p(x|y_i)p(y_i)$,$p(y)=\sum_{x_i} p(y|x_i)p(x_i)$
所以有：
$p(x|y)=\frac{p(y|x)p(x)}{p(y)}=\frac{p(y|x)p(x)}{\sum_{x_i} p(y|x_i)p(x_i)}$

$p(y|x)=\frac{p(x|y)p(y)}{p(x)}=\frac{p(x|y)p(y)}{\sum_{y_i} p(x|y_i)p(y_i)}$

先验概率、后验概率、似然（likelihood）

在贝叶斯公式$p(x|y)==\frac{p(y|x)p(x)}{p(y)}=\frac{p(y|x)p(x)}{\sum_{x_i} p(y|x_i)p(x_i)}$中：

• $p(x)$就叫做先验概率，为什么？举个例子：你在路上，让你闭眼，问你左边那个人是男是女的概率？你回答说男女的概率都是0.5。没有任何参考信息的情况下的那个概率叫做先验概率。
• $p(x|y)$这个叫做后验概率。我们将这个公式翻译翻译一下就是：在知道y的情况下，x发生的概率。还是上面那个例子：我告诉你现在你在某理工大学，然后你肯定会知道那个人是男的概率应该是80%，是女的概率是20%。知道了信息后再重新计算得到的概率叫做后验概率。事实上我们做的所有推理都是根据后验概率算出的。比如你看到有个人分析它性别：长头发（是女概率增大），有口红（是女概率增大）。用公式表达就是：你想计算p(女|长头发，有口红)这个值。很多机器学习算法就是利用这个思想利用已有的数据来进行推理。
• p(y|x)叫做似然。

举个例子：假如一个机器人走路，不开雷达情况下根据自己的速度和方向估计出现在离某个障碍物距离是x的概率是p(x)。然后它突然开了雷达花了1秒看了下障碍物。在当机器人离目标距离是x的情况下传感器输出距离值是y的概率是p(y|x)。在传感器它以往的数据统计中发现数值y出现的概率是p(y)。在知道传感器测量值是y的情况下，机器人离目标距离是x的概率是p(x|y)。

注意：我们会发现p(y)是$p(x|y)==\frac{p(y|x)p(x)}{p(y)}$中唯一一个跟x没有关系的概率值。这个发现有什么用呢？这意味着p(y)是一个常数，我们只用计算一次即可。
因此有些书会这么写贝叶斯公式：$p(x|y)==\frac{p(y|x)p(x)}{p(y)}=η p(y|x)p(x)$。其中η叫做归一化常数。

贝叶斯多个数据修正推理

当我们判断一个人的性别的时候，我们有可能同时得到两个信息：有口红，长头发。我们平常见到的贝叶斯公式一般是p(x|y)只有一个信息y。
$P(x|y,z)=\frac {P(x,y,z)}{P(y,z)}=\frac{P(y|x,z)P(x,z)}{P(y|z)P(z)}=\frac{P(y|x,z)P(x|z)P(z)}{P(y|z)P(z)}=\frac{P(y|x,z)P(x|z)}{P(y|z)}$

$P(x,y|z)=\frac{P(x,y,z)}{P(z)}=\frac{P(y|x,z)*P(x,z)}{P(z)}=\frac{P(y|x,z)P(x|z)P(z)}{P(z)}=P(y|x,z)P(x|z)$

[1] https://understandinguncertainty.org/
[2] 《bayesian reasoning and machine learning》