机器人理论与实践(1): 差速驱动原理与python编程模拟 （控制模型建模）

本文未经本人@Ai酱许可, [禁止转载]

差速驱动的原理就是：利用左轮和右轮的速度差异来旋转。它的控制命令是[左轮速度，右轮速度，持续时间]。下面这玩意平衡车就是典型的差速驱动。

(图片来自网络)

本文要解决的问题是：在已知控制命令，和机器人当前时刻的位置，朝向；我们如何求得执行完控制命令后机器人的位置和朝向？

博主先介绍了差速运动的轨迹与速度之间的联系，然后介绍如何求执行命令后机器人位置和朝向的理论，最后介绍了Python编程实践。

差速驱动的轨迹与速度之间的联系是什么？

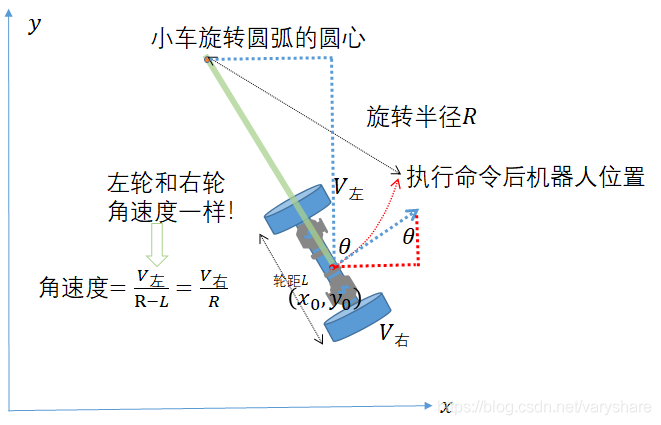
直接看下面这张图，两个轮子速度不同会让机器人绕着某个点旋转，所以轨迹是一段圆弧。所以只要知道旋转半径R那就可以求得机器人执行命令后所在的位置，以及朝向。

%注意：旋转半径R是待求变量，其他变量都是已知。

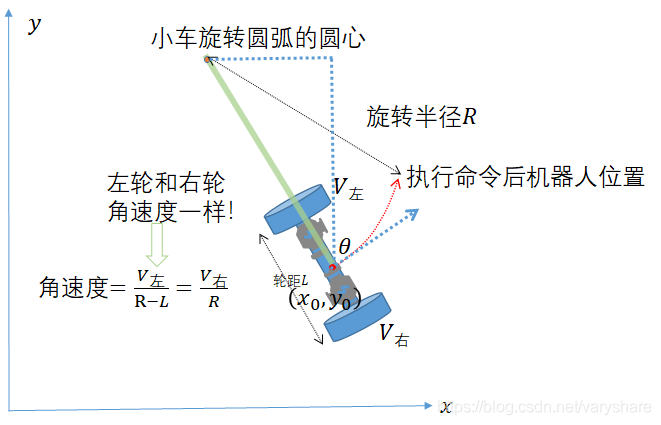
可以看到左轮速度和右轮速度不一样，它们之间差速会使得j机器人会作一个圆弧形旋转。而由于两个轮子都在同一个旋转半径上，所以角速度一样。虽然我们不知道旋转半径R是多少但是我们知道两个轮子的角速度一样，那么有下面这个等式。

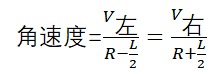
而上等式我们除了R不知道外，其他所有变量都是知道的。所以可以解出旋转半径R。

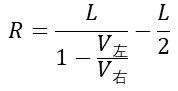
现在圆弧轨迹的旋转半径求出了那么旋转的轨迹，执行命令后的机器人位置和朝向都是已知的了。
我们现在已知执行命令前机器人位置为$(x_0,y_0)$，正面朝向与y轴正方向夹角是$\theta$。从下图可以看出机器人的圆弧轨迹的圆心坐标为:


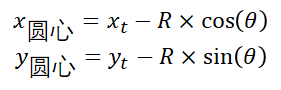
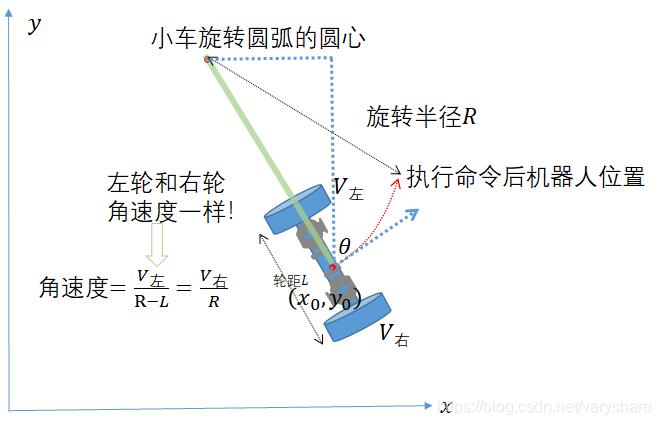
注意：当左右两个轮子速度一样时是不会发生旋转的即“机器人是做直线运动”也就没有圆弧这一个概念。
现在我们知道机器人的圆弧轨迹的圆心坐标为:

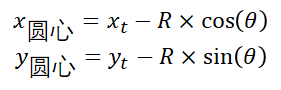
现在又知道圆的半径R为了知道命令执行后机器人所在的位置还得求在时长为t的这段时间内圆弧对应的圆心角。而角速度乘上时间t就得到这段时间内机器人转过的角度也就是圆弧对应的圆心角。

我们可以将某个时刻的机器人速度分解成x方向和y方向两个方向的速度

因此在时刻t机器人的位置可以通过积分来求得：



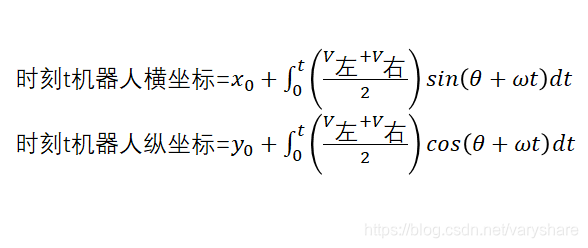
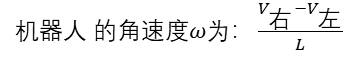
所以整理上面几个式子可得：

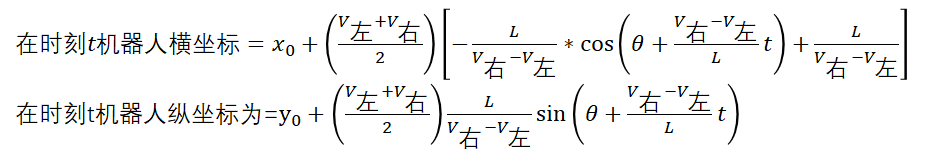
当左右两个轮子速度一样时机器人保持直线行驶：

化简可得：

Python编程模拟差速驱动

# -*- coding: utf-8 -*-
"""
Created on Fri Aug 23 15:18:57 2019
差速驱动的python实现
@author: 李韬@Ai酱
https://blog.csdn.net/varyshare/article/details/100042079
"""
from math import sin,cos
def diffdrive(x, y, theta, v_l, v_r, t, l):
    """
    模拟两个轮子的机器人执行差速驱动控制命令
    :param x,y 当前机器人位置
    :param theta 当前机器人朝向
    :param v_l 左轮速度控制命令
    :param v_r 右轮速度控制命令
    :param t 当前命令持续时间
    :param l 两个轮子的宽度
    :return: 执行命令后机器人到达的位置x_t,y_t
    和它的朝向theta_n
    """
    
    # 1. 先计算机器人朝向角度变化，右轮相对左轮作圆周运动
    # 只有两个轮子之间的差速会改变机器人朝向
    d_v = v_r - v_l
    omega = d_v/(l/2) # 机器人朝向变化角速度
    d_theta = omega *  t
    theta_t = theta + d_theta
    
    
    # 2. 计算t时刻机器人位置
    if v_l == v_r:
        x_t = x + t*(v_l + v_r)/2*sin(theta)
        y_t = y + t*(v_l + v_r)/2*cos(theta)
    else:
        x_t = x + (v_l + v_r)/2 * (-l/d_v*cos(theta + d_v/l*t)+l/d_v)
        y_t = y + (v_l + v_r)/2 * (l/d_v) * sin(theta + d_v/l*t)
    pass

    return x_t, y_t, theta_t