易懂的机器人理论与实践(2): 机器人移动模型建模（Motion model）Python代码编程实现

本文未经知乎@Ai酱许可，禁止转载

注意：本文提到的机器人移动模型仅限于带轮子的这种机器人，不是几条腿的那种。

很多滤波算法（如贝叶斯滤波，卡尔曼滤波）需要根据机器人移动模型和测量值来融合估计机器人当前所在的位置。什么是滤波算法？这里的滤波算法是指从有噪声的机器人位置数据中估计出机器真实位置。据移动模型可以依据控制命令对机器人现在所在位置和姿态进行估计，也就是说根据移动模型可以得到机器人位置和姿态的一个粗略估计值。然后使用滤波算法将移动模型输出的这个粗略的机器人位姿估计值和传感器（如GPS，陀螺仪）实际测量值融合就可以得到精确的机器人位置和姿态的估计值。那什么是移动模型，给定上一个机器人位置信息，再给定一个控制命令，通过一系列公式计算得到执行命令后机器人预期位置。这里面的“一系列公式计算”就是移动模型。在你实现一个滤波算法前需要先对机器人进行移动模型建模（即建立机器人的移动模型）。本文会介绍两种常见的机器人移动模型建模，分别是：基于里程的移动模型，和基于速度的移动模型。
你可能还是不大理解移动模型与滤波算法以及传感器测量值之间的联系。我画两张图你就懂了。
下面这张图就是用移动模型计算出机器人（蓝点，身体朝向是水平向右）执行某个指令后5000种可能的位置（红点，可以看到在中间那块是最有可能的，使用移动模型计算一次机器人位置就根据位置描一个点，一共计算了5000次）。它控制命令是逆时针转90度然后向上走一段距离。下面这个根据移动模型计算出的图其实就一个概率分布。

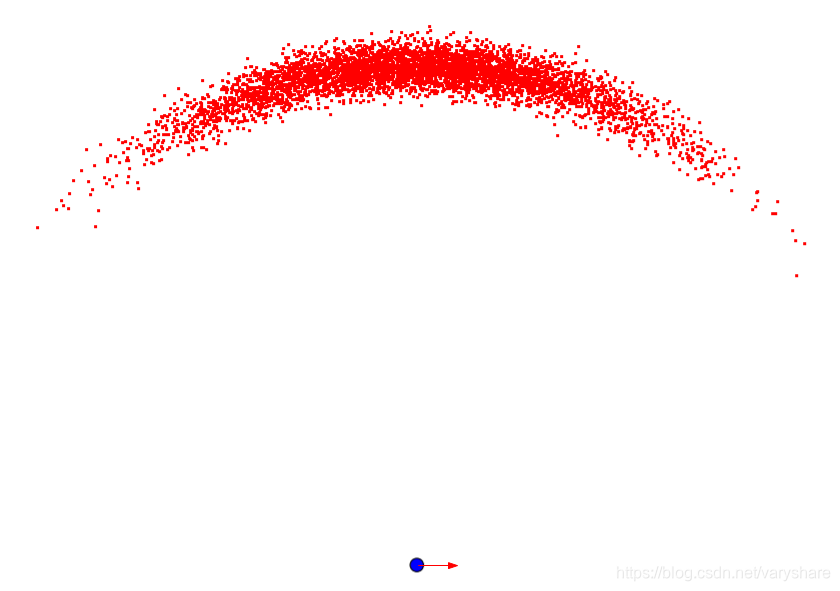
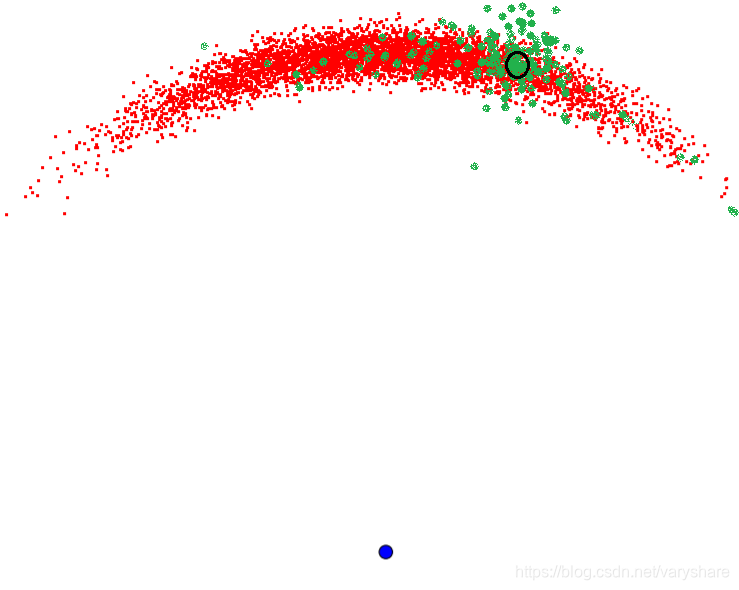
那么滤波算法是怎么融合移动模型得出的粗略估计值和传感器测量值的呢？看下面这个图。绿色是传感器多次测量的测量值。然后发现黑色圈是绿色和红色都很密集的地方。那么滤波算法就认为当前机器人位置精确估计就在黑色圈那个地方。

基于里程的机器人移动模型(Odometry-based Motion Model)

什么是里程？咱们坐出租车就知道里面有个里程计。这个里程计可以统计轮胎转了多少距离。所以我们可以直观的理解里程就是某个指标的一段变化量大小。这个变化量可以指距离变化也可以指角度变化。

注意了：基于里程的机器人移动模型要解决的问题是在已知机器人上个时刻位置和朝向角度、已知上个时刻到现在时刻这段时间内机器人预期移动距离和角度变化，的情况下求当前时刻机器人所在的位置和朝向。举个例子看看移动模型做了什么事。已知上个时刻机器人位置坐标是(1,0)，这段时间变化量是(0.1,0.2)；移动模型会计算当前时刻机器人的位置估计: (1,0)+(0.1,0.2)+(一个随机数,一个随机数)。

你一定会有三个问题：

• 问题零，机器人移动模型到底有什么用？答根据移动模型可以依据控制命令对机器人现在所在位置和姿态进行估计，也就是说根据移动模型可以得到机器人位置和姿态的一个粗略估计值。然后使用滤波算法将这个粗略的估计值和像GPS这样的传感器实际测量值融合就可以得到精确的机器人位置和姿态的估计值。
• 问题一是我怎么就知道上个时刻到现在这段时间预期机器人移动了多少和预期朝向变化了多少。关于这个问题我答案是这个根据控制模型算出来的。什么是控制模型？就是输入控制命令和机器人的位置信息控制模型就能告诉我机器人执行命令后预期会走多远身体朝向变了多少。你感兴趣的话可以看看这篇文章机器人理论与实践(1): 差速驱动原理与python编程模拟 （控制模型建模））。
• 问题二是直接把上个时刻的位置加上这段时间位置变化量不就是当前时刻的位置么？这个非常正确。但是由于命令在执行过程中总会有误差，所以还需要再加上一个很小的噪声。加上噪声后它就可以更接近机器人的实际执行过程（因为移动模型就是需要根据控制命令，尽可能准确的估计执行命令后机器人实际位姿）。也就是说上个时刻机器人位置坐标是(1,0)，这段时间变化量是(0.1,0.2)；移动模型会这么计算当前时刻机器人的位置估计: (1,0)+(0.1,0.2)+(一个随机数,一个随机数)。

从上面的描述可以看到怎么根据控制命令生成噪声随机数是移动模型中的关键。比如机器人某条命令是：转30度，直走2m，再转-20度。那么这三个命令就得执行三次，那就得加3次噪声随机数。移动模型大致讲完了。剩下的就是具体怎么科学的加噪声。在前面提到的两种常见的机器人移动模型建模，分别是：基于里程的移动模型，和基于速度的移动模型。这他们两最大区别也是在于加的噪声不同。

举个例子介绍下基于里程的移动模型的细节（和前面讲的差不多，主要是怎么加噪声的细节）：
假如是机器人初始位置是(0, 0)朝向与x轴正方向是0度，然后控制命令是“逆时针转90度，再直行1m”。在前面提到了每执行一步操作就加一次噪声。所以移动模型会这么做：
步骤1： 机器人逆时针转90度。真正执行时候转过的角度（里程）可能就是90+噪声1随机数。那么它朝向角度估计值就变成了执行前角度+当前命令转动角度+噪声=0+90+高斯噪声随机数1。用代码表示就是0+90+random.normal(0,方差1)
步骤2： 机器人直行1m。真正执行的时候走过的距离估计值（里程）是1+噪声2随机数。用代码表示就是0+1+random.normal(0,方差2)。注意这是斜着走的 。所以我们需要根据步骤1中的机器人朝向角度算出机器人在x和y方向各个方向走的距离（里程）才能得到机器人执行命令后的坐标估计值。横坐标：x=上个时刻机器人横坐标+机器人执行命令后斜着走的距离估计值*cos(执行上个操作后机器人朝向角度)=0+(1+噪声2随机数)*cos(0+90+高斯噪声随机数1)。纵坐标：y=上个时刻机器人纵坐标+机器人执行命令后斜着走的距离估计值*sin(执行上个操作后机器人朝向角度)=0+(1+高斯噪声2随机数)*sin(0+90+高斯噪声随机数1)。

现在只有高斯噪声随机数1和高斯噪声随机数2是未知的。由于噪声的均值是0，所以我们需要确定他们的方差是多少。其实非常简单就是让方差与里程呈正比就可以。很容易理解转动角度越大当然噪声的不确定性（方差）越大，走的距离越远噪声的不确定性也应该增加。
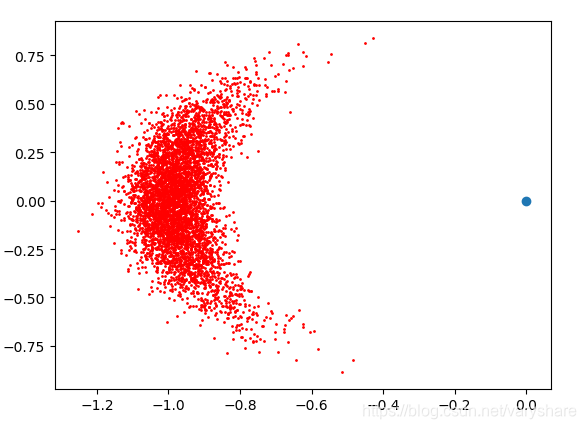
下面是这段文字的代码实现（基于里程计的机器人移动模型github代码地址）

# -*- coding: utf-8 -*-
"""
https://blog.csdn.net/varyshare/article/details/100061173
@author: 知乎@Ai酱
"""
import numpy as np
def odometry_motion_model():
    # 机器人初始位置
    (x,y,theta) = (0,0,0)
    """
    机器人控制命令：
    1. 转90度
    2. 直行1米
    """
    theta_cmd = np.pi/2
    distance_cmd = 1
    
    # 机器人移动模型
    scale_factor1 = 0.09 # 用于调节机器人转动操作的噪声大小
    theta_predict = theta + theta_cmd + np.random.normal(0, scale_factor1*theta_cmd)
    
    scale_factor2 = 0.03 # 用于调节机器人直行操作的噪声大小
    distance_predict = distance_cmd + np.random.normal(0, scale_factor2*distance_cmd)
    x_predict = x + distance_predict*np.cos(theta_predict)
    y_predict = y + distance_predict*np.sin(theta_predict)
    
    return x_predict,y_predict

x_arr = []
y_arr = []

for _ in range(5000):
    x_predict,y_predict = odometry_motion_model()
    x_arr.append(x_predict)
    y_arr.append(y_predict)
    
import matplotlib.pyplot as plt
plt.scatter(0,0)
plt.scatter(x_arr,y_arr,c='r',s=1)
plt.show()

基于速度的移动模型

一般基于速度的移动模型里面有两种速度：旋转速度和平移速度。一般商用机器人也会提供相应的速度控制接口。基于速度的移动模型和上面的基本一样。唯一的区别就是基于里程计的是里程需要加噪声误差，而基于速度的移动模型是速度需要加噪声误差而已。
python代码实践

# -*- coding: utf-8 -*-
"""
https://blog.csdn.net/varyshare/article/details/100061173
@author: 知乎@Ai酱
"""
import numpy as np
def velocity_motion_model():
    # 机器人初始位置
    (x,y,theta) = (0,0,0)
    """
    机器人控制命令：
    1. 旋转速度0.1弧度/s , 持续时间2s
    2. 直行1米/s，持续时间1s
    """
    rot_velocity, rot_time = np.pi/2, 2
    trans_velocity, trans_time = 1, 1
    
    # 机器人移动模型
    scale_factor1 = 0.09 # 用于调节机器人转动速度的噪声大小
    d_theta_predict = (rot_velocity+np.random.normal(0, scale_factor1*rot_velocity))*rot_time
    theta_predict = theta + d_theta_predict
    
    scale_factor2 = 0.06 # 用于调节机器人直行速度的噪声大小
    distance_predict = (trans_velocity+np.random.normal(0, scale_factor2*trans_velocity))*trans_time
    x_predict = x + distance_predict*np.cos(theta_predict)
    y_predict = y + distance_predict*np.sin(theta_predict)
    
    return x_predict,y_predict

x_arr = []
y_arr = []

for _ in range(5000):
    x_predict,y_predict = velocity_motion_model()
    x_arr.append(x_predict)
    y_arr.append(y_predict)
    
import matplotlib.pyplot as plt
plt.scatter(0,0)
plt.scatter(x_arr,y_arr,c='r',s=1)
plt.show()

总结

基于里程的移动模型一般比基于速度的移动模型要更准确。因为里程信息可以在执行完控制命令后直接从轮子那读取。但是速度的话并不能像里程那样精确用传感器获取。当然里程信息也有缺点，它等到执行完才能知道机器人走了多远距离。而速度信息可以在控制的时候就确定，比如控制命令是当前机器人保持1m/s速度直行3小时。所以使用里程和速度信息进行机器人移动建模各有优缺点。基于里程的移动模型适合在机器人行走过程中估计机器人的位置信息（执行命令后）。基于速度的移动模型适合用于运动规划避碰（执行命令前）。