推荐开源项目:简单的SLAM与机器人教程与编程实践-github
我们在做几何变换的时候经常需要把某个坐标系上的所有点都进行一个旋转,这个操作就叫做刚体旋转(所有的点相对位置不变的发生旋转)。下图是一个典型的二维坐标系下刚体旋转。我们把蓝色的坐标系旋转了θ度,新坐标系就是红色的坐标系。我们现在已知一个点相对红色那个坐标系的坐标(xred,yred),和已知旋转角度θ,然后我们想求得该点相对于蓝色那个坐标系的坐标(xblue,yblue)。
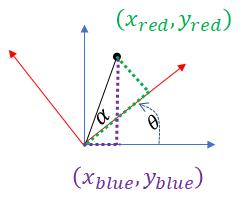
这个其实很简单我们利用高中学的三角几何就可以轻松解决。从上图可以发现不变量是黑色的那个线段的长度。而这个长度我们是可以根据黑色点相对红色坐标系下的坐标(xred,yred)算出来的。黑色线段长度为r=xred2+yred2.
然后我们可以根据紫色那个三角形计算出黑色点相对蓝色坐标系下的坐标(xblue,yblue)。
根据高中学的三角几何我们可以知道:
xblue=r∗cos(α+θ)yblue=r∗sin(α+θ)
现在这个α我们是不知道的。但是我们能找到一个关于它的线索。
xred=r∗cos(α)yred=r∗sin(α)。
为了用上这个线索我们需要对下面这个式子进行展开。
xblue=r∗cos(α+θ)=r∗(cos(α)∗cos(θ)−sin(α)∗sin(θ))=xred∗cos(θ)−yred∗sin(θ)yblue=r∗sin(α+θ)=r∗(sin(α)∗cos(θ)+cos(α)∗sin(θ))=yred∗cos(θ)+xred∗sin(θ)
所以我们把上面那个式子总结成向量相乘的方式那就是:
xblue=[cos(θ),−sin(θ)][xred,yred]T
yblue=[sin(θ),cos(θ)][xred,yred]T
然后可以进一步整理成矩阵相乘的形式:
[cos(θ)sin(θ)−sin(θ)cos(θ)]




