贝叶斯公式在机器学习中有什么用,实例讲解Python实现朴素贝叶斯分类器
贝叶斯公式=贝叶斯定理
贝叶斯公式到底想说啥
贝叶斯公式就是想用概率数学来表示事件发生依赖关系。
贝叶斯公式长下面这样:
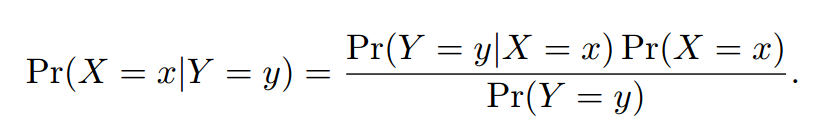
用图形怎么表示贝叶斯公式
就是X的面积。
就是Y的面积。
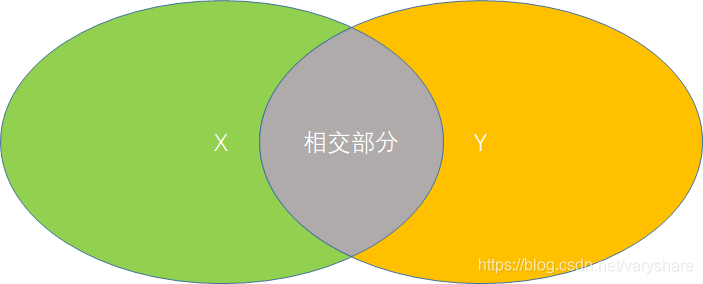
是什么?是指Y发生的情况下X发生的概率。用图形表示就是,只看Y的情况下Y里面的X占比多少。这不就是相交部分除以Y的面积么?相交部分计算方式=X的面积*相交部分占X的比率。
再看看前面的公式就完全能理解了。
朴素贝叶斯分类器
任何机器学习都是要套一个数学模型。那朴素贝叶斯分类器套的是什么模型呢?
它是想计算一个概率值。什么概率呢?就是当样本为x时,这个样本来自类A的概率是多少,来自类B的概率是多少。如果来自类A的概率>来自类B的概率。那就分类器输出样本属于类A。
用公式表示就是P(A|x)>P(B|x)=》x属于A .其中P(A|x)表示当样本取值是x时它来自类A的概率,P(B|x)表示当样本取值是x时它来自类B的概率。
这样咋看好像很有道理的样子。那么问题来了,我咋知道样本x属于A和B的概率,要我知道了那还用分嘛?
接下来看,如何计算样本取值为x时属于A的概率P(A|x)、和属于B的概率P(B|x)(下面一段话很重要一定要仔细看,没弄懂不要往后看)
根据贝叶斯公式我们知道。其中P(A)表类A占比总数据中的比例。P(x)是指样本值等于x的数据占总数据的比例。P(x|A)表示在类A中,有多少个和x一样的数据。这三个概率我们都是知道的。那么或许你会问前面只有一个特征,那两个特征的样本怎么计算概率?答:假设一个样本有两个特征x,y。那么。计算P(B|x)和计算P(A|x)同理。
举个例子:
数据格式为
(样本值x,样本值y,类标签)
(1,0,A)
(0,1,A)
(1,1,B)
(0,0,B)
如果我们想知道样本(0,1)是属于类A的概率有多大,我们得先计算下这几个概率值:P(A),P(0,1|A),P(0,1)。
- ,
这个指的是标签为A的数据占总数据中的比例 - ;其中指的是样本(0,1)占总数据中的比例是多少,这道题中我们直接可以看出来是,但是有些情况下无法直接统计和样本值完全相同那就得用公式计算了。其中指的是样本第一个特征等于0的数据占总数据中的比例。其中指的是样本第二个特征等于1的数据占总数据中的比例。我们通过计算出来的值和我们直接观察到的(0,1)占总数据比例是相等的,都是证明我们计算没有问题。
- ; 用乘法公式计算P(0,1|A)。你或许会发现明明P(0,1|A)就是等于嘛,为何用乘法公式计算出来是。这是因为乘法公式的前提是特征x和特征y时相互独立的。而在本例中乘法公式失效是因为在类A中的数据两个特征x,y是明显是相互干扰,x=1那么y不是1。通过举例子是想告诉大家,贝叶斯分类器它默认的前提是各个特征他们是相互独立的,这个特征的取值不会影响另一个特征的取值。其实主要原因是我们为了方便说明数据量太少所以不独立很正常,只有数据量足够大才能表现出独立性。
Python编程实践贝叶斯分类器
# -*- coding: utf-8 -*-
"""
贝叶斯分类器实现逻辑异或
@author: @Ai酱
"""
import numpy as np
#数据格式[特征x,特征y,标签]
data = np.array([[1, 1, 'B'],[1, -1, 'A'],[-1,1, 'A'],[-1, -1, 'B']])# 注意:当Numpy的ndarray有不同类型同时存在时它们会转换为字符串
label_index = 2
feature_num = 2
def counter(feature_index,value):
return float(np.count_nonzero(data[:,feature_index]==str(value)))# 注意:当Numpy的ndarray有不同类型同时存在时它们会转换为字符串
def P_label_x(label,x):
'''
计算P(label|x)的概率
label取值:'A','B'
'''
# 计算p(x=(x1,x2...))=p(x1)*p(x2)*...
p_x = 1
for i in range(feature_num):
p_x = p_x * (counter(i,x[i])/data.shape[0])
# 计算p(label)
p_label = counter(label_index,label)/data.shape[0]
# 计算p(x|label)=p(x1|label)*p(x2|label)*...
p_x_label = 1
data_is_label = data[data[:,label_index]==label]
for i in range(feature_num):
num_xi_in_label = np.count_nonzero(data_is_label[:,i]==x[i])
p_x_label = p_x_label * (num_xi_in_label/data_is_label.shape[0])
pass
# 计算p(label|x)=(p(x|label)*p(label))/p(x)
p_label_x = (p_x_label*p_label)/p_x
return p_label_x
def bayes_classifier(x):
'''对样本x进行分类'''
p_A_x = P_label_x('A',x)
p_B_x = P_label_x('B',x)
if p_A_x>p_B_x:
return 'A'
else:
return 'B'
pass
print(bayes_classifier(np.array([-1,1])))
贝叶斯公式在机器学习中有什么用?答参数估计
答:用于参数估计。机器学习做的事情其实就是找到一个概率分布函数,输入一个数据输出是这个数据属于某个类的概率。
那么怎么找这个概率分布函数呢?一般是默认是高斯分布。
下面是用贝叶斯公式估计逻辑回归里面的参数过程
假设样本的概率分布是高斯分布。高斯分布长下面这样,有两个参数。贝叶斯公式就是用来估计这两个参数。
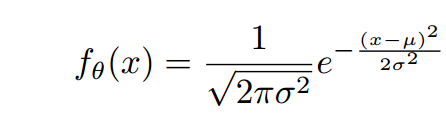
那么贝叶斯公式怎么估计这两个参数你呢?将记作为。也就是说我们需要估计的值是多少。
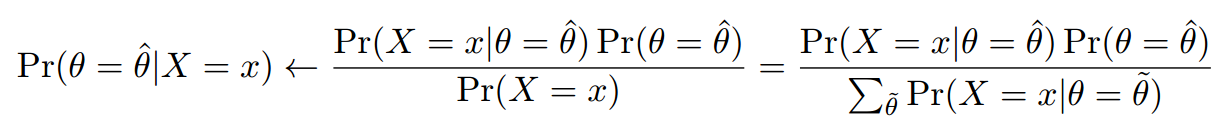
其中。上面那个公式的意思就是说,有很多很多取值,是其中一个。那么怎么知道哪个最好呢?计算是X的最好参数的可能性,哪个可能性最大就选哪个参数。这就是极大似然法。,极大似然法就是现有有多个可能的参数取值,我不知道取哪个最好。为了知道取哪个最好。我要计算出各个参数为优参数的可能性。然后将可能性最大的那个参数作为目前的概率分布函数最优参数。
那假如取值无限种情况呢?
取值无限的情况下,需要用梯度下降优化极大似然法这个等式.下面这个等式。不懂梯度下降可以看看这两篇文章:
https://www.zhihu.com/question/305638940/answer/670034343
https://blog.csdn.net/varyshare/article/details/89556131
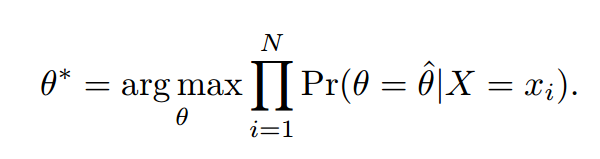




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· Java 中堆内存和栈内存上的数据分布和特点
· 开发中对象命名的一点思考
· .NET Core内存结构体系(Windows环境)底层原理浅谈
· C# 深度学习:对抗生成网络(GAN)训练头像生成模型
· .NET 适配 HarmonyOS 进展
· 本地部署 DeepSeek:小白也能轻松搞定!
· 如何给本地部署的DeepSeek投喂数据,让他更懂你
· 从 Windows Forms 到微服务的经验教训
· 李飞飞的50美金比肩DeepSeek把CEO忽悠瘸了,倒霉的却是程序员
· 超详细,DeepSeek 接入PyCharm实现AI编程!(支持本地部署DeepSeek及官方Dee