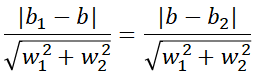通俗解释高中生能听懂的SVM本质和原理

当年SVM怎么被发明的？

任何机器学习都是套一个数学模型，然后求解数学模型的待求解参数。SVM使用的是怎样的一个模型呢？。现在把我们作为一发明者，看看下面这张图。知道一个算法原理最好的方法是研究它是怎么想出来的，不然直接看公式可能马上就记住了，但是过了段时间就会忘因为没有理解。
如果是下面这张图，我们怎么划分开这两组数据？最简单的方式就是用一条直线。现在我们已经发明了一种算法（事实上别人已经发明了，这种用一条直线划分开两组数据的算法叫做线性回归）。

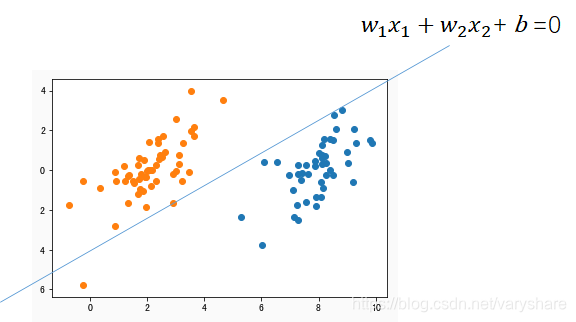
既然一条直线能解决这个分类问题为何别人还要想发明其他算法呢？我们看看用一条直线划分数据进行分类这个算法的缺点。我们看上面那个图和下面这个图有什么区别？这两个图都能实现将两个数据划分开。但是上面那个图的直线，总是看起来很别扭好像差了点什么。我们还是比较喜欢下面这种直线。

那下面这个图的直线有什么特征呢？怎么用数学量化这个特征呢？又如何指导算法让算法尽可能的选下面这种直线作为划分界线呢？解决这三个问题这就是SVM发明的初衷

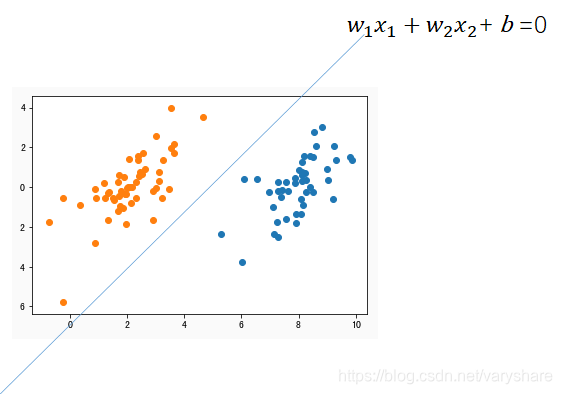
用来划分两个分类的更好的直线有哪些特征？如何量化这些特征？

我们对比前面两张图，我们会发现那个直线刚刚好就在数据中间。而不会贴着数据边缘。那么直线不会贴着数据边缘这句话怎么用数学来量化呢？
用理工科的思维就是问：
1. 边缘是什么？
2. 怎么量化直线与边缘的距离？
答：边缘是指两个类中离直线最近的那些点；由于边缘是点。那么量化边缘与直线之间的距离那就非常容易了（用高中学到的点到直线间的距离公式）

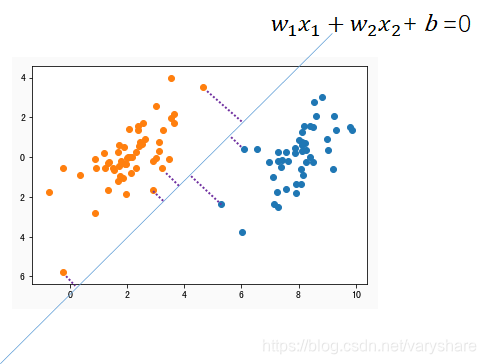
SVM发明者就是想最大化两个分类的边缘到直线的距离。好像是那么回事，但是边缘有很多点算距离还是很麻烦啊。那SVM发明者到底怎么解决这个问题的呢？

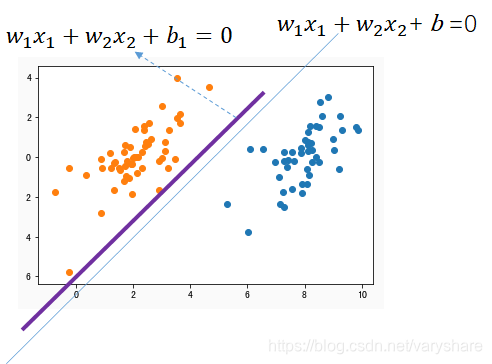
答：把直线平移（斜率不变改变截距），平移到第一次和左边那个某个点相交（平移后的那个直线是下图紫色直线）。这之间平移的距离不就是界线（蓝色那条直线）与橘黄色分类的边缘之间的距离么？

下面我们看看怎么计算橘黄色那个类边缘到分界直线的距离。其实这个距离就是紫色直线与蓝色直线的距离。用高中老师教的两平行直线间的距离公式为：

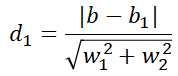
复杂的算法当初的想法往往就是这么简单粗暴，由于每个算法都会经历几十年的发展，所以后面这些人把前面那些人的这些简单的想法汇总在一起那就变成了一个复杂的算法了。同样的我们也可以计算边界线与另外一个类边缘的距离。
下面图是我们将直线平移到两个分类的边缘的效果图。

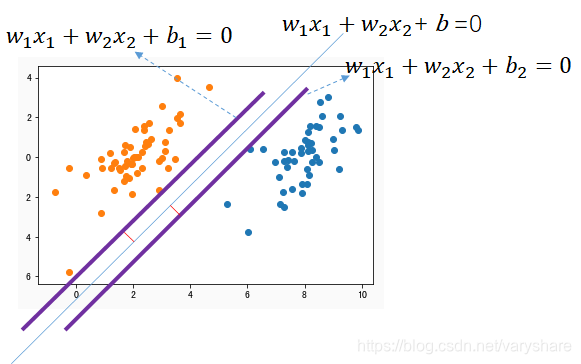
事实上，我们只需要让平移后的那两条紫色直线之间的距离尽可能大就可以了。然后分界线就取两条紫色直线的中线即可尽可能的和两个类的边缘远了。

两条紫色直线的距离用高中老师教的两平行直线距离公式可以表示为：

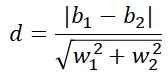
所以我们要不断的调整$b_1,b_2,w_1,w_2$这四个值（在保证这两条直线能将两堆点划分开的情况下），尽可能的让上面那个距离公式$d$更大。
那么还有个问题疑团，“在保证这两条直线能将两堆点划分开的情况下”这句话怎么用数学量化？
答：

把上面那几句话表示成下面这个公式，就是我们经常看到资料介绍SVM的公式了：

细心的你会发现好像和传统的SVM公式有那么点细微的差别。那么差别在哪呢？我写的公式里面没有 +1和-1。
这其实也是前人发明者的一个技巧，当时别人就在想。列的公式还要区分那个点是属于橘黄色那个类还是蓝色那个类，这太麻烦了。我能不能把那个两个不等式合成一个不等式？
我们再分析下这三条直线距离的关系。

如果是蓝色分界线是两个紫色的中线那么意味着它到两个紫色的线距离相等。也就是说下面这个公式成立。

而这个公式分母相等，就分子不同。所以我们让分子相同即可.我们只用保证$\frac {b_1+b_2} 2 =b$即可，那为何我们不这样设计$b_1=b-1, b_2 =b+1$呢(从截距看有$b_1<b_2$的)？
我们看看这样设计有什么好处。我们凑出来

1. 如果$(x_1,x_2)$是橘黄色的点那么有：
   $w_1x_1+w_2x_2+b-1>=0$
2. 如果$(x_1,x_2)$是蓝色的点那么有：
   $w_1x_1+w_2x_2+b+1<=0$

一推导得到：

1. 如果$(x_1,x_2)$是橘黄色的点那么有：
   $w_1x_1+w_2x_2+b>=1$
2. 如果$(x_1,x_2)$是蓝色的点那么有：
   $w_1x_1+w_2x_2+b<=-1$
   那我能不能用 变量y表示点的所属分类。其中y=1表示橘黄，y=-1表示蓝色？这样我把两个式子可以合并成这样（你将两种情况代入看是否成立）：
   $y*(w_1x_1+w_2x_2+b)>=1$也就是$1-y*(w_1x_1+w_2x_2+b)<=0$

于是我们得到了传统的SVM目标函数的公式，待确定参数$w_1,w_2,b$

$max\rightarrow \frac 2 {\sqrt {w_1^2+w_2^2}}$
并且$\rightarrow1-y*(w_1x_1+w_2x_2+b)<=0$

其中y是坐标$(x_1,x_2)$所属分类。当$(x_1,x_2)$是橘黄色那就y=-1，当$(x_1,x_2)$是蓝色那就y=+1。上面那个分子是2怎么得到的？答：$b_1=b+1, b_2 =b-1,所以 b_1-b_2=2$。
上面那个公式看起来有点小别扭，就是 $w_1和w_2$在分母里面，我们能不能把它弄出来。其实非常简单，我求分数的最大值，不就是求分母的最小值嘛。上面那个公式变成了：

$min \rightarrow {w_1^2+w_2^2}$
并且$\rightarrow1-y*(w_1x_1+w_2x_2+b)<=0$

现在目标函数我们得到了，那怎么根据目标函数来算出比较好的$w_1,w_2和b$？那个不等式怎么处理？

一般是这么处理，其中C是一个常数。这个处理方法叫做拉格朗日对偶（高中没学过也没关系这是凸优化里面的内容）。从直观理解也可以很容易理解的。左边的w越小两条紫色的直线距离越大，但是越大没用啊他们会无限大。还得让这两条直线能夹在两堆数据中间。右边那个部分就是用来调整两条直线尽可能的保持在数据的中间。那个C就是用来调节两条直线多靠拢。C（比如无穷大）太大了会导致右边那个数占比非常大，会导致两条直线靠太拢（对新来的数据容易误判）。C太小（比如0）会导致右边那个部分不起作用，导致两条直线无限远（容易误判数据）。
$min \rightarrow {w_1^2+w_2^2}+C*(1-y*(w_1x_1+w_2x_2+b))$
接下来那就是用梯度下降来求解这个最小值时候对应的参数$w_1,w_2,b$。不懂梯度下降？看这个通俗讲梯度下降是什么
梯度下降迭代更新这三个参数的方法：
$w_1 = w_1 - 学习率 * 对w_1的导数 = w_1 - 学习率 * (2w_1-Cyx_1)$
$w_2 = w_2 - 学习率 * 对w_2的导数 = w_2 - 学习率 * (2w_2-Cyx_2)$
$b = b - 学习率 * 对b的导数 = b - 学习率 * (-Cy)$

python 实现

import numpy as np
epoch = 500
w = np.array([np.random.rand(),np.random.rand()]) #初始化[w1,w2]
b = np.random.rand()
for _ in range(epoch):
    for i in range(x.shape[0]):
        xi = x[i]
        labeli = label[i]

        learning_rate = 0.01
        c = 0.6 #超参数
        w = w - learning_rate*(2*w+c*labeli*xi)
        b = b - learning_rate*(c*labeli)

def classifier(x):
    result = np.matmul(x,w)+b
    result[result*(-1)-1<0]=1
    result[result*1-1<0]=-1
    return result

classi_result = classifier(x)