从本质看决策树，谈谈信息熵是怎么发现的,ID3决策树Python实践实现XOR异或

本文首发于CSDN @Ai酱 的博客，转载请注明出处。

任何机器学习的套路

机器学习算法看起来那么多，其实套路就一个。那么多算法是背不下来的，自己知道他们怎么根据套路想出来的就可以。
套路就三步：

1. 选取一种数学模型来对数据进行分类预测*。线性回归是用直线这个数学模型来划分数据。逻辑回归是用sigmoid这个函数来输出一个概率值。决策树是想用一个二叉树来对数据分类（二叉树也是一个数学模型）
2. 确定一个评估模型的指标。这是我们通常讲的目标函数。为何要确定评估模型的指标呢？因为第1.步所选取的数学模型它有未知参数的，这个未知参数得我们自己根据训练集来计算出来。那么我咋知道未知参数到底取值是多少是最好，这就需要一个评估指标。一般评估指标是长这样$(\hat y - y)^2 /N$，这个评估指标描述的是各个点和模型之间距离的平均值。还有其他的评估指标。像逻辑回归和决策树就是用概率来评估参数好不好，什么概率呢？，就是当前所设定的参数把输入的数据所属分类预测对的概率。
3. 根据2.中的评估模型来遍历找让评估指标达到最高的参数。如果可以遍历那就遍历，如果参数是无法遍历那就用梯度下降（或者其他反正是用来求比较好的参数的）。其实有时候找到不一定是最好的参数，但是能用。差不多就行。就像你开车，没必要精确转方向盘转到16°，你只需要转到差不多就够了。

决策树的本质

决策树本质就是想在每个特征上找一个阈值，根据这些阈值来对数据分类。这个阈值是通过遍历来找到的。
比如：
我想根据{年龄，身高，体重}来判断一个人性别{男，女}。
给模型输入的数据长这样：

{年龄，身高，体重，标签}
{10，100，60，男}
{45，155，110，女}
{21，171，114，男}
... ...

然后决策树是这么做的：
剩下没确定阈值特征们 = {年龄，身高，体重}。
只要剩下没确定阈值特征们不为空。那么就遍历剩下没确定阈值特征们的特征。
下面是遍历的过程：

• 现在我取出年龄这个特征，为了找到一个年龄划分点（根据年龄区别男女）。我得遍历所有年龄。从1~125岁遍历（因为人最最多活125岁，最小我认为是1岁。这个你可以自己设定多少的。）。比如现在我猜测10是划分点。那么我认为大于10的是男人，小于10的是女人。我还可以猜20岁是划分点，猜32岁是划分点。那么哪个划分点是最好的呢？后面会讲，这个要根据评估指标计算取让评估指标最高的那个作为实际的划分点。每设定一个划分点计算一次评估指标。。（是不是很有意思？后面会讲怎么评估划分点好不好的指标）
• 取出身高这个特征。然后找身高划分点。从20~260cm（身高也就这个范围）遍历划分点。遍历过程举例小于150cm认为是女，大于150认为是男。小于151cm认为是女，大于151cm认为是男…就这样每设定一个划分点计算一次评估指标。
• 体重同上
  然后，这三种特征的每个划分点对对应一个评估指标值。指标值最大的情况作为第一次划分。现在你不用关系评估指标是什么你只需要知道每种划分情况都可以计算一次评估指标值。举个例子：

(所取特征，划分点） 评估指标
...
(年龄,10岁)               0.5
(年龄,11岁)               0.39
(年龄,12岁)               0.51
...
(体重,120斤)               0.6
(体重,121斤)               0.61
(体重,150斤)               0.4
(体重,190斤)               0.3
...
(身高,160cm)              0.8######评估指标最大#######
(身高,120cm)              0.7
...

可以看到(身高,160cm) 0.8这个划分方法让评估指标最大，然后我们就选他。这是第一层划分。因为决策树它是树嘛，所以是分层来的。现在身高的阈值已经确定是160cm了。把现在的决策树用个图形表示就是下面这样子：

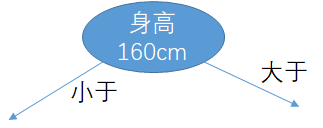
现在剩下没确定阈值特征们 = {年龄，体重}。
遍历各种情况。重复上面那个过程，选选一种划分方法，让评估指标最大。直到所有的特征都确定划分点的阈值。当然现在出现新的情况。身高有个两个分支。到底哪个分支好？还是遍历，选择让评估指标最大的那种情况。比如是下面这个情况：

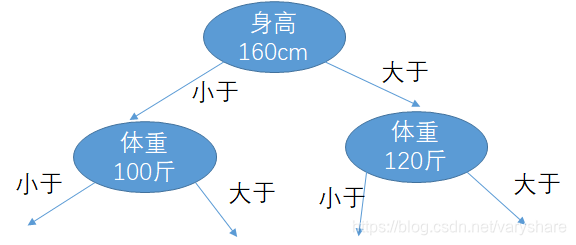
现在确定了体重的阈值，接下来就要确定年龄的阈值。反正都是遍历，取让评估指标最大的那个情况。

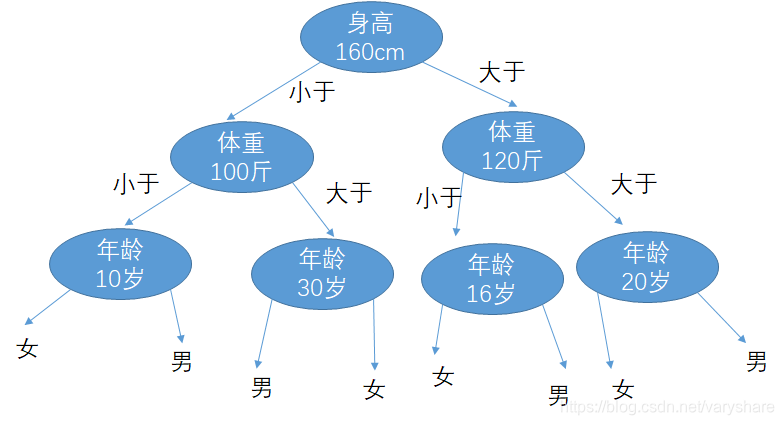
上述过程仅仅是本人用于说明决策树的过程的用途。里面数据是用于假设性说明不针对任何人群

ID3算法构造决策树评估指标到底是什么？

答：当前所设定的参数所确定的模型 它会将数据进行划分，划分后的数据的混乱程度就是评价指标。这个混乱程度叫做信息熵。混乱程度听起来像那么回事，具体是什么下面会解释。ID3全称什么根本不重要，重要的是如果你出生早很多年，知道用混乱程度评估决策树模型好不好说不定也可以想到这个方法。知道原理就可以。

什么是信息熵

关于博主思考信息熵这个概念的思路过程（有时候知道怎么想出来的比知道是什么更重要）看这篇文章<遇到问题，有哪些有效的分析方法？>
答：是衡量信息混乱程度的数学指标。什么叫做混乱？什么叫做不混乱？我举个例子：
一个袋子有10个球。如果红球5个白球5个这叫做混乱，如果红球9个白球1个这叫做不混乱。从直观理解就是如果各种东西比例都一样那么我想判断这个袋子里面有什么东西就比较困难，所以叫做混乱。如果这个袋子只有一种东西，那么我判断这个袋子里面有什么东西就很容易，这叫做不混乱。总结：一个集合里面各部分比例越均衡越混乱，各部分越两极分化越不混乱。我们要想把数据分类那就越不混乱越好。比如我把标签为男的数据都划分到一个集合，那判断一个样本它是分类成男还是女不就很简单了。
那怎么用数学来衡量混乱程度呢？ 我们找找规律，看下面这个发现什么规律没有？加起来相同的情况下，把两种球数目相乘的数越大越混乱，越小越不混乱。那么是不是我们可以用这个相乘的结果来衡量数据混乱程度？当年香农就发现了这个规律，然后写了它第一篇研究生论文（woc原来这么简单其实你早出生也可以写出来的，香农最牛逼的不是发现这个，而是它根据这个进行泛化然后衍生出来一门新学科《信息论》。可以发现牛逼的学科往往起点是很简单的，最关键是专注于这个方向进行演化出新学科）。：

10个球，它可以有这些情况：
5+5    =======> 5*5=25     最混乱（很均衡）
4+6    =======> 4*6=24     次混乱
1+9   =======>  1*9=9       不那么混乱
0+10 =======>  0*10 = 0    最有序（两极分化）

一般我们是用占比来相乘而不是数量相乘（其实反正都一样）。

• 如果这个袋子不止两种球还有很多种球怎么办？一样的，把他们占比连乘。
• 但是连乘有个缺点：不好求导。比如$f(x)*g(x)$我想对这个求导，它得用乘法求导规则展开。所以大家一般喜欢把它变成加法。怎么变？取对数，因为对数单调递增所以不会影响原先数值的单调性的，原先x大的现在的函数值仍然大。
• 取对数也有个缺点ln(x)确实是单调增的，但是x不能为0啊。x是占比，范围是[0,1]。所以x是可以取0的。当x=0时，ln(x)没有意义它的极限是负无穷。我能不能让0乘这个负无穷呢让它变成0呢？于是就衡量混乱程度的指标就变成了$xln(x)$，x单调增，ln(x)单调增。所以乘起来还是单调增。原先x大的现在的函数值仍然大。而当$x \rightarrow 0$时，$x*ln(x)=0$

总结： 信息熵=各个部分的占比乘在一起的结果值*ln(各个部分的占比乘在一起的结果值)=x*ln(x)

举个例子说明信息熵在决策树中起的作用

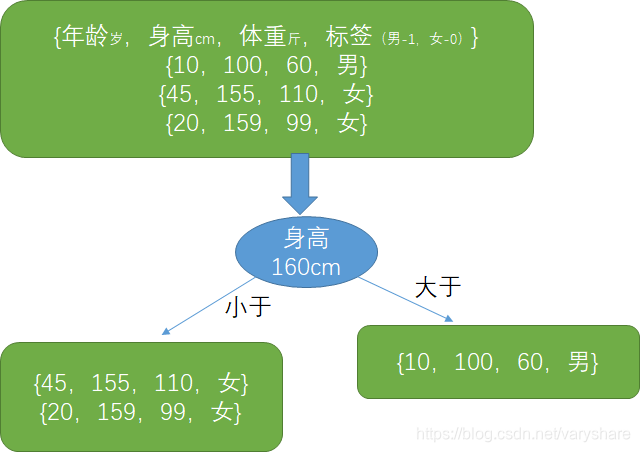
某次划分如下所示，我们看看他们的信息熵有没有变化（各个部分占比相乘的数值大小有没有变化）。现在这次划分方法是：“身高这个特征，划分点的阈值是160cm”。这个把原先的训练集划分成了两部分，这使得原先很乱的数据变得有一点点有序了（这个叫做熵减，高中化学应该听过）。
划分前：男女比例分别是：1/3和2/3.
划分后：男女比例：左子集$\frac2 3 * [\frac 0 2 , \frac2 2]$ 和 右子集$\frac1 3 * [\frac1 1 , \frac 0 1 ]$。左子集要乘个$\frac 2 3 *$表示的是左子集占整个集合的比例是$\frac 2 3$. 右子集要乘个$\frac 1 3 *$表示的是右子集占整个集合的比例是$\frac 1 3$.

划分前：信息熵=$ln(\frac 1 3 * \frac 2 3)=ln(\frac 2 9)$
划分后：信息熵=$(\frac2 3 * \frac 0 2 * \frac2 2 * \frac1 3 * \frac1 1 * \frac 0 1)*ln(\frac2 3 * \frac 0 2 * \frac2 2 * \frac1 3 * \frac1 1 * \frac 0 1)=0$
所以我们看到，当前这个划分还不错。直接就达到了最优的划分。让数据变得最不混乱。你可以尝试计算其他划分情况下的信息熵，你会发现都会比当前这个划分的信息熵大。

信息熵计算

import numpy as np
# 计算信息熵，p是当前这个类别占整个集合的比例
def entropy(p):
    if p==0:
        return 0
    else:
        return -p * np.log2(p)

当只有两个分类时，占整体比例有一个是1另一个是0.这是最理想的。此时提供的信息最大，因为我只要从集合里面取那就一定是第一个分类的物体。而当两种物体占比都是0.5和0.5的时候提供的信息最小。

根据ID3规则进行决策树 实现电路逻辑XOR异或功能实践

import numpy as np
# 决策树实现异或XOR，相异为True，相同为False.
# 数据格式[特征1，特征2，标签]
data = np.array([[1, 1, False],[1, 0, True],[0,1, True],[0, 0, False]])
label_index = 2 # 标签所在列


features_num = 2 # 特征的数量
features_possible_value = np.array([[0,1],[0,1]]) #各个特征可能的取值
features_use_info = np.array([False,False]) # 各特征是否已被用来划分数据

def split_set(dataset,feature_index, border_value):

    # 按照指定特征的指定值划分数据集。
    # 划分方法：左子集是指定特征小于等于指定值，右子集是指定特征大于指定值
    left_set_index  = dataset[:,feature_index]<=border_value
    right_set_index = dataset[:,feature_index]>border_value

    return dataset[left_set_index], dataset[right_set_index]

# 计算信息熵，p是当前这个类别占整个集合的比例
def entropy(p):
    if p==0:
        return 0
    else:
        return -p * np.log2(p)

#计算集合的熵
def entropy_dataset(dataset):
    if dataset.shape[0]==0:
        return 0
    # 先计算两种类别的数据的占比
    p_true = (dataset[:,label_index]==True).shape[0]/dataset.shape[0]
    p_false = 1.0 - p_true #（由于只有两个分类所以可以这么算）
    return entropy(p_true) + entropy(p_false)


def make_tree(count,root_data):
    min_entropy_recorder = {}
    #count: 序号，记录是第几次划分
    min_entropy_recorder[count]={'entropy':np.inf}# 记录各种划分方法下的最小的熵和对应划分方法
    tmp_data = root_data

    # 如果数据已经都是一个类了那就不用再划分了
    if np.alltrue(tmp_data[:,label_index]==True):
        return 0,{} #已经都是一个类就熵是0，不用做任何划分动作
    
    #如果特征用完了,只用返回熵，不用做任何动作
    if np.alltrue(features_use_info) or count>features_num:
        return entropy_dataset(root_data),{}

    # 1. 遍历剩下没有使用的特征
    for tmp_feature in np.nditer(np.where(features_use_info==False)):
        # 2. 遍历当前特征各种取值情况
        tmp_values = features_possible_value[tmp_feature]
        features_use_info[tmp_feature]=True
        for v in np.nditer(tmp_values):

            # 3. 按照当前特征的选定值将现在的集合划分为两个子集
            left_set,right_set  = split_set(tmp_data,tmp_feature,v)
            #递归的划分新的子集
            entropy_left, left_recorder = make_tree(count+1,left_set)
            entropy_right, right_recorder = make_tree(count+1,right_set)
            select_child = ''
            # 哪个子集划分的熵最小就选哪个子集作为划分方案
            if entropy_left<entropy_right:
                select_child = 'left'
                min_entropy_recorder.update(left_recorder)
            else:
                select_child = 'right'
                min_entropy_recorder.update(right_recorder)

            # 计算左子集和右子集占总集合的比例
            left_rate = left_set.shape[0]/tmp_data.shape[0]
            right_rate = right_set.shape[0]/tmp_data.shape[0]
            entropy_all = left_rate*entropy_left + right_rate*entropy_left
            
            # 如果当前划分方法是目前最好，那就记录当前的划分方法和熵
            if min_entropy_recorder[count]['entropy']  > entropy_all:
                min_entropy_recorder[count]['entropy'] = entropy_all
                min_entropy_recorder[count]['feature'] = tmp_feature
                min_entropy_recorder[count]['border']  = v
                min_entropy_recorder[count]['select_child']  = select_child
                pass
            pass
        features_use_info[tmp_feature]=False #回溯
        pass #end循环
    return min_entropy_recorder[count]['entropy'], min_entropy_recorder
    pass # end函数


print(make_tree(0,data))

(0.0, {0: {'entropy': 0.0, 'feature': array(0, dtype=int64), 'border': array(0), 'select_child': 'right'}})

你的赞是我愿意知识分享的的动力
其他机器学习推荐资料：
https://zhuanlan.zhihu.com/p/59678480
https://zhuanlan.zhihu.com/aitom
https://zhuanlan.zhihu.com/p/64010777
https://zhuanlan.zhihu.com/p/60539567