4分钟看懂逻辑回归是什么？要优化什么参数？和极大似然法有什么关系？机器学习小总结

文章末尾对机器学习的规律总结。机器学习这么多算法记住是很难的，如果懂别人怎么想到这个算法的那就容易多了。学习机器学习一定不要死记。记住别人怎么想到这个算法以及各个概念之间的联系，各个方法有什么用，这些最重要。本文就是从还原算法怎么想到的角度来讲而不是纯粹推导，解释了各个概念之间的联系。

逻辑回归到底是什么？要优化什么参数？为何要优化这些参数？

逻辑回归它输入是样本，输出是样本输入某个类的概率。逻辑回归只能分类出两种类，是一个二分类算法。也就是说$f(x)$输出是属于类A的概率。那么如果某个样本不属于A呢则它属于B的概率是$1-P(A)=1-f(x)$。因为逻辑回归输出的是A的概率$即f(x)=P(A)$。逻辑回归里面它认为模型是一条曲线。这条曲线的函数长下面这样，其中$w,b$是我们要设置的参数。选择一种$w,b$相当于我们假设了一种模型。

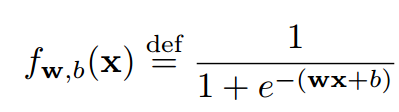
比如$w=2,b=1$那么将$w=2,b1=$代入进去，就变成了。这样的取值可以有很多很多，没选择一种取值就假设了一种模型。那么哪种是最好的呢？这个问题就变成了，$w,b$到底是多少才是最好。$w,b$这就是我们要优化的参数。

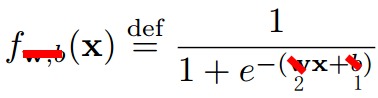
逻辑回归和线性回归最大区别地方有两个

• 一 是线性回归它认为模型是一条直线，逻辑回归它认为模型是一条曲线。
• 二是优化参数的方法。线性回归就是想让各个样本点离画出来的直线的平均距离尽可能短。而逻辑回归则不是算平均距离。它是用概率来优化的。优化方法叫做极大似然法。还是不懂要优化什么参数？和怎么优化的？看下面的：

极大似然法怎么优化逻辑回归的参数的？

$f(x)$的输入是一个样本，输出是这个样本属于各个类的概率。假设这个样本属于A类，那我是不是希望模型$f(x)$输出的概率中认为样本属于A类的概率越大越好？换句话说就是，$w,b$各种可能的取值对应各种假设的模型。能让模型认为样本属于A类的概率最大的那种情况的参数是最好的，这就是极大似然法的动机。

极大似然法优化逻辑回归的原理？

我们选择了$w,b$的一种可能的取值然后确定了一个模型$f(x)$。现在有N个样本，输入到模型$f(x)$。那么会有N个值，这N个值表明了这些样本属于样本A的概率。他们同时发生的概率就是这些概率相乘。

这些样本都是自己有标签的。我们希望模型输出来他们属于它标签的那个类的概率尽可能的大。这个想法就是极大似然法的想法。那么现在问题来了，模型计算他们属于它标签的那个概率？
答：模型输出都是样本属于A的概率。逻辑回归只能分出两种类，要么是A要么不是A。现在我们知道了样本属于A的概率，那么样本属于B的概率=样本不属于A的概率。
举个例子：$f(样本1）=0.1$，然后样本1的标签是B，那么模型计算出来样本属于B的概率是$1-f(样本1）=1-0.1$。

我们模型认为样本属于A或B来计算概率的分成两个公式，这个很麻烦。
能不能一个公式就能算出来默认认为样本属于它所在那个表标签的概率。
于是就有了下面这个公式，有两个类一个是1另一个是0. 样本的标签是$y_i$。当样本属于1的时候，$1-y_i=0$意味着后面那个式子等于1也就是没有了。当样本属于0的时候，$y_i=0$意味着前面面那个式子没有了。

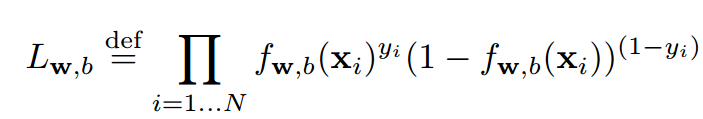
上面这个式子就是我们假定的$w,b$下模型计算出各样本属于他们标签的概率。我们要做的是不断改动$w,b$，找到一个让上面那个式子最大的$w,b$。这就是极大似然做的事。根据概率找最优的参数。
那怎么找呢？用梯度下降。梯度下降不理解可以看看这个知乎回答，非常推荐：如何理解梯度下降。本文主要是为了打破一些概念性的障碍，让你对这些概念之间的联系有了解。如果你想学习梯度下降实践可以看看这篇文章 适合初学者的神经网络理论到实践(1): 神经网络实战：单个神经元+随机梯度下降学习逻辑与规则 。
由于连乘不好计算导数（对连乘求导要用到乘法求导法则很麻烦），所以一般是消掉连乘。两边取对数就可以消掉。而且log是单调增，它最值点还是和原先最值点一样。所以求得的最优参数和原先的解是一样的。

神经网络和逻辑回归的关系？

答：逻辑回归就是神经网络中的一个神经元。

机器学习小总结

其实机器学习算法看起来很多事实上本质上就是 假设数据符合某个模型+建立误差模型+梯度下降求解未知。

我谈谈自己的看法吧：

1. 线性回归：它假设数据是一条直线。然后误差模型是各个点和直线之间的距离平均值要最短。然后用梯度下降求解直线的斜率和截距。
2. 逻辑回归：它假设数据是一条"S"曲线，输入一个样本输出它属于某个类的概率，只能分出两个类。然后误差模型是通过概率来算的。它尝试参数各种可能的情况，然后选择能让模型计算出样本属于它标签的那个类的概率最大。比如样本1标签是A，模型计算出样本1属于A类的概率是f(样本1),那么我就要调整模型的参数使得f(样本1)尽可能的趋近于1. 让这个概率尽最大的那个参数是最优参数。得到最优参数就得到了一个"S"曲线。这就是我们的模型。
3. 决策树 ：它假设数据可以用if else这样的树状结构来分类。然后也是根据概率来求树的结构是怎样的。
4. SVM:它假设数据可以用两条直线划分开来。和线性回归很像。然后让这两条直线尽可能区分开数据，并且这两条直线距离尽可能的远。优化的参数就是两条直线斜率和截距。求解最优参数还是梯度下降。
5. 可以看到，机器学习套路一般是先假设数据可以被哪种模型区分开，然后建立一个模型。然后用梯度下降求解模型中未知参数的最优解。

你的赞是我愿意知识分享的的动力

[1] 知乎专栏《适合初学者的神经网络机器学习入门理论到实践》
[2] 知乎人工智能、机器人专注初学者教程答主 Ai酱