{高中生能看懂的}梯度下降是个啥?
刚接触机器学习的同学避不开的一个专业名词就是梯度下降。顿时心里万马奔腾,其实很简单的,你先得理解概念才能看到那些公式不怂。(当然本文全程无公式,书写用时2小时,阅读估计10分钟)

本文主要解决三个问题:
- 梯度到底是啥?
- 梯度下降有啥用?
- 为啥要下降?
问题一:梯度是个啥?
其实“梯度”你Ctr+H替换成“导数”就可以了,梯度就是目标函数的导数。以后你在书上遇到这个词就替换成“导数”就容易理解多了。
至于Gradient为啥翻译成梯度,我也不知道,知道的朋友告诉下我涨下姿势。>_>
问题二:梯度下降有啥用?
用问题一的解决方案,替换“梯度”为“导数”。问题变成了:导数下降干嘛的?
我暂时把答案写上稍后解释:梯度下降就是用来求某个函数最小值时自变量对应取值。这个函数名字叫做损失函数(cost/loss function),直白点就是误差函数。一个算法不同参数会产生不同拟合曲线,也意味着有不同的误差。损失函数就是一个自变量为算法的参数,函数值为误差值的函数。梯度下降就是找让误差值最小时候算法取的参数。(看到这里肯定也是一脸懵逼,马的好不容易知道梯度是啥现在又tmd多了个损失函数,不急看完损失函数是啥再回头看就懂了梯度下降干嘛的了)
那么什么是损失函数(误差函数)?
机器学习算法中有一类算法就是产生一条曲线来拟合现有的数据,这样子就可以实现预测未来的数据,这个专业术语叫做回归(见到回归就替换成拟合就好了^)。还有另外一种类似也是产生一条曲线,但是这个曲线时用来将点分隔成两块,实现分类,在这个曲线一侧为一类另外一侧算一类。
但是我怎么知道这个算法产生的拟合曲线效果好不好呢?这个东东叫做误差,预测值减去真实值最后取绝对值,没错就是这么简单粗暴~~
产生的拟合曲线并不是完全和现有的点重合,拟合曲线和真实值之间有一个误差。一个算法不同参数会产生不同拟合曲线,也意味着有不同的误差。损失函数就是一个自变量为算法的参数,函数值为误差值的函数。梯度下降就是找让误差值最小时候这个算法对应的参数。(是不是突然感觉好像知道了梯度下降干嘛的了,今日宜赞、收藏(要赞不要脸->-))
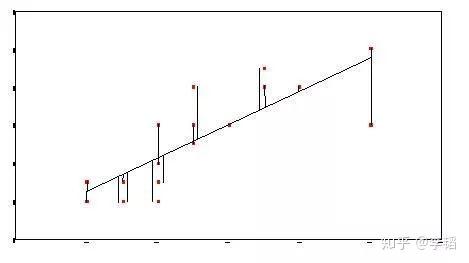
直线为拟合曲线周围的点是现有的数据(图片来自网络侵删)
问题三:梯度为啥要下降?
你如果能回答这个问题基本看书上梯度下降一些公式就清楚很多了。
解:依题意可得
翻译问题。☞按照问题一的解决方法可知:我们将“梯度为啥要下降?”这个问题翻译为:找误差函数最小值所对应的自变量,为啥要让导数的绝对值变小。我们看下图这个二次函数对应曲线就是误差函数(也就是损失函数,一般是叫损失函数,误差函数是我为了好理解说的),自变量是算法的参数,函数值是该参数下所产生拟合曲线与真实值之间的误差值。注意了,注意了,注意了:一般你看到梯度下降的公式最好想到下面这个图,对就假设误差函数就这么特殊,都是开口朝上,都是平滑的,都是只有一个导数为0的点,都是弯一下而不是弯很多下。
自变量是算法的参数,函数值是该参数下所产生拟合曲线与真实值之间的误差值。
2. 平常我们怎么求损失函数(误差函数)最小值?☞我们目标是求这个损失函数(误差函数)最小值时候对应自变量的值,也就是求曲线最低点自变量x的取值。用高中知识怎求最小值?老师说了求最值不要怂,上来求个导,然后让导函数为0时候取最值。告诉你还真就可以这么干的,简单粗暴。不过这个方法不是梯度下降,它有个很高端大气上档次的名字叫做正规方程(Normal Equation),吓到了吧这么简单的原理居然名字这么高端,所以嘛梯度下降也差不多就名字吓人而已。但是为啥这么简单粗暴容易理解,为啥还要用梯度下降呢?因为一般来说越简单粗暴的方法效率越低~,正规方程在数据量大时候太慢了,就像冒泡排序那么简单为啥排序算法一般不用冒泡排序一样。敲重点了>>>梯度下降和这个原理类似见下面
- 梯度下降怎么求损失函数(误差函数)最小值?☞假如你拿着手机地图不用导航去找一个目的地怎么走?我一般是往某个方向走一段路程,然后发现好像离目的地近了,然后产生一个想法“这个方向能使得我离目的地距离更小”,然后我继续沿着这个方向走。(你就会疑问该不会梯度下降就这么做的吧,没错就是这么做的)。
注意了,注意了,注意了:一般你看到梯度下降的公式最好想到下面那个图,对就假设误差函数就这么特殊,都是开口朝上,都是平滑的,都是只有一个导数为0的点,都是弯一下而不是弯很多下。(哈哈怕你记不得,复制粘贴一遍)
想象下:
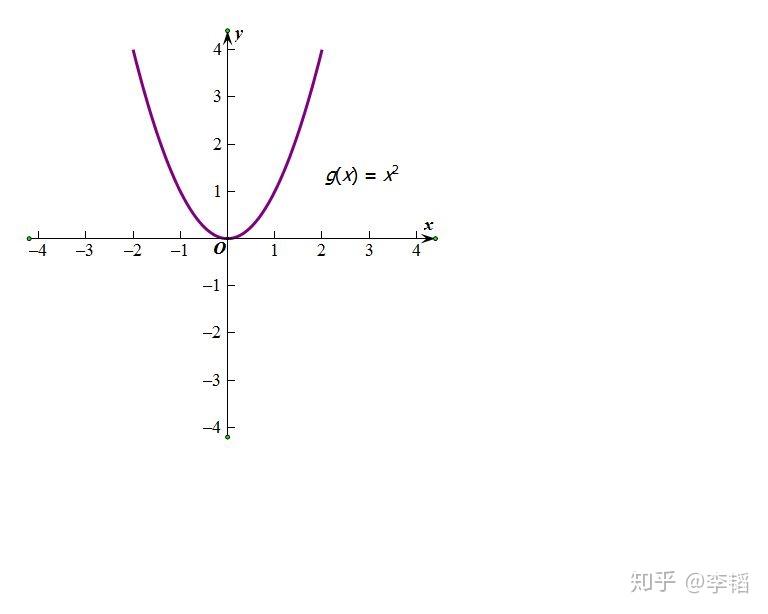
按照上面那个图的特点,假设这个图放大1万倍,大到你不能一眼看到最小值。那么要你找最小值对应的自变量x,你怎么找??记住我们目的是为了找自变量x,记住我们目的是为了找x
你将可能会在电脑屏幕看到原先那个图的局部,按照它们单调性来分主要有这三种情况
情况1:单调下降,导数为负(梯度为负)

情况2:单调上升,导数为正(梯度为正)

情况3:基本看到了最小值,,导数很接近0(梯度很接近0)
当你遇到情况1:单调下降,导数为负(梯度为负),要想找到函数的最小值所对应的自变量的值(曲线最低点对应x的值)怎么走?当然是水平向右滑啦,也就是让x增大,此时随着x增大,导数(梯度)的绝对值是减小的(梯度下降含义懂了吧哈哈就这个意思)
当你遇到情况2:单调上升,导数为正(梯度为正),要想找到函数的自变量的值(曲线最低点对应x的值)怎么走?当然是水平向左滑啦,也就是让x减小,此时随着x减小,导数(梯度)的绝对值是减小的(也就是梯度下降)。
综上所述:
梯度就是导数
梯度下降作用是找到函数的最小值所对应的自变量的值(曲线最低点对应x的值)。记住我们目的是为了找x.
梯度下降含义(具体操作)是:让改变x的值使得导数的绝对值变小,当导数小于0时候(情况1),我们要让目前x值大一点点,再看它导数值。当导数大于0时候(情况2),我们要让目前x值减小一点点,再看它导数值。当导数接近0时候,我们就得到想要的自变量x了。也就是说找到这个算法最佳参数,使得拟合曲线与真实值误差最小。(理解这段话,就不用硬背公式啦)



