啤酒与尿布？挖掘商品之间的关联性分析(1):机器学习之Apriori算法

从这个贸易战看：强权即是真理，没有所谓的自由贸易和平等。中国之大已容不下一个安静的键盘。不过是又一次鸦片战争。除了愤怒还是愤怒，除了一心想为崛起而澎湃还是一心想为崛起而澎湃。中华文明三四千年的历史都是世界顶级，美国人区区100多年第一就想再占100年这不是无知么？中国人有13亿人，是美国人的4倍还要多，4个抵1个也是必然会超过美国。
2019年5月29日 IEEE宣布禁止任何受华为资助的教授或学生参与IEEE审稿。听到这个消息我是愤怒的，说好的科学无国界呢？
梳理下这个过程：
2018.12.1，华为CFO（任正非之女）被美国下令逮捕
2018.12.1 对芯片重大贡献的华人张首晟在美国身亡，就在2年前获得中国国家科学技术奖（中国科技最高奖，最高领导人亲自颁奖，奖金200万美金）
2019年5月 美国撕毁两国元首已经基本确定的协议，对中国征收25%关税。
2019年5月中旬 美国禁止全世界任何企业与华为接触或者提供设备，也禁止购买华为手机或通讯设备。理由：“国家安全”(距离美国棱镜门用思科通讯设备和Google监听全世界这个事件不过几年美国人就忘了自己干了什么事。)同时禁止欧洲其他国家使用华为提供的5G服务。
2019年5月中下旬，Microsoft,ARM,Google纷纷宣布停止和华为任何商业来往，同时Google禁止华为手机使用Google服务。
2019年5月底， IEEE（世界上最大电子电气学术机构）禁止任何受华为资助的教授参与审稿。禁止其他高校或企业与中国的一些高校合作。

1. 背景

一个广为流传的挖掘商品之间的关联性的故事就是“啤酒与尿布”这个故事。相传某超市通过分析顾客的账单，发现啤酒总是和尿布一起购买。通过分析，发现这是因为美国人喜欢喝啤酒，当买尿布的时候看到啤酒就顺便买了。于是就把啤酒与尿布总是放在一起卖。这样的有关联性的商品还有很多。如洋葱和土豆捆绑消费等等。将关联度高的商品放在一起促销或者捆绑消费可以提高营业额。同时电商平台也可以捆绑推荐提高成交量。而当商品非常多的时候，人工已经无法分析出众多商品的关联性。这个时候就需要计算机辅助人们找到哪些商品是经常被一起购买。目前有众多分析商品关联性的算法，Apriori算法就是其中一个师祖级算法。很多都是由Aporiori算法演化而来，如下一篇挖掘数据关联性的文章<挖掘数据关联性(2): FP-growth算法>。当然Aporiori还有其他的应用场景。

2. 从本质看Apriori算法原理

2.1 算法要解决的问题是什么

要解决的问题：根据一堆账单数据，统计出哪些商品组合是高频率。
举个例子：如给出下面这些数据，希望算法能分析出“啤酒+尿布”这个组合是高频率。也希望它能分析出“西红柿+鸡蛋”也是高频率：

{啤酒 鸡蛋 尿布 西红柿}
{香烟 尿布 瓜子 啤酒 }
{土豆 西红柿 洋葱 醋 鸡蛋}

2.2 算法思路

最简单的方式是遍历所有商品组合情况，然后统计各种组合出现的频率。设定一个值只要出现频率大于这个值，我们就认为是高频。但是，如果有上百种商品。那么组合的数量就非常巨大了。粗略用高中学的知识算下去单单100种商品就有10的30次方种情况。对于普通计算机来说超过10的6次方这个数量级就已经很慢了。所以直接遍历各种组合然后统计各种组合出现的频率肯定不行。那么人们开始想到我们能不能排除一些情况。把它的数量级降很多。这就是Apriori算法的初衷。

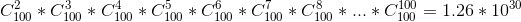
那么问题来了怎么排除一些组合情况呢？这还是得回到我们需要解决什么问题上面来。我们要解决的是统计经常出现的那些组合。那么我们只需要排除那些肯定不是高频率的组合即可。
那么什么样子的组合是肯定不是高频率？答：“含有很少见的那种组合的那个组合肯定不是高频率”。这句话有点拗口，我举个例子。
现在我们知道“人参+尿布”是一种频率非常低的组合，那么“人参+尿布+燕窝”肯定也是频率非常低。为什么呢？要是“人参+尿布+燕窝”这个组合的频率高，肯定意味着“人参+尿布”肯定是高频率组合（因为“人参+尿布+燕窝”包含“人参+尿布”这种情况）。

于是我们可以确定筛除规则：如果某个组合出现频率非常低，那么所有包含这种组合情况的组合出现频率也非常低。我们可以直接不统计这些组合出现频率。举个例子：我们知道“人参+尿布”出现频率低，那么我就不会统计任何包含“人参+尿布”的组合了。也就是说“人参+尿布+燕窝”，“人参+尿布+土豆”，“人参+尿布+洋葱+花生”这些情况他们肯定是低频率，可以不用统计。

上面提到的那个筛除规则，就是Apriori的筛除规则。接下来就是要确定如何量化某个组合是否是高频率。

2.2.1 某组合出现频率量化指标

指标1: 包含某个组合的账单记录占总账单记录的比率
从直观上评价{啤酒+尿布}这个组合的频率就是看包含{啤酒+尿布}这个组合的账单记录占总账单记录比率。看下面这个数据。包含{啤酒+尿布}的记录条数是3条，总记录条数是4，那么{啤酒+尿布}这个组合的频率就是3/4。在Aporiori算法中，人们把这种频率计算方式叫做支持度(support）。

{啤酒 鸡蛋 尿布 西红柿}
{香烟 尿布 瓜子 啤酒 }
{土豆 西红柿 洋葱 醋 鸡蛋}

上面那个指标这样根据组合占所有账单的比例来计算频率会存在某个问题。就是某些商品本来就出现频率低。如{人参+燕窝}，这个可能是一个强关联的商品组合。但是这个组合占总的账单记录比率一定很低。因为平常很少有人买的。但是只要买了{人参}的人很可能会顺便买{燕窝}。那么怎么解决这个问题？这就要引入下面这个指标。

指标2：出现{人参+燕窝}的记录数占出现{人参}的账单记录数的比率，这种评估频率的方式叫做可信度或者叫做置信度(confidence)
如何评估各种组合出现频率已经介绍完了，接下来介绍下Aporiori算法的具体步骤。

2.3 Apriori算法具体步骤（在本文中暂时只把指标1作为衡量某个组合出现的频率）

• 第一步肯定是要设定多大才是高频率。比如设定支持度（指标1）>=0.5那就认为是高频率。这个到底多大才是高频率你可以根据实际情况改。
• 然后要构造出各种情况的组合，然后在构造的过程中计算目前产生的组合的支持度。如果支持度<0.5那就认为出现频率低，根据前面提到的筛选规则。任何包含某个低频率的组合情况的组合都是低频率可以不进行计算。也即是说我计算出某种组合情况是低频率，那么我后面就不根据它来构造新的组合了。那么怎么构造各种情况的组合呢？答: 用两个队列，一个存上次的组合，另一个存心的组合。在构造的过程中，放弃低频率的组合情况（这个叫做剪枝）。以减少计算量。
• 返回所有高频率组合。
  以下面这个数据集为例。为了方便，我们给各个商品进行编号。
  [1]啤酒 [2]鸡蛋 [3]尿布 [4]西红柿 [5]香烟 [6]瓜子 [7]土豆 [8]洋葱 [9]醋

账单1：{啤酒 鸡蛋 尿布 西红柿}
账单2：{香烟 尿布 瓜子 啤酒 }
账单3：{土豆 西红柿 洋葱 醋 鸡蛋}

上面这个数据集用编号表示就是

[
[1, 2, 3, 4],
[5, 3, 6, 1],
[7,4,8,9, 2]
]

Aporiori统计高频率组合的方式是：

第一轮组合：

• 组合的结果是{1} {2} {3} {4} {5} … {8} {9}。
• 计算这9种组合的出现频率，然后剔除低频率组合。
• 含有组合{5}的记录占总记录比例=1/3.它是<0.5的。这意味着{5}是低频率组合，放弃用{5}进行下一步的组合。这意味着不会继续构造任何含有{5}的组合。除了{5}同样还需要剔除{6}{7}{8}{9}，含有它们的账单占总账单的比例均低于0.5
• 剩下的高频组合为：{1} {2} {3} {4}

第二轮组合：

• 组合的结果是：{1,2}{1,3}{1,4} {2,3} {2,4} {3,4}。
• 其中{1,2} {1,4} {2,3} {3,4}含有它们的账单占总账单的比例均低于0.5，所以剔除它们。
• 剩下的高频组合为：{1,3} {2,4}.

第三轮组合
… 略 …

Python实践：

# -*- coding: utf-8 -*-
"""
Created on Mon May 27 20:19:24 2019

@author: Ai酱
"""

import numpy as np
class Queue():
    val = np.array([])
    '''自己写个numpy队列'''
    def __init__(self,value=np.array([])):
        self.val = np.array(value)
    def size(self):
        return self.val.shape[0]
    def push(self,x):
        '''队尾增加一个元素'''
        self.val = np.append(self.val,np.array([x]))
    def pop(self):
        '''队头出队一元素'''
        if self.size()==0:
            return None
        else:
            last_elem = self.val[0]
            self.val = self.val[1:self.val.shape[0]]
            return last_elem

def count_freq(dataset, combinations):
    '''计算包含combinations各种组合的记录在dataset的占比'''
    freqs = np.zeros(len(combinations))
    for i in range(len(combinations)):
        combin_i=combinations[i]
        for item in dataset:
            if item.issuperset(combin_i):
                freqs[i] += 1
            pass
        pass
    pass
    # 计算比率
    freqs /= len(dataset)
    return freqs         

# 初始化
dataset = [
{1, 2, 3, 4},
{5, 3, 6, 1},
{7, 4, 8, 9, 2}
]
max_goods_id = 9 # 设置商品最大编号
qold = Queue(np.array([{i+1} for i in range(max_goods_id)]))
qnew= Queue()
high_freq = 0.5

# aporiori算法
for _ in range(3): # 最多只分析<=3种商品各种组合
    # 统计包含qold里面各种组合的记录的出现次数
    freq = count_freq(dataset,qold.val.tolist())
    # 只留下高频组合
    qold.val = qold.val[np.where(freq>high_freq)]
    print(qold.val)
    # 根据剩下的高频组合计算下次的组合
    qnew.val = qold.val
    qold.val=np.array([])
    
    while qnew.size()>0:
        tmpset = qnew.pop()
        for i in range(qnew.size()):
            qold.push(tmpset.union(qnew.val[i]))
    
'''
输出：
[{1} {2} {3} {4}]
[{1, 3} {2, 4}]
[]
'''