MIT18.06(7): 线性变换与JPEG图像压缩和小波基图像压缩,逆矩阵左逆与右逆和伪逆
线性变换
变换就是对一个向量进行平移旋转投影伸缩等操作。并不是所有的变换都是线性变换。
假设x是一个向量,T(x)表示对x进行变换。如果T(x)它满足下面这几个条件那么T(x)就是线性变换。下面这几个条件说了啥呢?它就是说我变换后的结果与变换前的结果它是成线性比的。
- T(x+y)=T(x)+T(y)
- T(cx)=cT(x)
- T(0)=0
这个T(x)其实和我们平时接触的函数是一样的,只不过它是对向量进行操作。T(x)它就是一种输入与输出的映射。
比如我们构造一个最简单的线性变换:T(x)=Ax,其中A是一个矩阵(类似我们平常常见的函数t(x)=3x)
任何向量都可以由坐标系中的基向量们的线性组合所表示,如下图所示。

线性变换在图像压缩中的应用
JPEG压缩算法,也就是我们平常经常见到的JPG文件。它的思想是把图像分成很多块。举个例子有一个512x512像素的照片,把它分成8x8的块,每块的大小为64x64像素.然后我们用几个基向量线性组合来表示各个块。于是乎,对于每个小块我们只需要保存线性组合的系数和基向量。这样就实现了图像压缩。在图像压缩中基向量到底取多少决定了压缩的效率,其中有一个比较出名的叫做傅里叶基。傅里叶基就是把傅里叶矩阵的列向量作为基向量。

用傅里叶基表示图像可以用公式来描述:其中是线性组合系数,是第i个傅里叶基(即傅里叶矩阵的第i行),是图像像素值。
如果直接用傅里叶基进行变换,这是无损压缩。那有损压缩是什么呢?前面提到了傅里叶基进行线性组合,那么线性组合的系数,这些数影响不大那么就可以舍弃。这样就产生的有损压缩。到底多小算小这就得设置一个阈值。设置这个阈值的原则是让我们肉眼看不出差异。
基向量除了可以用傅里叶基外还可以用小波基,小波基大概长这样。

小波基的好处在于各个列向量相互正交。这样求线性组合的系数方便。为啥咧?假设有一个向量它各个元素代表像素值,那么用小波基线性组合形式可以表示为:P=WC其中P是像素值,W是小波基矩阵,C是线性组合系数。由于W是小波基各个列向量相互正交,所以它是正交矩阵。正交矩阵有个性质就是。因此线性组合系数很容易就可以求出。
逆矩阵左逆与右逆和伪逆
当A不是方阵的时候就无法直接求逆矩阵。比如A是n×m这个就只能求左逆和右逆
- 左逆和右逆
就是A的左逆为何这么说?因为,所以是A的左逆。
就是A的左逆为何这么说?因为是投影矩阵投影到行空间。是把向量投影的列空间。,所以是A的右逆。 - 伪逆
啥时伪逆?就是当A不是方阵的时候让等于一个单位矩阵(不完全是单位矩阵就是左上角是单位矩阵其他地方是0)。
求伪逆的方法:
SVD分解求伪逆
如果你对SVD分解不了解可以参考这篇文章《SVD分解》
其中是对角矩阵(它不一定是方阵,U和V才是方阵)。
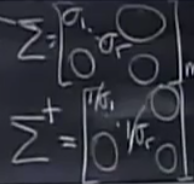
的伪逆是。如上图所示。
所以A的伪逆是,你可以拿它与乘起来看看是不是单位矩阵。



