优先级队列
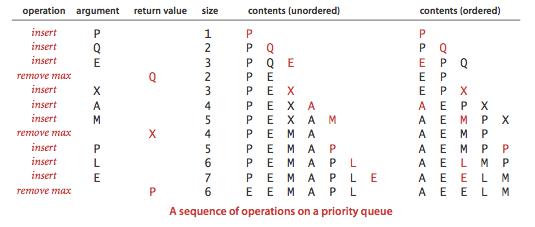
优先级队列的特征在于删除最大值和插入操作。
初级实现
- 数组实现(无序):惰性方法,仅在必要的时候找出最大元素;
- 数组实现(有序):积极方法:在插入时就保持列表有序,使后续操作更高效;
- 链表表示法
| 数据结构 | 插入元素 | 删除最大元素 |
|---|---|---|
| 有序数组 | N | 1 |
| 无序数组 | 1 | N |
| 堆 | logN | logN |
| 理想情况 | 1 | 1 |
| 在上述优先队列的初级实现中,删除最大元素和插入元素这两个操作之一在最坏情况下需要线性时间来完成。 |
堆的定义
1. 完全二叉树(从上到下,从左到右)
2. 一棵二叉树的每个结点都大于等于它的两个子结点时,它被称为堆有序
二叉堆表示法
如果使用指针来表示堆有序的二叉树,那么每个元素都需要三个指针来找到它的上下结点。
但使用完全二叉树,只需要数组而不需要指针就可以表示,十分方便。
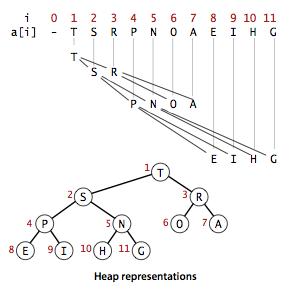
具体方法是将二叉树的结点按照层级顺序放入数组中。(下图_根节点从1开始)
| 位置 k | 父结点位置 | 两子结点位置 |
|---|---|---|
| 根节点从1开始 | k/2 | 2k,2k+1 |
| 根节点从0开始 | (k-1)/2 | 2k+2,2k+1 |
| 高性能的原因:利用在数组中无需指针即可沿树上下移动的便利。 |
堆的算法
我们在长度为 n + 1 的私有数组 pq []中表示大小为 N 的堆,其中pq [0]未使用且堆在pq [1]到pq [n]中。我们只通过函数less() 和exch()来访问元素。
堆有序化
打破堆的状态,然后再遍历堆并按照要求将堆的状态恢复。
由下至上的堆序列化(上浮)
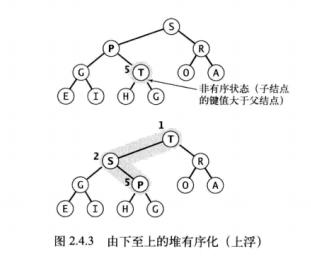
private void swim(int n) {
// 第一层 父节点小于子节点
while (n > 1 && less(n / 2, n)) {
exch(n / 2, 2);
//n=父节点
n = n / 2;
}
}
由上至下的堆序列化(下沉)
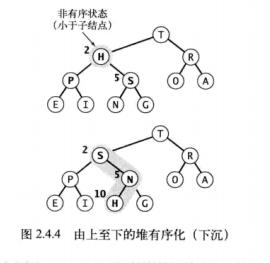
private void sink(int k){
//子节点小于等于最后一个
while(2 * k <= N){
int j = 2 * k;
if(j <N && less(j,j + 1))j ++;//如果第二个子节点大,就取大的
if(!less(k,j))break;//跟父节点比对,父节点大就break;
exch(k,j);//交换后 k = j 继续下沉
k = j;
}
}
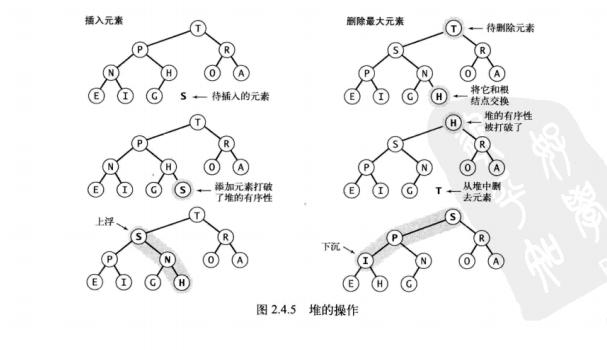
插入元素时,将新元素加到数组末尾,增加堆的大小并让这个新元素上浮到合适的位置。
删除最大元素时,从数组顶端删去最大的元素并将数组的最后一个元素放到顶端,减小堆的大小并让这个元素下沉到合适的位置。
api&实现

public class MaxPQ<T extends Comparable<T>> {
private boolean less(int i, int j) {
return pq[i].compareTo(pq[j]) < 0;
}
private void exch(int i, int j) {
T t = pq[i];
pq[i] = pq[j];
pq[j] = t;
}
private T[] pq;
private int N = 0; //存放到[1-N]中 0没使用
public MaxPQ(int maxN) {
pq = (T[]) new Comparable[maxN + 1];
}
public boolean isEmpty() {
return N == 0;
}
public int size() {
return N;
}
public T delMax() {
T max = pq[1];
exch(1, N--);
pq[N + 1] = null;//防止对象游离态
//下沉
sink(1);
return max;
}
private void sink(int i) {
while (2 * i <= N) {
int j = 2 * i;
if (j < N && less(j, j + 1)) {
j++;
}
if (!less(i, j)) {
break;
}
exch(i, j);
i = j;
}
}
public void insert(T n) {
pq[++N] = n;
//上浮
swim(N);
}
private void swim(int n) {
while (n > 1 && less(n / 2, n)) {
exch(n / 2, 2);
n = n / 2;
}
}
}
特点
在某些数据处理的场合,总数据量太大(可以认为输入是无限的),
无法排序(甚至无法全部装进内存)。如果将每个新的输入和已知的 M 个最大(或最小)元素比较,除非 M 较小,
否则这种比较的代价会非常高昂。如果有了优先队列,就只用一个能存储 M 个元素的队列即可。
利用在数组中无需指针即可沿树上下移动的便利。
堆排序
为了方便书写根节点从0开始
public static void sort(Comparable[] a) {
int N = a.length - 1;//一共有N个 元素
/**
* 初始化堆
*/
for (int i = (N - 1) / 2; i >= 0; i--) {
sink(a, i, N);
}
/**
* 现在堆有序状态
*/
while (N >= 0) {
exch(a, 0, N--);
sink(a, 0, N);
}
}
public static void sink(Comparable[] a, int k, int n) {
while (2 * k + 1 <= n) {
int j = 2 * k + 1;
if (j < n && less(a, j, j + 1)) {
j++;
}
if (!less(a, k, j)) {
break;
}
exch(a, j, k);
k = j;
}
}
public static boolean less(Comparable[] a, int j, int i) {
return a[j].compareTo(a[i]) < 0;
}
这里我们将堆中的最大元素删除,然后放入堆缩小后数组中空出的位置。
这个过程和选择排序有些类似(按照降序而非升序取出所有的元素),但所需的比较要少很多,因为堆提供了一种从未排序部分找到最大元素的有效方法。


