前缀和：CodeForces 932B Recursive Queries

Description

Let us define two functions f and g on positive integer numbers.

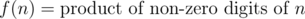
You need to process Q queries. In each query, you will be given three integers l, r and k. You need to print the number of integers xbetween l and r inclusive, such that g(x) = k.

Input

The first line of the input contains an integer Q (1 ≤ Q ≤ 2 × 105) representing the number of queries.

Q lines follow, each of which contains 3 integers l, r and k (1 ≤ l ≤ r ≤ 106, 1 ≤ k ≤ 9).

Output

For each query, print a single line containing the answer for that query.

Examples

input
4
22 73 9
45 64 6
47 55 7
2 62 4
output
1
4
0
8
input
4
82 94 6
56 67 4
28 59 9
39 74 4
output
3
1
1
5

Note

In the first example:

• g(33) = 9 as g(33) = g(3 × 3) = g(9) = 9
• g(47) = g(48) = g(60) = g(61) = 6
• There are no such integers between 47 and 55.
• g(4) = g(14) = g(22) = g(27) = g(39) = g(40) = g(41) = g(58) = 4

题意：

给定一个表达式，根据表达式求值。先输入q，代表有q次询问，接下来q行，分别为l,r,k。表示从l到r有多少个值为k的数字，输出一个整数

思路：

看数据量，q和l,r都很大，所以如果直接暴力会超时。所以要先求出每个数的值是多少。这里通过递归或者循环都能求出来，本人不习惯递归，使用循环求出。然后用二维数组，直接求出从1-i有多少个符合条件的数，二位数组的i代表从1到i有多少符合条件的，j代表的是结果，也就是k。所以求l到r之间等于k的就是ans[r][k] - ans[l-1][k]。具体看代码。

代码：

#include <bits/stdc++.h>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <string>
#include <queue>
#include <stack>
#include <map>
#include <set>

#define IO ios::sync_with_stdio(false);\
    cin.tie(0);\
    cout.tie(0);

typedef long long LL;
const long long INF = 0x3f3f3f3f;
const long long mod = 1e9+7;
const double PI = acos(-1.0);
const int maxn = 1100000;
const char week[7][10]= {"Monday","Tuesday","Wednesday","Thursday","Friday","Saturday","Sunday"};
const char month[12][10]= {"Janurary","February","March","April","May","June","July",
                           "August","September","October","November","December"
                          };
const int daym[2][13] = {{0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31},
    {0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31}
};
const int dir4[4][2] = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};
const int dir8[8][2] = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}, {1, 1}, {-1, -1}, {1, -1}, {-1, 1}};

using namespace std;
using namespace std;

int n, k, ans[maxn][9], q, l, r;

int a[maxn];
void init()//将1-maxn的值求出来
{
    for(int i=1; i<=maxn; i++)
    {
        int sum=1;
        int ii=i;
        while(ii)
        {
            if(ii%10!=0)
                sum=sum*(ii%10);
            ii/=10;
        }
        int sum1=1;
        while(1)
        {
            if(sum<10)
            {
                a[i]=sum;
                break;
            }
            while(sum)
            {
                if(sum%10!=0)
                    sum1=sum1*(sum%10);
                sum/=10;
            }
            sum=sum1;
            sum1=1;
        }

    }
}

int main()
{
    init();
    for (int i = 1; i <= maxn; i++)//将每个数的结果加上
    {
        ans[i][a[i]]++;
    }
    for (int i = 1; i <= 9; i++)
        for (int j = 2; j <= maxn; j++)//将从1到j的等于i的数求出来。
            ans[j][i] += ans[j-1][i];
    cin >> q;
    while (q--)
    {
        cin >> l>> r>> k;
        cout <<ans[r][k] - ans[l-1][k]<<endl;
    }
}