《深入理解计算机系统(第三版)》第二章学习总结
第二章:信息的表示和处理
1.二进制与十六进制:
①十六进制数字:0 – F,例子:25A4B
② 二进制数字:0 – 1,例子:0001 0111 0011 1010 0100 1100
③相互转换:十进制→ 十六进制:Mod(10,16)(倒序排列)
2.字和数据大小:
① 字长决定了系统虚拟地址空间的最大大小,对于典型32位机器而言,虚拟地址范围为0 - 232-1,程序最多访问232,所以32位机器支持最大内存为4G。
②一般数据类型的字节数,重点为指针类型的字节数为全字长。
3.寻址和字节顺序:
分为大端法和小端法,IBM和Sun的个人计算机通常使用大端法。
4.布尔代数与位级运算:
①基本位运算符:|(逻辑或),&(逻辑与),~(逻辑非),^(逻辑异或)
②重要结论:a^a = 0(通过异或交换两个变量的值)
5.移位运算及其重要结论:
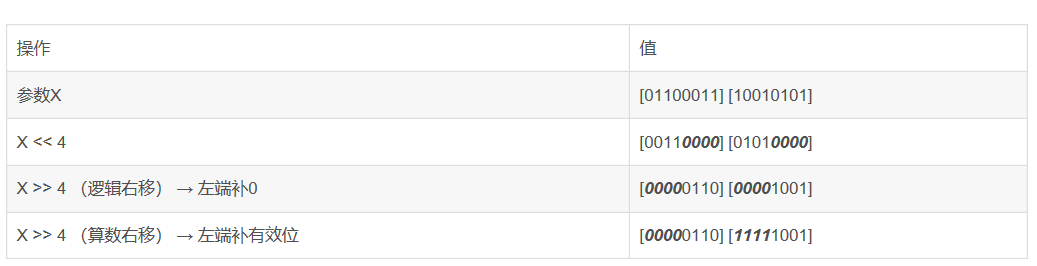
6.整数的表示:
①无符号数的编码.
②补码的编码.
③有符号数与无符号数之间的转换.
④截断数字.
7.整数运算:
①无符号数的加法:
重要结论:模数加法形成了阿贝尔群,可交换结合,每个元素都有一个加法逆元。
②补码加法;
③补码的非;
④无符号乘法;
⑤补码乘法:
重要结论:设为二进制表示的无符号整数,对于任意k0,有以下公式:
即:一个二进制表示数乘以,相当于在位模式右边补了k个0(不溢出的情况),相当于一种移位操作,C表达式中x << k等价于 x * pwr2k,许多C语言编译器视图以移位,加法和减法的组合来消除很多整数乘以常数的情况。
例如:x*14,利用等式14=,编译器将乘法重写为(x<<3)+(x<<2)+(x<<1),实现将一个乘法替换为三个移位运算和三个加法,减少时钟周期提高运算效率。
⑥补码除法:
向零舍入:即乘法的逆运算,执行算数右移k位即除以,因为移位导致结果向下舍入,根据向零舍入的要求,通过偏置, = 可以得到正确的舍入结果。
8. 浮点数的IEEE表示:
① IEEE浮点表示:
- 符号:s通过其值1负和0正决定V的正负,对于V=0另作解释。
- 尾数:M是一个二进制小数,它的范围是1 – 2-ε,或者0 – 1-ε
- 阶码:E的作用是对浮点数加权,权重是2的E次幂(可能是负数)
②通过将浮点数的位划分为3个字段,分别进行编码,类似科学计数法:
- 1个单独的符号位s,直接编码符号s
- k位的阶码字段,exp=ek-1···e0,编码解码E
- n位的小数字段,frac=fn-1···f0,编码尾数M,但是该值依赖于E是否为0
③ 浮点表示的三种情况:
- 规格化的值:
普遍情况,当exp不全为0,也不全为1,此情况解码以偏置形式表示有符号整数,即E = e – Bias,e是无符号数,e表示为阶码位的编码ek-1···e0,而Bias是一个等于(单精度k=8,双精度k=11)的偏置值,由此产生指数的取值范围即:(单精度-126~+127,双精度-1022~+1023),对于frac解释为描述小数值f,期中0≤f<1,其二进制表示为0.fn-1···f0,当尾数定义为M
= 1+f时,叫做隐含以1开头的表示,所以M = 1.fn-1···f0,因为二进制的基数是2,且我们总能在不溢出的范围内调整阶码,使得尾数M的范围总在1≤M<2中,符合IEEE定义M的范围,从而表示小数。 - 非规格化的值:
当阶码exp域全0,阶码值为E = 1-Bias,而尾数值为M = f,不包含隐含开头都 1(为什么),非规格化的值用来表示0和非常接近0的小数,因为规格化要求M≥1,所以无法表示0,实际上+0.0的浮点表示位模式全0,而当符号位为1时候得到-0.0,逐渐溢出的属性使得数值均匀的接近0.0(?) - 特殊值:
当阶码exp域全1,当frac全0表示无穷,根据符号位的表示的正负来确定正负无穷,无穷能表示溢出的结果,当小数域非零时,NaN被称为不是一个数的缩写,一些运算结果为虚数,无法表示。
9.浮点表示的整数与补码表示整数之间的关系:
以十进制数12345为例,其补码二进制表示为[00000000000000000000001100000011 1001],用IEEE浮点型表示,将小数点左移13位,得到12345 = 1.10000001110012,丢弃开头1,由于32位s=1,k=8,n=23,所以在末尾追加10个0,得到[10000001110010000000000],即frac字段,因为E = e – Bias,即e = 13 + 127,得其阶码二进制表示为10001100,加上符号为0,得到单精度12345二进制表示为[01000110010000001110010000000000],与[000000000000000000000011000000111001]在红线处相同,这说明相关区域对应整数低位,恰好在等于1的最高位之前相同,因为此标准略去开头位1,其余部位都是相配的。
10.舍入规则:
向偶数舍入:使得最低有效位为偶数的舍入方法,来确定浮点数的近似值(IEEE默认)。
11.浮点运算:
1.IEEE定义简单规则:把浮点值x,y看成实数,某个运算⊙定义在实数上,算数计算产生Round(x⊙y),其结果对精确结果进行了舍入。
2.浮点运算因为精度受限不满足结合律,例如:(3.14+e10)-e10=0.0,3.14+(e10-e10)=3.14,这是浮点运算构成代数系统最缺少的群属性。
3.浮点数满足单调性属性,如果有a≥b,则有x + a≥x + b(?)
4.C语言虽然有float和double类型,但是未明确要求机器满足IEEE标准。
总结:
精读第二章之后,我们更加深刻地理解了什么叫做信息=位+上下文,可以这样说:系统中所有的信息——包括磁盘文件、存储器中的程序、存储器中存放的用户数据以及网络上传送的数据,都是一串比特表示的。区分不同数据对象的唯一方法是我们读到这些数据对象时的上下文。比如,在不同的上下文中,同样的字节序列可能表示一个整数、浮点数、字符串或者及其指令。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号