JSI-GAN: GAN-Based Joint Super-Resolution and Inverse Tone-Mapping with Pixel-Wise Task-Specific
1. 摘要
使用分治策略来处理SR-iTM问题;将其分成三个任务相关的子网络:图像重建子网络(image reconstruction subnet),细节恢复子网络 (detail restoration subnet),局部对比度增强子网络(local contrast enhancement subnet),从而学习到一组像素级的逐像素的1维可分离卷积用于复原细节,像素级的2维局部卷积核来用于对比度增强。此外,作者提出一种可增强细节信息的GAN loss,可同时增强细节恢复和对比度复原。
2. 介绍
一方面,作者认为SR-ITM这个问题需要同时考虑两个问题:如何在上采样的结果中恢复细节;由于比特位数增加如何增强局部的对比度信息(enhance local contrast)
GAN网络可用于生成图片,但作者认为GAN网络会导致主观的图像质量提高的同时降低客观的评价指标(PSNR,SSIM),直接使用传统的GAN网络的结构会导致缺少相应的细节和局部的对比度,因此本文中使用了新的detail loss,使得生成的图片与GT的细节更相符合,并且使用一种feature-matching loss,用来减轻在训练过程中客观评价的drop。
本文主要有以下几个贡献:
- 首先提出了一个用于联合SR-ITM的GAN框架,称为JSI-GAN,具有新颖的细节损失和特征匹配损失,可以恢复现实的细节并进行稳定的训练。”
- JSI-GAN的设计旨在具有特定于任务的子网(DR / IR /
LCE子网络),这些子网具有像素级的1D可分离滤波器以改善局部细节,并具有2D局部滤波器以增强局部对比度,方法是考虑给定放大系数的局部上采样操作。 - DR子网专注于高频分量,以精心还原HR HDR输出的细节,而LCE子网通过专注于LRSDR输入的基础层分量,有效地恢复了局部对比度。
3. 网络结构
3.1 生成器

3.1.1 细节恢复子网络(detail restoration subnet)
是上采样滤波器, 输入是细节层 $\large X_d$ 包含了 LR SDR 输入图片的高频分量, $\large X_d = X \oslash X_b$ , 其中$\large X_b$是X应用引导滤波器的输出, $\large \oslash$表示按元素相除. 在我们的实现中,向分母添加一个较小的值$\large 10^{-15}$,以防止在$\large X_b$接近零的情况下$\large X_d$发散.$\large X_d$用于生成水平和垂直一维可分离滤波器.
残差模块(Res-Block) RB定义:
$\large RB(x) = (Conv \circ RL \circ Cove \circ RL)(x) +x$, 其中 x 是 ResBlock 的输入, Conv 是卷积层, RL是 ReLU激活函数.
水平1D滤波器 $\large f_{1D}^h = (Conv \circ RL \circ RB^4 \circ Conv)(X_d)$, 其中$\large RB^n$表示 n个 ResBlock 串行级联. 垂直 1D滤波器$\large f_{1D}^v$用同样的方式获得. 在生成1D水平和垂直滤波器时,除最后一个卷积层外的所有层都共享.
最后两个卷积层中的每一个都由41×scale×scale 输出通道组成,其中41是一维可分离kernel的长度,每个通道应用于其对应的网格位置,scale × scale 考虑了对于上采用因子scale 的像素混洗重组操作. 动态可分离上采样操作 ($\large \dot{*}_s$) 表示使用两个1D可分离滤波器产生空间上采样输出.
DR subnet 输出为: $\large D = X_d \quad \dot{*}s \quad (f^v, f^h_{1D})$
生成的一维kernel是位置特定的,也是细节特定的,因为针对不同的细节层生成了不同的kernel,这与训练后固定的卷积滤波器不同, 在实现中, 首先通过每个比例通道的局部过滤将$\large f^v_{1D}$应用于细节层, 然后在其输出应用$\large f^h_{1D}$, 最后,将像素混洗应用到具有scale * scale 个通道的最终滤波输出上,以进行空间放大。
3.1.2 局部对比度增强网络(Local Contrast Enhancement(LCE) Subnet)
LCE子网在每个像素网格位置生成一个9×9 2D局部滤波器, 同样是上采样滤波器, 在最后一层具有9×9×scale×scale输出通道
$\large f_{2D} = (Conv \circ RL \circ RB^4 \circ Conv)(X_b)$
LCE 网络输出$\large C_l = 2 \times sigmoid(X_b \dot{ \ast} f_{2D})$
由于将Cl视为LCE掩码,并且将其逐个元素地与IR和DR子网的两个输出之和相乘,因此JSInet与singmoid函数更好的融合,没有它,初始预测输出(与Cl相乘后)的像素值太小,需要更长的训练时间才能使JSInet的最终HR HDR输出达到合适的像素范围。
3.1.3 图像重建网络Image Reconstruction (IR)Subnet
输入LR SDR 图像X, 产生中间特征 $\large i_{IR} = (RB \circ Conv)(X)$
IR 网络的输出 $\large I= (Conv \circ PS \circ RL \circ Conv \circ RL \circ RB^3)([i_{IR}, i_{DR}])$, PS 是 pixel-shuffle 操作, [x, y] 表示在通道方向x与y 进行拼接.
最终HR HDR预测值$\large P = (I+ D) \times C_l$
3.2 判别器

输入x (P[生成器预测的结果] 或 Y[ground truth]), 判别器的输出 $\large D^f (x) = (BN \circ FC1 \circ BN \circ FC512 \circ LRL \circ BN \circ 4Conv2 \circ DB^4 \circ LRL \circ 3Conv1)(x)$
其中, BN表示 batch normalization, LRL 表示 Leaky ReLU激活slope size 为0.2, FCk 表示全连接层有k个输出通道. K Conv s表示k*k 大小的 kernel size , stride 为s
DB(DisBlock) $\large DB(x) = (LRL \circ BN \circ 3Conv1 \circ LRL \circ BN \circ 4Conv2)(x)$
对抗损失(Adversarial loss):
$\large L^D_{adv} = \underset{Y}{\mathbb{E}}[ max(0, \widetilde{Q}{Y,P}^{(-)} ] + \underset{P}{\mathbb{E}}[ max(0, \widetilde{Q}^{(+)}) ]$
$\large L^G_{adv} = \underset{P}{\mathbb{E}}[max(0, \widetilde{Q}^{(-)}{P,Y})] + \underset{Y}{\mathbb{E}}[ max(0, \widetilde{Q}^{(+)}) ]$
其中, $\large \widetilde{Q}^{(\pm )}{P,Y} = 1 \pm \widetilde{D}$, $\quad \widetilde{D}_{P,Y} = D_f(P) - \mathbb{E}_YD_f(Y)$
feature-matching loss:
$\large L_{fm} = \sum^4_{i=1}|| fm_i(Y) - fm_i(P) ||_2$
Detail GAN loss: $\large L_{adv}^d$为了增强训练稳定性和提供局部对比度和细节产生更好的结果.
d 上标表示 细节层. 对于$\large L_{adv}^d$ 我们采用不同于第一鉴别器(D1)的第二鉴别器(D2),两者的结构相同,但D2取两个输入Pd和Yd,由等式(1)计算得出$[\large P_d = P \oslash P_b]$。
total loss:
$\large L_{D_1} = L_{adv}^{D_1}, \quad L_{D_2} = \lambda_d \cdot L_{adv}^{d, D_2}$
$\large L_G = \lambda_{rec} \cdot || Y-P ||2 + \lambda \cdot (L_{adv}^G + \lambda_d \cdot L_{adv}^{d,G}) + \lambda_{fm} \cdot (L_{fm} + \lambda_d \cdot L_{fm}^d)$
上标d表示细节层成分(Pd,Yd)的损失
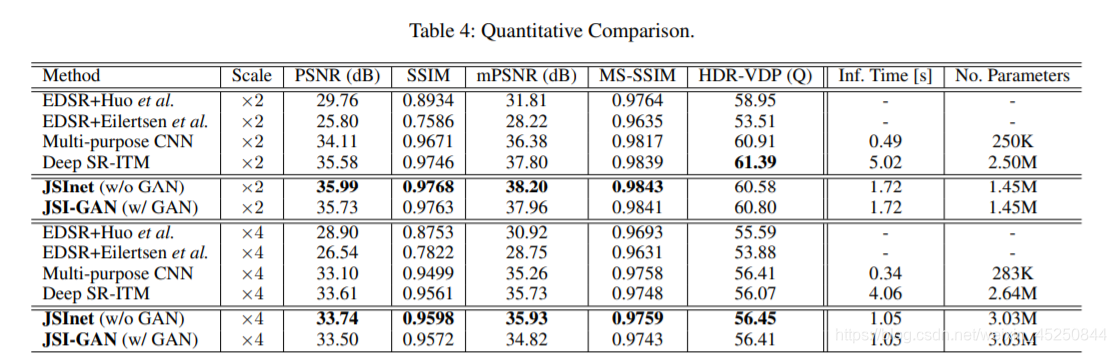
4. 实验