12、线性判别分析（linear discriminant analysis，LDA）——降维

1、 线性判别分析（linear discriminant analysis，LDA）

​线性判别分析（Linear Discriminant Analysis，LDA）是一种经典的降维方法。和主成分分析PCA不考虑样本类别输出的无监督降维技术不同，LDA是一种监督学习的降维技术，数据集的每个样本有类别输出。

LDA分类思想简单总结如下：

1). 多维空间中，数据处理分类问题较为复杂，LDA算法将多维空间中的数据投影到一条直线上，将d维数据转化成1维数据进行处理。

2). 对于训练数据，设法将多维数据投影到一条直线上，同类数据的投影点尽可能接近，异类数据点尽可能远离。

3). 对数据进行分类时，将其投影到同样的这条直线上，再根据投影点的位置来确定样本的类别。

如果用一句话概括LDA思想，即“投影后类内方差最小，类间方差最大”。

2、图解LDA核心思想

​假设有红、蓝两类数据，这些数据特征均为二维，如下图所示。我们的目标是将这些数据投影到一维，让每一类相近的数据的投影点尽可能接近，不同类别数据尽可能远，即图中红色和蓝色数据中心之间的距离尽可能大。

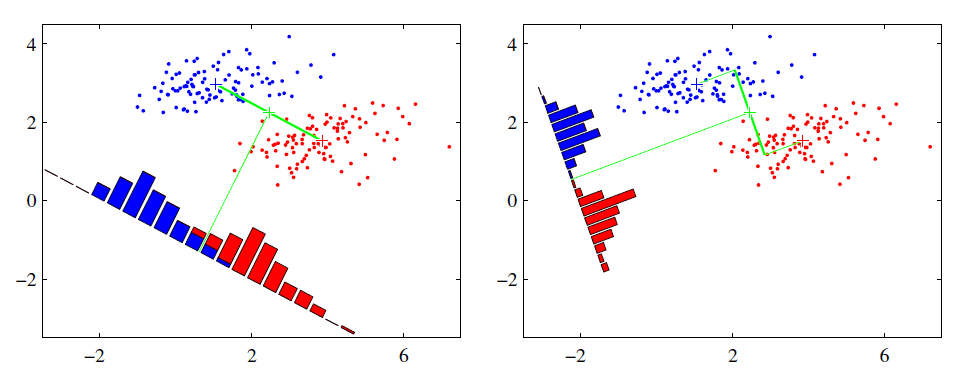
左图和右图是两种不同的投影方式。

​左图思路：让不同类别的平均点距离最远的投影方式。

​右图思路：让同类别的数据挨得最近的投影方式。

​从上图直观看出，右图红色数据和蓝色数据在各自的区域来说相对集中，根据数据分布直方图也可看出，所以右图的投影效果好于左图，左图中间直方图部分有明显交集。

​以上例子是基于数据是二维的，分类后的投影是一条直线。如果原始数据是多维的，则投影后的分类面是一低维的超平面。

3、二类LDA算法原理

​输入：数据集 $D={(\boldsymbol x_1,\boldsymbol y_1),(\boldsymbol x_2,\boldsymbol y_2),...,(\boldsymbol x_m,\boldsymbol y_m)}​$，其中样本 $\boldsymbol x_i ​$ 是n维向量，$\boldsymbol y_i \epsilon {(0, 1)}​$，降维后的目标维度 $d​$。定义

​$N_j(j=0,1)$ 为第 $j$ 类样本个数；

​$X_j(j=0,1)$ 为第 $j$ 类样本的集合；

​$u_j(j=0,1)​$ 为第 $j​$ 类样本的均值向量；

​$\sum_j(j=0,1)$ 为第 $j$ 类样本的协方差矩阵。

​其中

$ u_j = \frac{1}{N_j} \sum\nolimits_{x \in {X_j}} x \left( {j = 0{\rm{,}}1} \right), \sum_j = \sum\nolimits_{x \in {X_j}} (\boldsymbol x-u_j)(\boldsymbol x-u_j)^T(j=0,1) $ ​

假设投影直线是向量 $\boldsymbol w$，对任意样本 $\boldsymbol x_i$，它在直线 $w$上的投影为 $\boldsymbol w^Tx_i$，两个类别的中心点 $u_0$, $u_1 $在直线 $w$ 的投影分别为 $\boldsymbol w^Tu_0$ 、$\boldsymbol w^Tu_1$。

​LDA的目标是让两类别的数据中心间的距离 $\| \boldsymbol w^Tu_0 - \boldsymbol w^Tu_1 \|_2^2$ 尽量大，与此同时，希望同类样本投影点的协方差$\boldsymbol w^T \sum_0 \boldsymbol w$、$\boldsymbol w^T \sum_1 \boldsymbol w$ 尽量小，最小化 $\boldsymbol w^T \sum_0 \boldsymbol w - \boldsymbol w^T \sum_1 \boldsymbol w​$ 。定义类内散度矩阵

$ S_w = \sum_0 + \sum_1 = \sum{\boldsymbol x\epsilon X_0}(\boldsymbol x-u0_)(\boldsymbol x-u_0)^T + \sum{\boldsymbol x\epsilon X_1}(\boldsymbol x-u_1)(\boldsymbol x-u_1)^T $ ​

类间散度矩阵 $S_b = (u_0 - u_1)(u_0 - u_1)^T$

​ 据上分析，优化目标为

$ \mathop{\arg\max}\boldsymbol w J(\boldsymbol w) = \frac{\| \boldsymbol w^Tu_0 - \boldsymbol w^Tu_1 \|_2^2}{\boldsymbol w^T \sum_0\boldsymbol w + \boldsymbol w^T \sum_1\boldsymbol w} = \frac{\boldsymbol w^T(u_0-u_1)(u_0-u_1)^T\boldsymbol w}{\boldsymbol w^T(\sum_0 + \sum_1)\boldsymbol w} = \frac{\boldsymbol w^TS_b\boldsymbol w}{\boldsymbol w^TS_w\boldsymbol w} $

根据广义瑞利商的性质，矩阵 $S_{w}^{-1} S_b$ 的最大特征值为 $J(\boldsymbol w)$ 的最大值，矩阵 $S_{w}^{-1}S_b$ 的最大特征值对应的特征向量即为 $\boldsymbol w$。

4、LDA算法流程总结

LDA算法降维流程如下：

​输入：数据集 $D = { (x_1,y_1),(x_2,y_2), ... ,(x_m,y_m) }$，其中样本 $x_i $ 是n维向量，$y_i \epsilon {C_1, C_2, ..., C_k}$，降维后的目标维度 $d$ 。

​输出：降维后的数据集 $\overline{D} $ 。

步骤： 1). 计算类内散度矩阵 $S_w$。 2). 计算类间散度矩阵 $S_b​$ 。 3). 计算矩阵 $S_{w}^{-1}S_b​$ 。 4). 计算矩阵 $S_{w}^{-1}S_b$ 的最大的 d 个特征值。 5). 计算 d 个特征值对应的 d 个特征向量，记投影矩阵为 W 。 6). 转化样本集的每个样本，得到新样本 $P_i = W^Tx_i​$ 。 7). 输出新样本集 $\overline{D} = { (p_1,y_1),(p_2,y_2),...,(p_m,y_m) }​$

5、LDA和PCA区别

相同点:

1). 两者均可以对数据进行降维； 2). 两者在降维时均使用了矩阵特征分解的思想； 3). 两者都假设数据符合高斯分布；

不同点:

LDA: 有监督的降维方法； 降维最多降到 k-1；可以用于降维；还可以用于分类； 选择分类性能最好的投影方向；更明确，更能反映样本间差异；

PCA: 无监督的降维方法；维降维多少没有限制；只用于降维；选择样本点投影具有最大方差的方向；目的较为模糊。

6、LDA优缺点

优点：1). 可以使用类别的先验知识； 2). 以标签、类别衡量差异性的有监督降维方式，相对于PCA的模糊性，其目的更明确，更能反映样本间的差异；

缺点：1). LDA不适合对非高斯分布样本进行降维； 2). LDA降维最多降到分类数k-1维； 3). LDA在样本分类信息依赖方差而不是均值时，降维效果不好； 4). LDA可能过度拟合数据。