8、随机森林（Random Forest，RF）算法——监督、分类/回归

1、随机森林（Random Forest，RF）算法

随机森林（Random Forest，RF）算法由Leo Breiman和Adele Cutler提出，可以用来解决分类或回归等问题。

基本单元：决策树

思想：集成学习（Bagging）

优点：具有极好的准确率；能够有效地运行在大数据集上；能够处理具有高维特征的输入样本，而且不需要降维；能够评估各个特征在分类问题上的重要性；抗过拟合能力比较强；对于缺省值问题也能够获得很好得结果。

缺点：对于小数据或者低维数据（特征较少的数据），可能难以产生较好的分类；在解决回归问题时，并没有在分类中表现的那么好。

2、集成学习（Ensemble Learniing）之Bagging算法

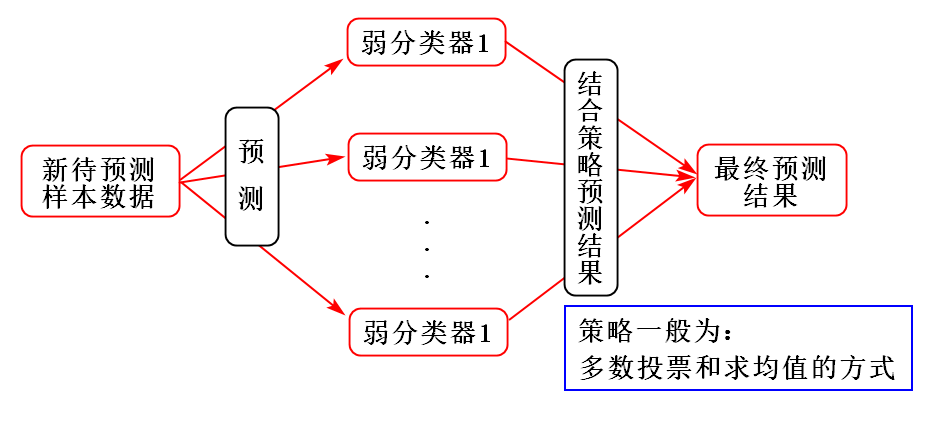
Bagging算法通过对训练样本有放回地抽取，由此产生多个训练数据的子集，并在每一个训练集的子集上训练一个分类器，最终分类结果是由多个分类器的分类结果投票而产生的。对于 Bagging 思想集成的随机森林，是可以并行训练的，正是因为每个弱分类器之间不相互影响。

Bagging算法训练出来的模型在预测新样本分类的时候，会使用多数投票或者求均值的方式来统计最终的分类结果。

Bagging算法的弱学习器可以是基本的算法模型，比如：Linear、Ridge、Lasso、Logistic、Softmax、ID3、C4.5、CART、SVM、KNN等。

Bagging常用模型：随机森林(RF)。

其示意图如下：

   

3、随机森林算法基本原理

随机森林算法是一种重要的基于Bagging的集成学习方法，通过对数据集的自助法（Bootstrap）重采样生成多个不同的数据集，并在每一个数据集上训练一棵分类树，最终结合每一棵分类树的预测结果作为随机森林的预测结果。即”三个臭皮匠顶个诸葛亮”。因此，集成学习方法的泛化能力比单个学习算法的泛化能力强很多。

随机算法流程

随机森林算法是通过训练多个决策树，生成模型，然后综合利用多个决策树进行分类。随机森林算法只需要两个参数：构建的决策树个数${n_{tree}}$，在决策树的每个结点进行分裂时需要考虑的输入特征的个数$k$，通过$k$可以取为${\rm{lo}}{{\rm{g}}_2}n$，其中$n$表示的是原数据集中特征的个数。对于单棵决策树的构建，可以分为如下的步骤：

• 假设训练样本的个数为m，则对于每一棵决策树的输入样本的个数都为$m$，且这$m$个样本是通过从训练集中有放回地随机抽取得到的。
• 假设训练样本特征的个数为$n$，对于每一棵决策树的样本特征是从该$n$个特征中随机挑选$k$个，然后从这$k$个输入特征里选取一个最好的进行分裂。
• 每棵树都一直这样分裂下去，直到该结点的所有训练样例都属于同一类。在决策树分裂过程中不需要剪枝。

4、随机森林算法Python实践

1）CART决策树

2）训练

3）测试

参考文献 

[1] 赵志勇. Python机器学习算法[M]. 北京：电子工业出版社，2017.

[2] 李航. 统计学习方法[M]. 北京：清华大学出版社，2012.

[3] Peter. 机器学习实战[M]. 北京：人民邮电出版社，2013.

[4] 周志华. 机器学习[M]. 北京：清华大学出版社，2016.

附录

数据集下载：

链接：https://pan.baidu.com/s/1oPYOcTHCbuQ9YAAAxIhL-Q 
提取码：662x