1、逻辑回归(Logistic Regression)算法 —— 监督、分类
1、逻辑回归(Logistic Regression)模型
Logistic回归模型,是一种广义的线性回归分析模型,常用于数据挖掘,疾病自动诊断,经济预测等领域。
适用条件:主要面向二分类线性可分问题。
2、系统模型
(1)超平面
对于如图线性可分的问题,需要找到一条直线,能够将两个不同的类区分开,这条直线称为超平面。
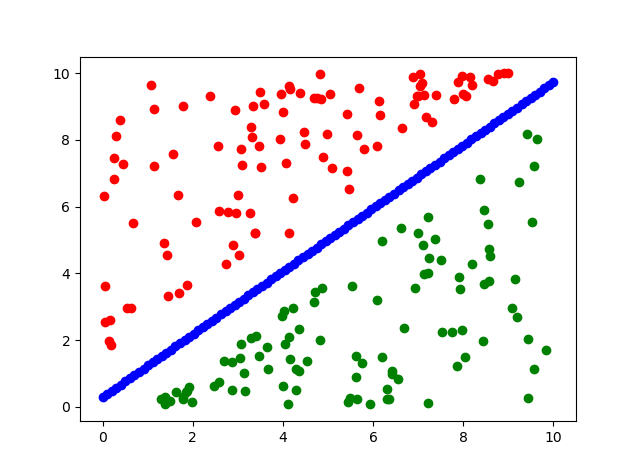
对于上述超平面,可表示如下:
$Wx + b = 0$
其中$W$为权重,$b$为偏置。在Logistic回归模型中,通过对训练样本的学习,可得到超参数$W$和$b$,最终得到该超平面。
(2)类别映射
令$y = \sigma \left( {Wx + b} \right) = \sigma \left( {\sum\limits_{j = 1}^n {{W_j}} {x_j} + b} \right)$,$y$取值正负两个类别,可通过Sigmoid函数将样本映射到不同类别中。
对于上式,令${x_0} = 1$,则上式可表示为:
$y = \sigma \left( {\sum\limits_{j = 0}^n {{W_j}} {x_j}} \right)$
Sigmoid函数定义如下:
$\sigma \left( x \right) = \frac{1}{{1 + {e^{ - x}}}}$
函数图像如下: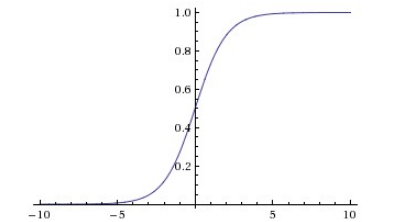
- 由函数图像可知,Sigmoid函数是单调增函数,输出范围在[0,1]之间,且越是负向增大,越接近于0,逼近速度越来越慢;越是正向增大,越接近于1,逼近速度也是越来越慢;因为 Sigmoid函数求导比较容易,可解释性也很强,所以在历史上被广泛的使用。与此同时,Sigmoid函数也有两个很大的缺点:首先是Sigmoid函数会造成梯度消失问题,从图像中我们也可以得知,当输入特别大或是特别小时,神经元的梯度几乎接近于0,这就导致神经网络不收敛,模型的参数不会更新,训练过程将变得非常困难。
其导函数$\sigma {\rm{'}}\left( x \right)$为:
$\sigma {\rm{'}}\left( x \right) = \frac{{{e^{ - x}}}}{{{{\left( {1 + {e^{ - x}}} \right)}^2}}} = \sigma \left( x \right)\left[ {1 - \sigma \left( x \right)} \right]$
(3)构造损失函数 (极大似然法,交叉熵损失函数)
1)步骤一
对于输入向量$X$,其属于正类的概率为:
$P\left( {y = 1|X{\rm{,}}W{\rm{,}}b} \right) = \sigma \left( {WX + b} \right) = \frac{1}{{1 + {e^{ - \left( {WX + b} \right)}}}}$
其属于负类的概率为:
$P\left( {y = 0|X{\rm{,}}W{\rm{,}}b} \right) = 1 - P\left( {y = 1|X{\rm{,}}W{\rm{,}}b} \right) = 1 - \sigma \left( {WX + b} \right) = \frac{{{e^{ - \left( {WX + b} \right)}}}}{{1 + {e^{ - \left( {WX + b} \right)}}}}$
统一形式:
对于输入向量$X$,其属于$y \in \{ 0{\rm{,}}1\}$类的概率为:
$P\left( {y|X{\rm{,}}W{\rm{,}}b} \right) = {\left( {\sigma \left( {WX + b} \right)} \right)^y}{\left( {1 - \sigma \left( {WX + b} \right)} \right)^{1 - y}}$
2)步骤二
要求上述问题中的超参数$W$和$b$,可以使用极大似然法对其进行估计。
假设训练数据集有$m$个训练样本$\{ \left( {{X^{\left( 1 \right)}}{\rm{,}}{y^{\left( 1 \right)}}} \right){\rm{,}}\left( {{X^{\left( 2 \right)}}{\rm{,}}{y^{\left( 2 \right)}}} \right){\rm{,}} \cdots {\rm{,}}\left( {{X^{\left( m \right)}}{\rm{,}}{y^{\left( m \right)}}} \right)\} $,则其似然函数为:
${L_{W{\rm{,}}b}} = \prod\limits_{i = 1}^m {\left[ {{{\left( {\sigma \left( {W{X^{\left( i \right)}} + b} \right)} \right)}^{{y^{\left( i \right)}}}}{{\left( {1 - \sigma \left( {W{X^{\left( i \right)}} + b} \right)} \right)}^{1 - {y^{\left( i \right)}}}}} \right]} $
进一步,对上式取对数得交叉熵损失函数:
${l_{W{\rm{,}}b}} = - \frac{1}{m}{\rm{ln}}{L_{W{\rm{,}}b}} = - \frac{1}{m}\sum\limits_{i = 1}^m {\left[ {{y^{\left( i \right)}}{\rm{ln}}\left( {\sigma \left( {W{X^{\left( i \right)}} + b} \right)} \right) + \left( {1 - {y^{\left( i \right)}}} \right){\rm{ln}}\left( {1 - \sigma \left( {W{X^{\left( i \right)}} + b} \right)} \right)} \right]} $
其中,$m$为训练样本数。
为此,可以得出如下最小化问题:
$\mathop {{\rm{min}}}\limits_{W{\rm{,}}b} {\rm{ }}{l_{W{\rm{,}}b}}$
为了求解上述最小化问题得超参数$W$和$b$(合并为$W$),可以使用梯度下降法进行求解。
注:最小二乘(Least Squares)、岭回归(Ridge Regression)和Logistic回归(Logistic Regression)的损失函数都是凸优化问题。
3、批量梯度下降法(Batch Gradient Descent,BGD)
根据梯度下降时使用数据量的不同,梯度下降可以分为3类:批量梯度下降(Batch Gradient Descent,BGD)、随机梯度下降(Stochastic Gradient Descent, SGD)和小批量梯度下降(Mini-Batch Gradient Descent, MBGD)。选用批量梯度下降进行最优化问题的求解。
批量梯度下降的详细过程如下:
- 随机选取一个超参数初始点${W_0}$;
- 重复以下过程:
- 确定梯度下降的方向:
${\nabla _{{W_j}}}\left( {{l_{W{\rm{,}}b}}} \right) = \frac{{\partial {l_{W{\rm{,}}b}}}}{{\partial {W_j}}} = - \frac{1}{m}\sum\limits_{i = 1}^m {\left( {{y^{\left( i \right)}} - \left( {\sigma \left( {W{X^{\left( i \right)}} + b} \right)} \right)} \right)} x_j^{\left( i \right)}$
-
- 选择步长$\alpha$
- 更新权值:${W_{j + 1}} = {W_j} + \alpha \cdot {\nabla _{{W_j}}}\left( {{l_{W{\rm{,}}b}}} \right)$
- 直到满足终止条件
证明:
令$\sigma \left( Z \right) = \sigma \left( {W{X^{\left( i \right)}} + b} \right) = \sigma \left( {\sum\limits_{j = 1}^n {{W_j}X_j^{\left( i \right)}} + b} \right)$
且有:$\sigma {\rm{'}}\left( Z \right) = \sigma \left( Z \right)\left( {1 - \sigma \left( Z \right)} \right)$
则可得:
$\begin{array}{l}
\frac{{\partial {l_{W{\rm{,}}b}}}}{{\partial {W_j}}} = - \frac{1}{m}\sum\limits_{i = 1}^m {\left( {\frac{{{y^{\left( i \right)}}}}{{\sigma \left( Z \right)}} - \frac{{\left( {1 - {y^{\left( i \right)}}} \right)}}{{\left( {1 - \sigma \left( Z \right)} \right)}}} \right)} \frac{{\partial \sigma \left( Z \right)}}{{\partial {W_j}}}\\
= - \frac{1}{m}\sum\limits_{i = 1}^m {\left( {\frac{{{y^{\left( i \right)}}}}{{\sigma \left( Z \right)}} - \frac{{\left( {1 - {y^{\left( i \right)}}} \right)}}{{\left( {1 - \sigma \left( Z \right)} \right)}}} \right)} \sigma {\rm{'}}\left( Z \right)x_j^{\left( i \right)}\\
= - \frac{1}{m}\sum\limits_{i = 1}^m {\left( {\frac{{\sigma {\rm{'}}\left( Z \right)x_j^{\left( i \right)}}}{{\sigma \left( Z \right)\left( {1 - \sigma \left( Z \right)} \right)}}\left( {{y^{\left( i \right)}} - \sigma \left( Z \right)} \right)} \right)} \\
= - \frac{1}{m}\sum\limits_{i = 1}^m {\left( {\left( {{y^{\left( i \right)}} - \sigma \left( Z \right)} \right)x_j^{\left( i \right)}} \right)}
\end{array}$
4、Logistic回归模型算法Python实践
针对本数据集(见附录)文件,主要分为两个步骤来训练Logistic回归模型:
1)利用训练样本训练模型

# coding:UTF-8 ''' Date:20160901 @author: zhaozhiyong ''' import numpy as np #导入高级的数值工具模块numpy,命名为np def load_data(file_name): '''导入训练数据 input: file_name(string)训练数据的位置 output: feature_data(mat)特征 label_data(mat)标签 ''' f = open(file_name) # 打开文件 feature_data = [] label_data = [] for line in f.readlines(): ##依次读取每行 feature_tmp = [] lable_tmp = [] lines = line.strip().split("\t") #按制表符对字符串进行切片,去掉每行头尾空白 feature_tmp.append(1) # 偏置项,在列表末尾添加新的对象1 for i in range(len(lines) - 1): feature_tmp.append(float(lines[i])) #取出前n-1个数 lable_tmp.append(float(lines[-1])) #取出最后一个数 feature_data.append(feature_tmp) #append() 方法用于在列表末尾添加新的对象。 label_data.append(lable_tmp) f.close() # 关闭文件 return np.mat(feature_data), np.mat(label_data) #转化为矩阵 def sig(x): '''Sigmoid函数 input: x(mat):feature * w output: sigmoid(x)(mat):Sigmoid值 ''' return 1.0 / (1 + np.exp(-x)) def lr_train_bgd(feature, label, maxCycle, alpha): '''利用梯度下降法训练LR模型 input: feature(mat)特征 label(mat)标签 maxCycle(int)最大迭代次数 alpha(float)学习率 output: w(mat):权重 ''' n = np.shape(feature)[1] # 特征个数,读取矩阵的长度(列数) w = np.mat(np.ones((n, 1))) # 初始化权重 i = 0 while i <= maxCycle: # 在最大迭代次数的范围内 i += 1 # 当前的迭代次数 h = sig(feature * w) # 计算Sigmoid值 err = label - h if i % 100 == 0: print ("\t---------iter=" + str(i) + \ " , train error rate= " + str(error_rate(h, label))) w = w + alpha * feature.T * err # 权重修正, .T为矩阵转置 return w def error_rate(h, label): '''计算当前的损失函数值 input: h(mat):预测值 label(mat):实际值 output: err/m(float):错误率 ''' m = np.shape(h)[0] #读取矩阵的长度(行数) sum_err = 0.0 for i in range(m): ##从0循环至m-1 if h[i, 0] > 0 and (1 - h[i, 0]) > 0: sum_err -= (label[i,0] * np.log(h[i,0]) + \ (1-label[i,0]) * np.log(1-h[i,0])) else: sum_err -= 0 return sum_err / m def save_model(file_name, w): '''保存最终的模型 input: file_name(string):模型保存的文件名 w(mat):LR模型的权重 ''' m = np.shape(w)[0] f_w = open(file_name, "w") w_array = [] for i in range(m): w_array.append(str(w[i, 0])) f_w.write("\t".join(w_array)) f_w.close() if __name__ == "__main__": # 1、导入训练数据 print ("---------- 1.load data ------------") feature, label = load_data("data.txt") # 2、训练LR模型 print ("---------- 2.training ------------") w = lr_train_bgd(feature, label, 1000, 0.01) # 3、保存最终的模型 print ("---------- 3.save model ------------") save_model("weights", w) #保存文件
2)利用已训练好的模型对新样本进行预测

# coding:UTF-8 ''' Date:20160901 @author: zhaozhiyong ''' import numpy as np #导入高级的数值工具模块numpy,命名为np from lr_train import sig def load_weight(w): '''导入LR模型 input: w(string)权重所在的文件位置 output: np.mat(w)(mat)权重的矩阵 ''' f = open(w) w = [] for line in f.readlines(): lines = line.strip().split("\t") w_tmp = [] for x in lines: w_tmp.append(float(x)) w.append(w_tmp) f.close() return np.mat(w) def load_data(file_name, n): '''导入测试数据 input: file_name(string)测试集的位置 n(int)特征的个数 output: np.mat(feature_data)(mat)测试集的特征 ''' f = open(file_name) feature_data = [] for line in f.readlines(): feature_tmp = [] lines = line.strip().split("\t") # print (lines[2]) if len(lines) != n - 1: #“<>”和 != 是等价的; continue feature_tmp.append(1) for x in lines: # print (x) feature_tmp.append(float(x)) feature_data.append(feature_tmp) f.close() return np.mat(feature_data) def predict(data, w): '''对测试数据进行预测 input: data(mat)测试数据的特征 w(mat)模型的参数 output: h(mat)最终的预测结果 ''' h = sig(data * w.T) #sig m = np.shape(h)[0] for i in range(m): if h[i, 0] < 0.5: h[i, 0] = 0.0 else: h[i, 0] = 1.0 return h def save_result(file_name, result): '''保存最终的预测结果 input: file_name(string):预测结果保存的文件名 result(mat):预测的结果 ''' m = np.shape(result)[0] #输出预测结果到文件 tmp = [] for i in range(m): tmp.append(str(result[i, 0])) f_result = open(file_name, "w") f_result.write("\t".join(tmp)) f_result.close() if __name__ == "__main__": # 1、导入LR模型 print ("---------- 1.load model ------------") w = load_weight("weights") n = np.shape(w)[1] # 2、导入测试数据 print ("---------- 2.load data ------------") testData = load_data("test_data", n) # 3、对测试数据进行预测 print ("---------- 3.get prediction ------------") h = predict(testData, w)#进行预测 # 4、保存最终的预测结果 print ("---------- 4.save prediction ------------") save_result("result", h)
3)实验结果作图

# -*- coding: utf-8 -*- """ Created on Wed Jul 11 13:51:19 2018 @author: HY """ import matplotlib.pyplot as plt import numpy as np #导入高级的数值工具模块numpy,命名为np def load_data(file_name): '''导入训练数据 input: file_name(string)训练数据的位置 output: feature_data(mat)特征 label_data(mat)标签 ''' f = open(file_name) # 打开文件 feature_data = [] label_data = [] for line in f.readlines(): feature_tmp = [] lable_tmp = [] lines = line.strip().split("\t") feature_tmp.append(1) # 偏置项 for i in range(len(lines) - 1): feature_tmp.append(float(lines[i])) lable_tmp.append(float(lines[-1])) feature_data.append(feature_tmp) #append() 方法用于在列表末尾添加新的对象。 label_data.append(lable_tmp) f.close() # 关闭文件 return np.mat(feature_data), np.mat(label_data) def load_weight(w): '''导入LR模型 input: w(string)权重所在的文件位置 output: np.mat(w)(mat)权重的矩阵 ''' f = open(w) w = [] for line in f.readlines(): lines = line.strip().split("\t") w_tmp = [] for x in lines: w_tmp.append(float(x)) w.append(w_tmp) f.close() return np.mat(w) if __name__ == "__main__": # 1、导入训练数据 print ("---------- 1.load data ------------") feature, label = load_data("data.txt") #提取原数据、标签 w = load_weight("weights") w=w.T Ypic = feature * w x_1 = feature[:,1] #横坐标 x_2 = feature[:,2] #纵坐标 for i in range(0, 199): if (label[i,:] == 0): plt.plot(x_1[i,:],x_2[i,:],c = 'r',marker = 'o') #作标签为0的数据 else: plt.plot(x_1[i,:],x_2[i,:],c = 'g',marker = 'o') #作标签为0的数据 x =np.mat(np.linspace( 0.0,10,100)) y = (-w[0]-w[1]*x)/w[2] #注意点2, 已知a,b,c, 根据ax+by+c=0作图 plt.plot(x,y,c = 'b',marker = 'o') plt.show() #显示所有图表

参考文献
[1] 赵志勇. Python机器学习算法[M]. 北京:电子工业出版社,2017.
[2] 李航. 统计学习方法[M]. 北京:清华大学出版社,2012.
[3] 周志华. 机器学习[M]. 北京:清华大学出版社,2016.
附录
数据集下载:
链接:https://pan.baidu.com/s/13awWgR7NIBjme0oM7UXzig
提取码:li2w




