CNN 批归一化（Batch Normalization）

批归一化方法方法（Batch Normalization，BatchNorm）是由Ioffe和Szegedy于2015年提出的，已被广泛应用在深度学习中，其目的是对神经网络中间层的输出进行标准化处理，使得中间层的输出更加稳定。

通常我们会对神经网络的数据进行标准化处理，处理后的样本数据集满足均值为0，方差为1的统计分布，这是因为当输入数据的分布比较固定时，有利于算法的稳定和收敛。对于深度神经网络来说，由于参数是不断更新的，即使输入数据已经做过标准化处理，但是对于比较靠后的那些层，其接收到的输入仍然是剧烈变化的，通常会导致数值不稳定，模型很难收敛。BatchNorm能够使神经网络中间层的输出变得更加稳定，并有如下三个优点：

使学习快速进行（能够使用较大的学习率）

降低模型对初始值的敏感性

从一定程度上抑制过拟合

BatchNorm主要思路是在训练时按mini-batch为单位，对神经元的数值进行归一化，使数据的分布满足均值为0，方差为1。具体计算过程如下：

1. 计算mini-batch内样本的均值

 

 

 

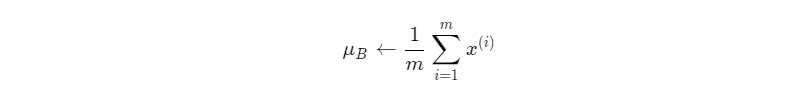
其中x(i)表示mini-batch中的第i个样本。

例如输入mini-batch包含3个样本，每个样本有2个特征，分别是：

 

 

 

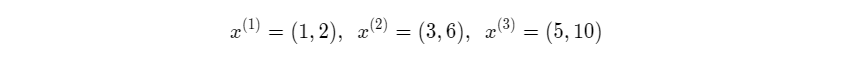
对每个特征分别计算mini-batch内样本的均值：

 

 

 

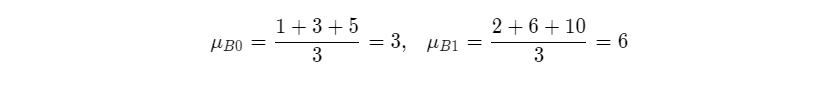
则样本均值是:

 

 

 

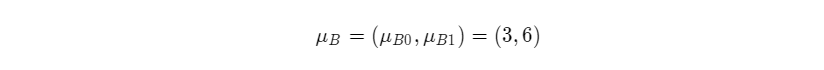
（说了那么多就是计算均值）

 

 

2. 计算mini-batch内样本的方差

 

 

 

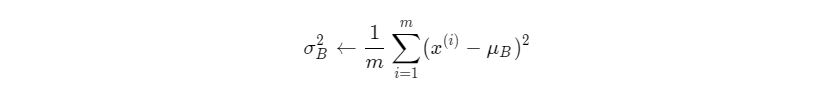
上面的计算公式先计算一个批次内样本的均值μB和方差σ2B，然后再对输入数据做归一化，将其调整成均值为0，方差为1的分布。

对于上述给定的输入数据x(1),x(2),x(3)，可以计算出每个特征对应的方差：

 

 

 

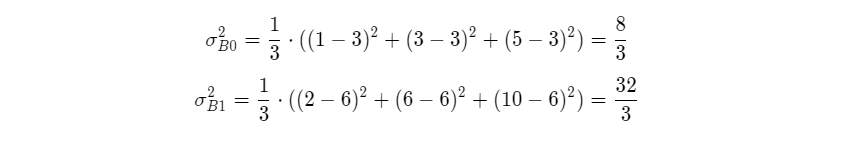
则样本方差是：

 

 

 

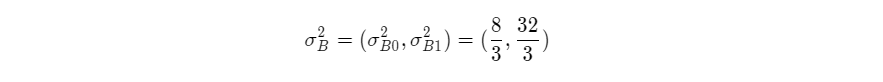
（一般以同属性为一组，直接求方差，上述计算都是脑海中的高中数学）

 

 

3. 计算标准化之后的输出

 

 

 

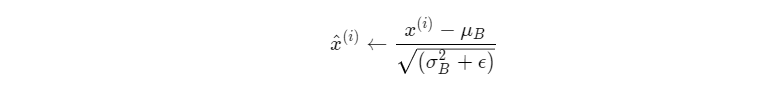
其中ϵ是一个微小值（例如1e−7），其主要作用是为了防止分母为0。

对于上述给定的输入数据x(1),x(2),x(3)，可以计算出标准化之后的输出：

 

 

 

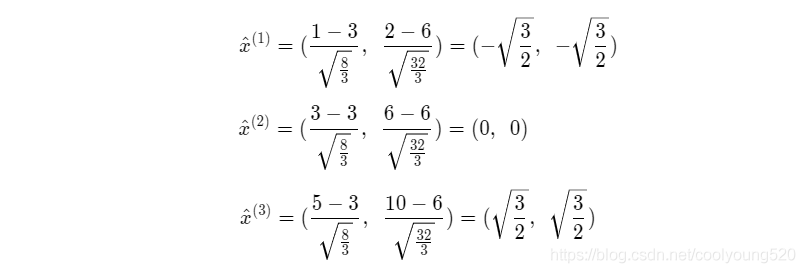
读者可以自行验证由x^(1),x^(2),x^(3)构成的mini-batch，是否满足均值为0，方差为1的分布。
如果强行限制输出层的分布是标准化的，可能会导致某些特征模式的丢失，所以在标准化之后，BatchNorm会紧接着对数据做缩放和平移。

 

 

 

其中γ和β是可学习的参数，可以赋初始值γ=1,β=0，在训练过程中不断学习调整。

上面列出的是BatchNorm方法的计算逻辑，下面针对两种类型的输入数据格式分别进行举例。飞桨支持输入数据的维度大小为2、3、4、5四种情况，这里给出的是维度大小为2和4的示例。

示例一： 当输入数据形状是[N,K]时，一般对应全连接层的输出，示例代码如下所示。
这种情况下会分别对K的每一个分量计算N个样本的均值和方差，数据和参数对应如下：

输入 x, [N, K]
输出 y, [N, K]
均值 μB，[K, ]
方差 σ2B，[K, ]
缩放参数γ，[K, ]
平移参数β，[K, ]
 

# 输入数据形状是 [N, K]时的示例
import numpy as np

import paddle
import paddle.fluid as fluid
from paddle.fluid.dygraph.nn import BatchNorm
# 创建数据
data = np.array([[1,2,3], [4,5,6], [7,8,9]]).astype('float32')
# 使用BatchNorm计算归一化的输出
with fluid.dygraph.guard():
# 输入数据维度[N, K]，num_channels等于K
bn = BatchNorm(num_channels=3) 
x = fluid.dygraph.to_variable(data)
y = bn(x)
print('output of BatchNorm Layer: \n {}'.format(y.numpy()))

# 使用Numpy计算均值、方差和归一化的输出
# 这里对第0个特征进行验证
a = np.array([1,4,7])
a_mean = a.mean()
a_std = a.std()
b = (a - a_mean) / a_std
print('std {}, mean {}, \n output {}'.format(a_mean, a_std, b))

# 建议读者对第1和第2个特征进行验证，观察numpy计算结果与paddle计算结果是否一致
output of BatchNorm Layer: 
[[-1.2247438 -1.2247438 -1.2247438]
[ 0. 0. 0. ]
[ 1.2247438 1.2247438 1.2247438]]
std 4.0, mean 2.449489742783178, 
output [-1.22474487 0. 1.22474487]

 

示例二： 当输入数据形状是[N,C,H,W]时， 一般对应卷积层的输出，示例代码如下所示。
这种情况下会沿着C这一维度进行展开，分别对每一个通道计算N个样本中总共N×H×W个像素点的均值和方差，数据和参数对应如下：

输入 x, [N, C, H, W]
输出 y, [N, C, H, W]
均值 μB，[C, ]
方差 σ2B​,  [C, ]
缩放参数γ, [C, ]
平移参数β, [C, ]
小窍门：

可能有读者会问：“BatchNorm里面不是还要对标准化之后的结果做仿射变换吗，怎么使用Numpy计算的结果与BatchNorm算子一致？” 这是因为BatchNorm算子里面自动设置初始值γ=1,β=0，这时候仿射变换相当于是恒等变换。在训练过程中这两个参数会不断的学习，这时仿射变换就会起作用。

 

# 输入数据形状是[N, C, H, W]时的batchnorm示例
import numpy as np

import paddle
import paddle.fluid as fluid
from paddle.fluid.dygraph.nn import BatchNorm

# 设置随机数种子，这样可以保证每次运行结果一致
np.random.seed(100)
# 创建数据
data = np.random.rand(2,3,3,3).astype('float32')
# 使用BatchNorm计算归一化的输出
with fluid.dygraph.guard():
# 输入数据维度[N, C, H, W]，num_channels等于C
bn = BatchNorm(num_channels=3)
x = fluid.dygraph.to_variable(data)
y = bn(x)
print('input of BatchNorm Layer: \n {}'.format(x.numpy()))
print('output of BatchNorm Layer: \n {}'.format(y.numpy()))

# 取出data中第0通道的数据，
# 使用numpy计算均值、方差及归一化的输出
a = data[:, 0, :, :]
a_mean = a.mean()
a_std = a.std()
b = (a - a_mean) / a_std
print('channel 0 of input data: \n {}'.format(a))
print('std {}, mean {}, \n output: \n {}'.format(a_mean, a_std, b))

# 提示：这里通过numpy计算出来的输出
# 与BatchNorm算子的结果略有差别，
# 因为在BatchNorm算子为了保证数值的稳定性，
# 在分母里面加上了一个比较小的浮点数epsilon=1e-05
input of BatchNorm Layer: 
[[[[0.54340494 0.2783694 0.4245176 ]
[0.84477615 0.00471886 0.12156912]
[0.67074907 0.82585275 0.13670659]]

[[0.5750933 0.89132196 0.20920213]
[0.18532822 0.10837689 0.21969749]
[0.9786238 0.8116832 0.17194101]]

[[0.81622475 0.27407375 0.4317042 ]
[0.9400298 0.81764936 0.33611196]
[0.17541045 0.37283206 0.00568851]]]


[[[0.25242636 0.7956625 0.01525497]
[0.5988434 0.6038045 0.10514768]
[0.38194343 0.03647606 0.89041156]]

[[0.98092085 0.05994199 0.89054596]
[0.5769015 0.7424797 0.63018394]
[0.5818422 0.02043913 0.21002658]]

[[0.5446849 0.76911515 0.25069523]
[0.2858957 0.8523951 0.9750065 ]
[0.8848533 0.35950786 0.59885895]]]]
output of BatchNorm Layer: 
[[[[ 0.4126078 -0.46198368 0.02029109]
[ 1.4071034 -1.3650038 -0.97940934]
[ 0.832831 1.344658 -0.9294571 ]]

[[ 0.2520175 1.2038351 -0.84927964]
[-0.9211378 -1.1527538 -0.8176896 ]
[ 1.4666051 0.96413004 -0.961432 ]]

[[ 0.9541142 -0.9075856 -0.36629617]
[ 1.37925 0.9590063 -0.6945517 ]
[-1.2463869 -0.5684581 -1.8291974 ]]]


[[[-0.5475932 1.2450331 -1.3302356 ]
[ 0.5955492 0.6119205 -1.0335984 ]
[-0.12019944 -1.2602081 1.5576957 ]]

[[ 1.473519 -1.2985382 1.2014993 ]
[ 0.25745988 0.7558342 0.41783488]
[ 0.27233088 -1.4174379 -0.8467981 ]]

[[ 0.02166975 0.79234385 -0.98786545]
[-0.86699003 1.0783203 1.4993572 ]
[ 1.1897788 -0.6142123 0.20769882]]]]
channel 0 of input data: 
[[[0.54340494 0.2783694 0.4245176 ]
[0.84477615 0.00471886 0.12156912]
[0.67074907 0.82585275 0.13670659]]

[[0.25242636 0.7956625 0.01525497]
[0.5988434 0.6038045 0.10514768]
[0.38194343 0.03647606 0.89041156]]]
std 0.4183686077594757, mean 0.3030227720737457, 
output: 
[[[ 0.41263014 -0.46200886 0.02029219]
[ 1.4071798 -1.3650781 -0.9794626 ]
[ 0.8328762 1.3447311 -0.92950773]]

[[-0.54762304 1.2451009 -1.3303081 ]
[ 0.5955816 0.61195374 -1.0336547 ]
[-0.12020606 -1.2602768 1.5577804 ]]]
 

 

- 预测时使用BatchNorm

（预测用训练时保存的相应结果）

上面介绍了在训练过程中使用BatchNorm对一批样本进行归一化的方法，但如果使用同样的方法对需要预测的一批样本进行归一化，则预测结果会出现不确定性。

例如样本A、样本B作为一批样本计算均值和方差，与样本A、样本C和样本D作为一批样本计算均值和方差，得到的结果一般来说是不同的。那么样本A的预测结果就会变得不确定，这对预测过程来说是不合理的。解决方法是在训练过程中将大量样本的均值和方差保存下来，预测时直接使用保存好的值而不再重新计算。实际上，在BatchNorm的具体实现中，训练时会计算均值和方差的移动平均值。在飞桨中，默认是采用如下方式计算：

 

 

 

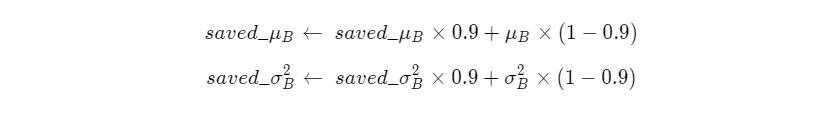
在训练过程的最开始将saved_μB和saved_σ2B​设置为0，每次输入一批新的样本，计算出μB和σ2B，然后通过上面的公式更新saved_μB​和saved_σ2B，在训练的过程中不断的更新它们的值，并作为BatchNorm层的参数保存下来。预测的时候将会加载参数saved_μB​和saved_σ2B​，用他们来代替μB​和σ2B​。
————————————————
版权声明：本文为CSDN博主「aiAIman」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/coolyoung520/article/details/109075379