SVM求解 SMO 算法概述

SMO 是由 Platt 在 1998 年提出的、针对软间隔最大化 SVM 对偶问题求解的一个算法，其基本思想很简单：在每一步优化中，挑选出诸多参数（ $\alpha_k(k=1,2,...,N)$ ）中的两个参数（ $\alpha_i$ 、 $\alpha_j$ ）作为“真正的参数”，其余参数都视为常数，从而问题就变成了类似于二次方程求最大值的问题，从而我们就能求出解析解

具体而言，SMO 要解决的是如下对偶问题：

$\max_\alpha L(\alpha)=-\frac12\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j) + \sum_{i=1}^N\alpha_i$

使得对 $i=1,...,N$ 、都有

$\sum_{i=1}^N\alpha_iy_i=0$ 、 $0\le\alpha_i\le C$

其大致求解步骤则可以概括如下：

选出 $\alpha_1,\alpha_2,...,\alpha_N$ 中“最不好的”两个参数 $\alpha_i$ 、 $\alpha_j$
只把 $\alpha_i$ 、 $\alpha_j$ 视为参数并把其余的 $\alpha_k$ 视为常数，于是最大化 $L(\alpha)$ 就变成了以 $\alpha_i$ 、 $\alpha_j$ 为参数的二次规划问题，从而可以直接对其进行求解；但是，注意到 $\alpha_i$ 、 $\alpha_j$ 需满足 $\sum_{i=1}^N\alpha_iy_i=0$ 和 $0\le\alpha_i$ 、 $\alpha_j\le C$ ，所以求完解后需要检查是否满足约束；如不满足，则进行调整

KKT 条件

先来看如何选取参数。在 SMO 算法中，我们是依次选取参数的：

选出违反 KKT 条件最严重的样本点、以其对应的参数作为第一个参数
第二个参数的选取有一种比较繁复且高效的方法，但对于一个朴素的实现而言、第二个参数即使随机选取也无不可

这里就有了一个叫 KKT 条件的东西，其详细的陈列会放在文末，这里就仅简要的说明一下。具体而言，对于已有的模型 $f(x)=w\cdot x + b$ 来说， $\alpha_i$ 及其对应样本 $(x_i,y_i)$ 的 KKT 条件为：

$\begin{align} \alpha_i=0&\Leftrightarrow y_if(x_i)>1 \\ 0<\alpha_i<C&\Leftrightarrow y_if(x_i)=1 \\ \alpha_i = C&\Leftrightarrow y_if(x_i)<1 \end{align}$

注意我们之前提过样本到超平面的函数间隔为 $y(w\cdot x+b)$ ，所以上述 KKT 条件可以直观地叙述为：

$\alpha_i=0\Leftrightarrow$ 样本离间隔超平面比较远
$0<\alpha_i<C\Leftrightarrow$ 样本落在间隔超平面上
$\alpha_i=C\Leftrightarrow$ 样本在间隔超平面以内

【注意：这里的间隔超平面即为满足方程 $y(w\cdot x+b)=1$ 的平面；由于 $y$ 可以取正负一两个值，所以间隔超平面会有两个—— $w\cdot x+b=1$ 和 $w\cdot x+b=-1$ 。而分类超平面则是满足 $w\cdot x+b=0$ 的平面，需要将它和间隔超平面加以区分】

可以以一张图来直观理解这里提到的诸多概念：

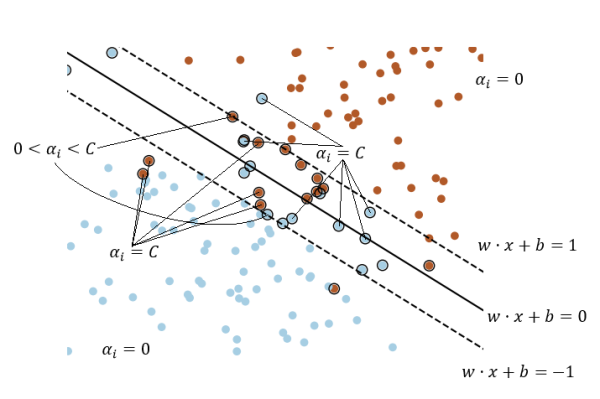
（画得有点乱，见谅……）

图中外面有个黑圆圈的其实就是传说中的“支持向量”，其定义会在文末给出

那么我们到底应该如何刻画“违反 KKT 条件”这么个东西呢？从直观上来说，我们可以有这么一种简单有效的定义：

计算三份“差异向量” $c^{(k)}=(c^{(k)}_1,c^{(k)}_2,...,c^{(k)}_N)^T\ \ (k=1,2,3)$ ，其中第 $k$ 份对应于三个 KKT 条件中的第 $k$ 个，且 $c^{(k)}_i=y_if(x_i)-1\ \ (i=1,2,...,N)$
针对不同的 KKT 条件，将 $c^{(k)}$ 的某些位置 $c^{(k)}_i$ 置为 0。具体而言：

对第一个 KKT 条件 $\alpha_i=0\Leftrightarrow y_if(x_i)>1\Leftrightarrow c^{(1)}_i>0$ 而言，满足以下两种情况的 $c^{(1)}_i$ 将应该置为 0：

$\alpha_i>0$ 且 $c^{(1)}_i\le0$
$\alpha_i=0$ 且 $c^{(1)}_i>0$

对第二个 KKT 条件 $0<\alpha_i<C\Leftrightarrow y_if(x_i)=1\Leftrightarrow c^{(2)}_i=0$ 而言则是：

（ $\alpha_i=0$ 或 $\alpha_i=C$ ）且 $c^{(2)}_i\ne0$
$0<\alpha_i<C$ 且 $c^{(2)}_i=0$

对第三个 KKT 条件 $\alpha_i = C\Leftrightarrow y_if(x_i)<1\Leftrightarrow c^{(3)}_i<0$ 亦同理：

$\alpha_i<C$ 且 $c^{(3)}_i\ge0$
$\alpha_i=C$ 且 $c^{(3)}_i<0$

最后则可以简单的将三份差异向量的平方相加来作为“损失”，从而直接选出使该损失最大的 $\alpha_i$ 作为 SMO 的第一个参数即可。具体而言：
$i=\arg\max_i\left\{ c^{(1)^2}_i + c^{(2)^2}_i + c^{(3)^2}_i | i=1,2,...,N\right\}$

得益于 Numpy 强大的 Fancy Indexing，上述置 0 的实现非常好写（？？？）：

# 得到 alpha > 0 和 alpha < C 的 mask
con1 = alpha > 0
con2 = alpha < C
# 算出“差异向量”并拷贝成三份
err1 = y * y_pred - 1
err2 = err1.copy()
err3 = err1.copy()
# 依次根据三个 KKT 条件，将差异向量的某些位置设为 0
# 不难看出为了直观、我做了不少重复的运算，所以这一步是可以优化的
err1[(con1 & (err1 <= 0)) | (~con1 & (err1 > 0))] = 0
err2[((~con1 | ~con2) & (err2 != 0)) | ((con1 & con2) & (err2 == 0))] = 0
err3[(con2 & (err3 >= 0)) | (~con2 & (err3 < 0))] = 0
# 算出平方和并取出使得“损失”最大的 idx
err = err1 ** 2 + err2 ** 2 + err3 ** 2
idx = np.argmax(err)

第二个参数则可以简单地随机选取，虽然这不是特别好，但效果已然不错，而且不仅实现起来更简便、运行起来也更快（其实就是我太懒）（喂）。具体代码如下：

idx = np.random.randint(len(self._y))
# 这里的 idx1 是第一个参数对应的 idx
while idx == idx1:
    idx = np.random.randint(len(self._y))
return idx

至于 SMO 算法的第二步，正如前文所说，它的本质就是一个带约束的二次规划，虽然求解过程可能会比较折腾，但其实难度不大。具体步骤会放在文末，这里就暂时按下

SMO 的效果

仍是先看看螺旋线数据集上的训练过程：

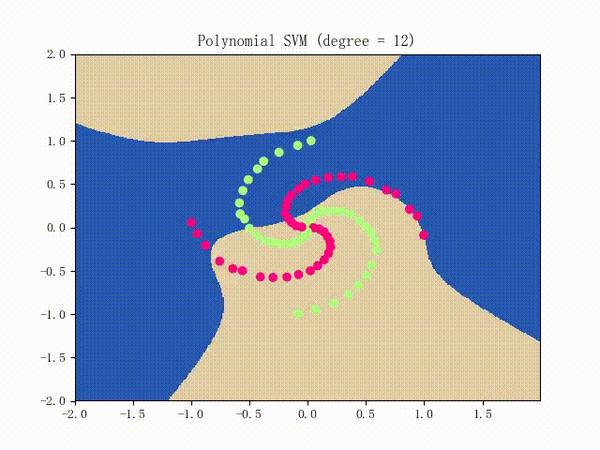
略显纠结，不过还是不错的

接下来看看蘑菇数据集上的表现；单就这个数据集而言，我们实现的朴素 SVM 和 sklearn 中的 SVM 表现几乎是一致的（在使用 RBF 核时），比较具有代表性的训练曲线则如下图所示：

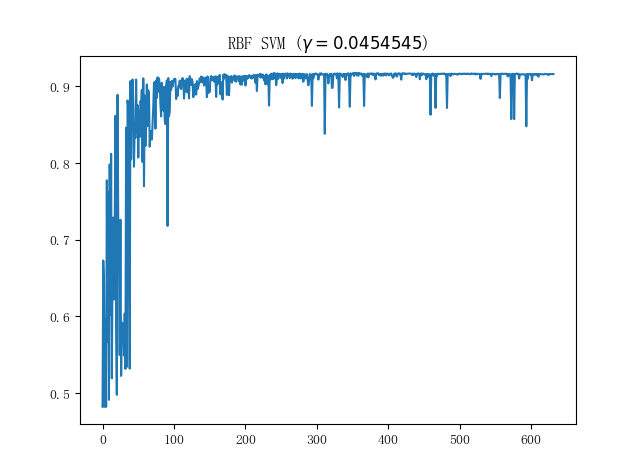也算是符合 SMO 这种每次只取两个参数进行更新的训练方法的直观

相关数学理论

1）KKT 条件的详细陈列

注意到原始问题为

$\min_{w,b,\xi}L(w,b,\xi)=\frac12\|w\|^2+C\sum_{i=1}^N\xi_i$ ，使得 $\xi^*\ge0$ 、 $y_i(w\cdot x_i+b)\ge1-\xi_i$ （不妨称这两个约束为原始约束）

所以其拉格朗日算子法对应的式子为

$L=L(w,b,\xi,\alpha,\beta)=\frac12\|w\|^2+C\sum_{i=1}^N\xi_i-\sum_{i=1}^N\alpha_i[y_i(w\cdot x_i+b)-1+\xi_i]-\sum_{i=1}^N\beta_i\xi_i$

于是 KKT 条件的其中四个约束即为（不妨设最优解为 $w^*$ 、 $b^*$ 、 $\xi^*$ 、 $\alpha^*$ 和 $\beta^*$ ）：

$\alpha_i^*\ge0,\beta_i^*\ge0$ （这是拉格朗日乘子法自身的要求）
$\xi_i^*\ge0$ 、 $y_i(w^*\cdot x_i+b^*)-1+\xi_i^*\ge0$ （此即原始约束）
$\alpha_i^*[y_i(w^*\cdot x_i+b^*)-1+\xi_i^*]=0$ （换句话说， $\alpha_i^*$ 和 $y_i(w^*\cdot x_i+b)-1+\xi_i^*$ 中必有一个为 0）

该等式有着很好的直观：设想它们同时不为 0，则必有 $y_i(w^*\cdot x_i+b)-1+\xi_i^*>0$ （注意原始约束）、从而 $\alpha_i^*[y_i(w^*\cdot x_i+b^*)-1+\xi_i^*]\ge0$ ，等号当且仅当 $\alpha_i=0$ 时取得。然而由于 $\alpha_i^*\ne0$ ，所以若将 $\alpha_i$ 取为 0、则上述 $L$ 将会变大。换句话说，将参数 $\alpha_i$ 取为 0 将会使得目标函数比参数取 $\alpha_i^*$ 时的目标函数要大，这与 $\alpha_i^*$ 的最优性矛盾

$\beta_i^*\xi_i^*=0$ （换句话说， $\beta_i^*$ 和 $\xi_i^*$ 中必有一个为 0，理由同上）

从而原始问题转为 $\min_{w,b}\max_\alpha L$ ；而对偶问题的实质，其实就是将原始问题 $\min_{w,b}\max_\alpha L$ 转为 $\max_\alpha\min_{w,b} L$ 。在求解 $\nabla_wL=\nabla_bL=\nabla_\xi L=0$ 后，可以得到如下对偶问题：

$\max_\alpha L(\alpha)=-\frac12\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j) + \sum_{i=1}^N\alpha_i$ ，使得对 $i=1,...,N$ 、都有 $\sum_{i=1}^N\alpha_iy_i=0$ 、 $0\le\alpha_i\le C$

（虽然这些在 Python · SVM（二）· LinearSVM 中介绍过，不过为了连贯性，这里还是再介绍一遍）

于是，最优解自然需要满足这么个条件：

$\nabla_wL(w^*,b^*,\xi^*,\alpha^*,\beta^*)=\nabla_bL(w^*,b^*,\xi^*,\alpha^*,\beta^*)=\nabla_\xi L(w^*,b^*,\xi^*,\alpha^*,\beta^*)=0$

这个条件即是最后一个 KKT 条件

2）何谓“支持向量”

为方便说明，这里再次放出上文给出过的图：

图中带黑圈的样本点即是支持向量，数学上来说的话，就是 $\alpha_i>0$ 对应的样本点即是支持向量。从图中不难看出，支持向量从直观上来说，就是比较难分的样本点

此外，支持向量之所以称之为“支持”向量，是因为在理想情况下，仅利用支持向量训练出来的模型和利用所有样本训练出来的模型是一致的。这从直观上是好理解的，粗略的证明则可以利用其定义来完成：非支持向量的样本对应着 $\alpha_i=0$ ，亦即它对最终模型—— $f(x)=\sum_{i=1}^N\alpha_iy_i(x_i\cdot x)+b$ 没有丝毫贡献，所以可以直接扔掉

3）带约束的二次规划求解方法

不妨设我们选取出来的两个参数就是 $\alpha_1$ 和 $\alpha_2$ ，那么问题的关键就在于如何把 $\alpha_1$ 和 $\alpha_2$ 相关的东西抽取出来并把其它东西扔掉

注意到我们的对偶问题为

$\max_\alpha L(\alpha)=-\frac12\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j) + \sum_{i=1}^N\alpha_i$ ，使得对 $i=1,...,N$ 、都有 $\sum_{i=1}^N\alpha_iy_i=0$ 、 $0\le\alpha_i\le C$

且我们在 Python · SVM（一）· 感知机的最后介绍过 Gram 矩阵：

$G=(x_i\cdot x_j)_{N\times N}$

所以 $L$ 就可以改写为 $L(\alpha)=-\frac12\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_jG_{ij}+\sum_{i=1}^N\alpha_i$

把和 $\alpha_1$ 、 $\alpha_2$ 无关的东西扔掉之后， $L$ 可以化简为：

$L(\alpha)=-\frac12(G_{11}\alpha_1^2+2y_1y_2G_{12}\alpha_1\alpha_2+G_{22}\alpha_2^2)-\left(y_1\alpha_1\sum_{i=3}^Ny_i\alpha_iG_{i1}+y_2\alpha_2\sum_{i=3}^Ny_i\alpha_iG_{i2}\right)+(\alpha_1+\alpha_2)$

约束条件则可以化简为对 $i=1$ 和 $i=2$ ，都有 $y_1\alpha_1+y_2\alpha_2=-\sum_{i=3}^Ny_i\alpha_i=c$ 、 $0\le\alpha_i\le C$ ，其中 $c$ 是某个常数

而带约束的二次规划求解过程也算简单：只需先求出无约束下的最优解，然后根据约束“裁剪”该最优解即可

无约束下的求解过程其实就是求偏导并令其为 0。以 $\alpha_1$ 为例，注意到

$y_1\alpha_1+y_2\alpha_2=c\Rightarrow\alpha_2=\frac c{y_2}-\frac{y_1}{y_2}\alpha_1$

令 $c^*=\frac c{y_2},\ \ s=y_1y_2$ ，则 $c^*$ 亦是常数，且由于 $y_1$ 、 $y_2$ 都只能取正负 1，故不难发现 $\frac{y_2}{y_1}=\frac{y_1}{y_2}=s$ ，从而 $\alpha_2=c^*-s\alpha_1\Rightarrow\frac{\partial\alpha_2}{\partial\alpha_1}=-s$

于是

$\begin{align} \frac{\partial L}{\partial\alpha_1}=&-G_{11}\alpha_1-y_1y_2G_{12}(\alpha_2+\alpha_1\frac{\partial\alpha_2}{\partial\alpha_1})-G_{22}\alpha_2\frac{\partial\alpha_2}{\partial\alpha_1} \\ &-y_1\sum_{i=3}^Ny_i\alpha_iG_{i1}-y_2\frac{\partial\alpha_2}{\partial\alpha_1}\sum_{i=3}^Ny_i\alpha_iG_{i2}+1 \\ =&-G_{11}\alpha_1-sG_{12}(c^*-s\alpha_1-\alpha_1\cdot s)-G_{22}(c^*-s\alpha_1)\cdot(-s) \\ &-y_1\sum_{i=3}^Ny_i\alpha_iG_{i1}+sy_2\sum_{i=3}^Ny_i\alpha_iG_{i2}+\left(\frac{\partial\alpha_2}{\partial\alpha_1}+1\right) \end{align}$

考虑到 $s^2=1$ 、 $sy_2=y_1$ 、Gram 矩阵是对称阵、且模型在第 $k$ 个样本 $x_k$ 处的输出为 $f(x_k)=\sum_{i=1}^N\alpha_iy_i(x_i\cdot x_k)+b=\sum_{i=1}^N\alpha_iy_iG_{ik}+b$ ，从而可知

$\begin{align} \frac{\partial L}{\partial\alpha_1}=&-G_{11}\alpha_1-sG_{12}c^*+2G_{12}\alpha_1+sG_{22}c^*-G_{22}\alpha_1 \\ &-y_1[f(x_1)-y_1\alpha_1G_{11}-y_2\alpha_2G_{21}] \\ &+y_1[f(x_2)-y_1\alpha_1G_{12}-y_2\alpha_2G_{22}] +(1-s) \end{align}$

令 $v_i=(f(x_i)-b)-y_1\alpha_1G_{1i}-y_2\alpha_2G_{2i}\ \ (i=1,2)$ ，则

$\frac{\partial L}{\partial\alpha_1}=-(G_{11}-2G_{12}+G_{22})\alpha_1-sc^*(G_{12}-G_{22})-y_1(v_1-v_2)+(1-s)$

于是

$\begin{align} \frac{\partial L}{\partial\alpha_1}=0\Rightarrow\alpha_1&=-\frac{sc^*(G_{12}-G_{22})+y_1(v_1-v_2)-(1-s)}{G_{11}-2G_{12}+G_{22}} \\ &=-\frac{y_1[y_2c^*(G_{12}-G_{22})+(v_1-v_2)-(y_1-y_2)]}{G_{11}-2G_{12}+G_{22}} \end{align}$

注意到 $c^*=s\alpha_1+\alpha_2$ ，从而

$y_2c^*(G_{12}-G_{22})=y_2(s\alpha_1+\alpha_2)(G_{12}-G_{22})=(y_1\alpha_1+y_2\alpha_2)(G_{12}-G_{22})$

令 $dG=G_{11}-2G_{12}+G_{22}$ 、 $e_i=f(x_i)-y_i\ \ (i=1,2)$ ，则

$y_2c^*(G_{12}-G_{22})+(v_1-v_2)-(y_2+y_1)=... =e_1 - e_2 - y_1\alpha_1dG$

从而

$\alpha_1^{new,raw}=\alpha_1^{old}-\frac{y_1(e_1-e_2)}{dG}$

接下来就要对其进行裁剪了。注意到我们的约束为

$0\le\alpha_i\le C$ 、 $\alpha_1y_1+\alpha_2y_2$ 为常数

所以我们需要分情况讨论 $\alpha_1$ 的下、上界

当 $y_1,y_2$ 异号（ $y_1y_2=-1$ ）时，可知 $\alpha_1-\alpha_2$ 为常数、亦即
$\alpha_1^{new}-\alpha_2^{new}=\alpha_1^{old}-\alpha_2^{old}\Rightarrow\alpha_2^{new}=\alpha_1^{new}-(\alpha_1^{old}-\alpha_2^{old})$
结合 $0\le\alpha_2\le C$ ，可知：

$\alpha_1^{new}$ 不应小于 $\alpha_1^{old}-\alpha_2^{old}$ ，否则 $\alpha_2$ 将小于 0
$\alpha_1^{new}$ 不应大于 $C+\alpha_1^{old}-\alpha_2^{old}$ ，否则 $\alpha_2$ 将大于 C

当 $y_1,y_2$ 同号（ $y_1y_2=1$ ）时，可知 $\alpha_1+\alpha_2$ 为常数、亦即
$\alpha_1^{new}+\alpha_2^{new}=\alpha_1^{old}+\alpha_2^{old}\Rightarrow\alpha_2^{new}=(\alpha_1^{old}+\alpha_2^{old}) - \alpha_1^{new}$
结合 $0\le\alpha_2\le C$ ，可知：

$\alpha_1^{new}$ 不应小于 $\alpha_1^{old}+\alpha_2^{old}-C$ ，否则 $\alpha_2$ 将大于 C
$\alpha_1^{new}$ 不应大于 $\alpha_1^{old}+\alpha_2^{old}$ ，否则 $\alpha_2$ 将小于 0

综上可知

$\alpha_1^{new}$ 的下界为 $U=\left\{\begin{aligned} \max\{0,\alpha_1^{old}-\alpha_2^{old}\}\ \ &y_1y_2=-1 \\ \max\{0,\alpha_1^{old}+\alpha_2^{old}-C\}\ \ &y_1y_2=1 \end{aligned} \right.$
$\alpha_1^{new}$ 的上界为 $V=\left\{\begin{aligned} \min\{C,C+\alpha_1^{old}-\alpha_2^{old}\}\ \ &y_1y_2=-1 \\ \max\{C,\alpha_1^{old}+\alpha_2^{old}\}\ \ &y_1y_2=1 \end{aligned} \right.$

那么直接做一个 clip 即可得到更新后的 $\alpha_1$ ：

alpha1_new = np.clip(alpha1_new_raw, u, v)

注意由于我们要保持 $\alpha_1y_1+\alpha_2y_2$ 为常数，所以（注意 $\frac{y_1}{y_2}=y_1y_2$ ）

$\begin{align} \alpha_2^{new}&=\frac1{y_2}(\alpha_1^{old}y_1+\alpha_2^{old}y_2-\alpha_1^{new}y_1) \\ &=\alpha_2^{old}+y_1y_2(\alpha_1^{old}-\alpha_1^{new}) \end{align}$

综上所述，我们就完成了一次参数的更新，之后就不断地更新直至满足停机条件即可

此外，我在 Python · SVM（三）· 核方法这篇文章中提到过，对 SVM 的对偶形式应用核方法会非常自然。表现在 SMO 上的话就是，我们可以通过简单粗暴地将核矩阵 $K$ 代替 Gram 矩阵 $G$ 来完成核方法的应用。直观地说，我们只需将上面所有出现过的 $G$ 都换成 $K$ 就行了

至此，SVM 算法的介绍就大致告一段落了。我们从感知机出发，依次介绍了“极大梯度法”、MBGD（Batch 梯度下降）法、核方法和 SMO 算法；虽然都有点浅尝辄止的味道，但覆盖的东西……大概还是挺多的

posted @ 2021-02-23 20:06 lvdongjie-avatarx 阅读(476) 评论(0) 编辑收藏举报

刷新页面返回顶部

lvdongjie-avatarx

此博客专攻人工智能。

SVM求解 SMO 算法概述

KKT 条件

SMO 的效果

相关数学理论

公告