集成学习-Boosting-GBDT提升-XGBoost
前言
XGBoost是boosting算法的其中一种。Boosting算法的思想是将许多弱分类器集成在一起形成一个强分类器。XGBoost是一种提升树模型,它是将许多树模型集成在一起,形成一个很强的分类器,所用到的树模型则是CART回归树模型。
CART
CART回归树是假设树的结构为二叉树,通过不断将特征进行分裂去完成整个树的构建。比如当前树结点是基于第 个特征值进行分裂的,设该特征值小于
的样本划分为左子树,大于
的样本划分为右子树,即
。其实质就是在该特征维度上对样本空间进行划分,这种划分是非常复杂度,通常是NP难问题。因此,在决策树模型中是使用启发式方法解决特征划分问题。
典型CART回归树模型的目标函数为: ,我们结合求解最优的切分特征
和最优的切分点
,那么目标函数就转化为求解如下式子:
所以,我们只要遍历所有特征的的所有切分点,就能找到最优的切分特征和切分点。最终得到一棵回归树。
XGBoost算法原理
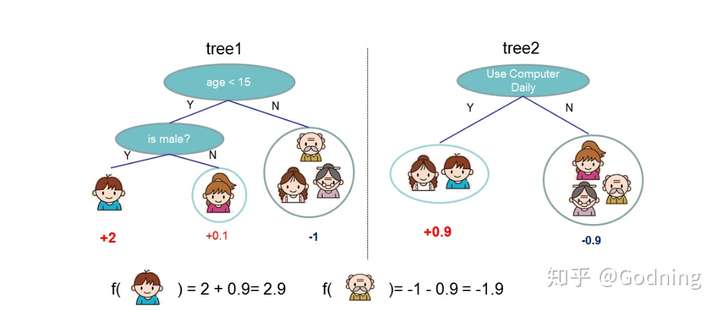
XGBoost算法思想就是不断地添加树,不断地进行特征分裂来完成一棵树的构建。每次添加一个树,实际上是学习一个新函数,去拟合上次预测的残差。我们训练完成时会得到 棵树 。当我们要预测一个样本的分数时,根据这个样本的特征,在每棵树中会落到对应的一个叶子节点,每个叶子节点就对应一个分数,最后只需要将每棵树对应的分数加起来就是该样本的预测值。如:
注: 为叶子节点
的分数,
为其中一棵回归树 。
如下图所示,训练出了2棵决策树,小孩的预测分数就是两棵树中小孩所落到的结点的分数相加。爷爷的预测分数同理。
XGBoost损失函数
XGBoost目标函数定义为: ,目标函数由两部分构成,第一部分
用来衡量预测分数和真实分数的差距,另一部分
则是正则化项。正则化项同样包含两部分,
。
表示叶子结点的个数,
表示叶子节点的分数。
可以控制叶子结点的个数,
可以制叶子节点的分数不会过大,防止过拟合。
正如第二部分所说,新生成的树是要拟合上次预测的残差的,即当生成 棵树后,预测分数可以写成:
,同时,可以将目标函数改写成:
,很明显,我们接下来就是要去找到一个
能够最小化目标函数。XGBoost的想法是利用其在
处的泰勒二阶展开近似它。即
。所以,目标函数近似为:
,其中为
一阶导数,
为二阶导数:
。式子中的
和
是一阶和二阶梯度。
以上这就是XGboost的特点:通过这种近似,可以自行定义一些损失函数(例如,平方损失,逻辑损失),只需要保证二阶可导即可。由于前 棵树的预测分数与的残差对目标函数优化不影响,可以直接去掉。简化目标函数为:
上式是将每个样本的损失函数值加起来,我们知道,每个样本都最终会落到一个叶子结点中,所以我们可以将所以同一个叶子结点的样本重组起来,过程如下:
因此通过上式的改写,我们可以将目标函数改写成关于叶子结点分数 的一个一元二次函数,求解最优的和目标函数值就变得很简单了。
对于一个固定的结构 ,我们可以计算叶节点
的最优权重
:
并且计算对应的最优损失函数:
因此,最优的 和目标函数公式为:
分裂结点算法在上面的推导中,我们知道了如果我们一棵树的结构确定了,如何求得每个叶子结点的分数。但我们还没介绍如何确定树结构,即每次特征分裂怎么寻找最佳特征,怎么寻找最佳分裂点。
在CART一节提到过,基于空间切分去构造一颗决策树是一个NP难问题,我们不可能去遍历所有树结构,因此,XGBoost使用了和CART回归树一样的想法,利用贪心算法,遍历所有特征的所有特征划分点,不同的是使用上式目标函数值作为评价函数。具体做法就是分裂后的目标函数值比单子叶子节点的目标函数的增益,同时为了限制树生长过深,还加了个阈值,只有当增益大于该阈值才进行分裂。
假设 和
是拆分后左右节点的实例集,则
。拆分之后的损失减少为:
这个公式通常被用于评估分割候选集(选择最优分割点),其中前两项分别是切分后左右子树的的分支之和,第三项是未切分前该父节点的分数值,最后一项是引入额外的叶节点导致的复杂度。同时可以设置树的最大深度、当样本权重和小于设定阈值时停止生长去防止过拟合。
正则化
XGBoost的正则化项为: ,注意:这里出现了
和
,这是XGBoost自己定义的,在使用XGBoost时,你可以设定它们的值,显然,越大,表示越希望获得结构简单的树,因为此时对较多叶子节点的树的惩罚越大。越大也是越希望获得结构简单的树。
对缺失值处理
当样本的第 个特征值缺失时,无法利用该特征进行划分时,XGBoost的想法是将该样本分别划分到左结点和右结点,然后计算其增益,哪个大就划分到哪边。

XGBoost的优缺点
XGBoost可以成为机器学习的大杀器,广泛用于数据科学竞赛和工业界,是因为它有许多优点:
- 使用许多策略去防止过拟合,如:正则化项、Shrinkage and Column Subsampling等。
- 目标函数优化利用了损失函数关于待求函数的二阶导数。
- 支持并行化,这是XGBoost的闪光点,虽然树与树之间是串行关系,但是同层级节点可并行。具体的对于某个节点,节点内选择最佳分裂点,候选分裂点计算增益用多线程并行。训练速度快。
- 添加了对稀疏数据的处理。
- 交叉验证,early stop,当预测结果已经很好的时候可以提前停止建树,加快训练速度。
- 支持设置样本权重,该权重体现在一阶导数
和二阶导数
,通过调整权重可以去更加关注一些样本。
但是也存在缺点:
- 算法采用贪心策略,较为耗时。
应用场景
常用的分类问题的场景都可以引入XGBoost作为分类器,而且基本都是最优结果。在推荐领域中,我们常常把推荐问题映射成一个分类问题。通过收集用户的打分数据进行分析并推断出用户行为模型,进而对某个产品进行预测打分。一般情况下通过将物品属性和用户属性的各个特征作为输入,将打分作为类别转换为一个分类问题甚至是预测“next item”问题。这里面,输入数据假设为 的二元组,每个组内包括用户
的特征向量和物品
的特征向量,我们预测该用户是否点击了该物品,这样就将推荐问题转换为了分类问题。在业界,一般情况下处理这种分类问题有两种途径,一为LR+XGBoost,二为End-to-End模型;其中第一种因为部署简单,效果好而被广泛使用,但面临特征工程的问题,第二种模型设计部署非常复杂,但是效果往往会更优化一点。作为一般推荐系统而言,使用XGBoost作为推荐模型的基础算法或CTR预估问题的基础算法是一个比较合理的方式,关于这部分内容就不在赘述了,网上资料很多。




