决策树的优化-随机森林

重要内容简述：

     从ID3到C4.5再到CART 

     在分类树问题中（注意ID3和C4.5只能解决分类问题，CART是既可以解决分类问题，也可以解决回归问题）：最主要的是要进行分类的最优特征和最优切分点的选择，为了这两个量，算法不断的计算每一层的最优特征和对应下的最优切分点

    随机森林

    属于集成学习的范畴，在随机森林中，决策树模型作为一个基学习器，由于决策树就是根据已知的特征中进行最优特征和最优切分点的选择进行划分，随机森林能够将特征集合取样分为不同个子特征集合，这样每个特征集的最优特征和最优切分点不同，同时引起最终基决策树（基学习器）不同，最后通过组合策略，展示非常好的泛化能力，非常好的学习效果

    ID3的划分标准

     ID3是基于信息增益的，信息增益的计算公式如下

信息增益 = 原问题的信息熵 - 原问题的条件熵  

     信息增益计算时，前项是所有样本的信息熵，后项是假定划分属性下，得到的信息争议（前面有权重的计算），但是前后两项都是计算结果的信息熵（然后进行比较）

 

ID3 应用信息增益的问题

应用信息增益选择划分属性的时候，很明显有例如学号类似的属性  是优先的选择标准，但是这个选择标准是没有很大意义的划分

C4.5的选取划分属性的标准 信息增益率公式如下：

 信息增益率的理解

     由于信息增益存在的问题，引入信息增益率，信息增益率加入了分母计算的   单独属性的信息熵，   这个信息上犹如计算结果的信息熵一样，显然，类似学号这样的属性的具有很大的信息熵，（学号的属性有很多取值，可以看到每一个样本取一个值，信息熵最大），为了避免这种无意义属性的选择加入此分母，能够权衡在选择相对好的属性的情况下提高尽可能高的信息增益

   CART 是区别于 ID3 和 C4.5 CART划分得到二叉树

  划分标准就是基尼指数

基尼指数和信息增益的区别和联系

     对信息增益的  -log P 进行一阶泰勒展开得到 (1 - P) 在忽略泰勒展开的高阶无穷小的情况

所以 基尼指数是约等于信息增益的

 

决策树与回归树

决策树与回归树的思想一样，需要找到最优切分属性和切分点

回归树是可以用于回归的决策树模型，一个回归树对应着输入空间的一个划分以及在划分单元上的输出值.与分类树不同的是，回归树对输入空间的划分采用一种启发式的方法，会遍历所有输入变量，找到最优的切分变量j和最优的切分点s，即选择第j个特征xj和它的取值s将输入空间划分为两部分，然后重复这个操作。 
而如何找到最优的j和s是通过比较不同的划分的误差来得到的。一个输入空间的划分的误差是用真实值和划分区域的预测值的均方差值的和来衡量的

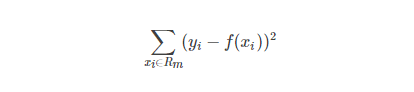
其中，f(xi)是每个划分单元的预测值，这个预测值是该单元内每个样本点的值的均值

 

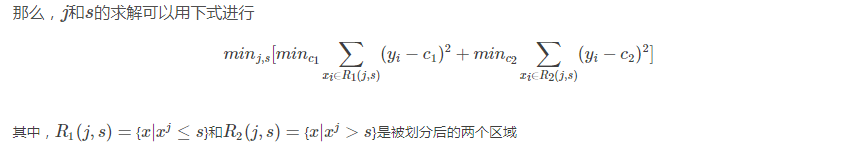
 正则化描述：

从决策树到随机森林

  Bagging思想：训练多个模型的融合的思想

集成的时候通过集成方法例如：分类应用投票机制

                                                  回归应用求平均值

Random Forest(随机森林)是一种基于树模型的Bagging的优化版本

1.对训练的样本进行有放回取样

2.对样本的属性进行有放回取样

问题：

一、熵和信息增益怎么理解，信息增益率提出的原因

二、正则化的极大似然函数和NP问题怎么理解

三、信息熵增益和基尼指数   都是为了表现 数据集在某个特征介入后 不确定性 变化的衡量指数，为什么还要选两个不同的划分准则

四、分类误差率怎么表示

五、ID3算法中最优切分点怎么计算的（怎么就忽略了），ID3算法中的阀值ε是什么作用

六、CART决策树中反复提到一个概念"二叉树",二叉树和CART有什么样的关系

思路：

一、熵和信息增益是度量样本集合的混乱程度的，作为度量属性是否是相对最优的标准

二、还没有解决

三、信息熵增益和基尼指数都是作为最先划分特征和最有切分点之争的选择准则：基尼指数求出后，可以直接对比得到相对最优特征和最优特征对应下最优切分点；信息熵增益

       可以看到在对数据进行分析时会时不时提到特征A，B，C，D等，此时是在数据的给出特征进行分析，实际问题中需要做特征的单独提取，即特征工程

      CAR回归树在《统计学习方法》中提到的比较少，CART是二叉树，不同于ID3或者C4.5都是可以进行多个叉分类