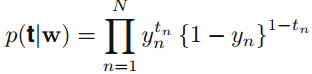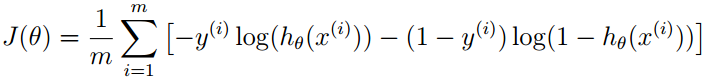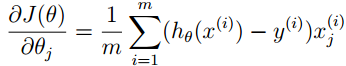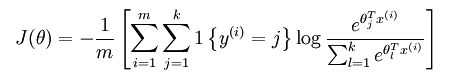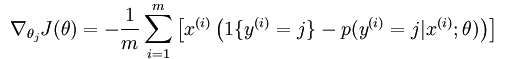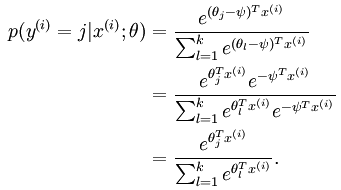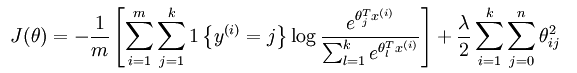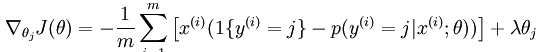Logistic and Softmax Regression (逻辑回归和Softmax回归)
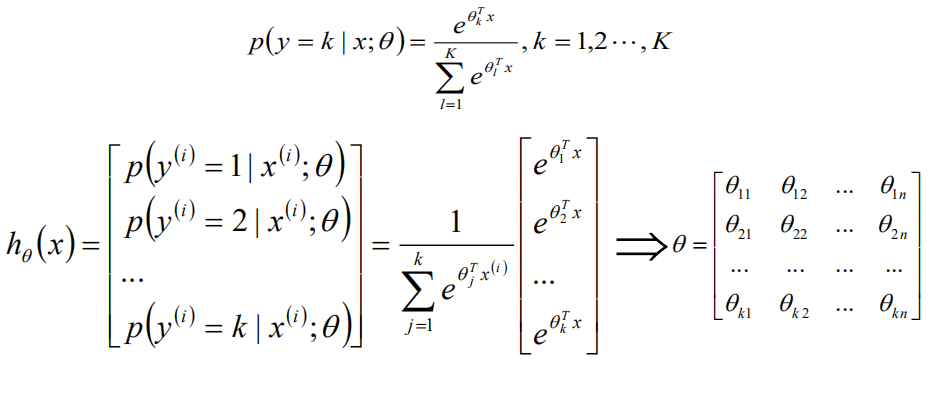
1． 简介
逻辑回归和Softmax回归是两个基础的分类模型，虽然听名字以为是回归模型，但实际我觉得他们也有一定的关系。逻辑回归，Softmax回归以及线性回归都是基于线性模型，它们固定的非线性的基函数（basis function）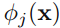
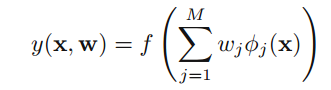
其中，如果f（.）是非线性的激活函数（activation function），这就是一个分类模型；如果f（.）是恒等函数（identity），则是回归模型，现在可以发现它们三者的联系了吧。
下面主要谈谈逻辑回归，Softmax回归，前者主要处理二分类问题，而后者处理多分类问题，但事实上Softmax回归就是逻辑回归的一般形式。
2． 逻辑回归
定义逻辑回归hypothesis为
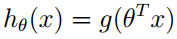
其中，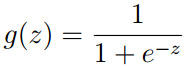
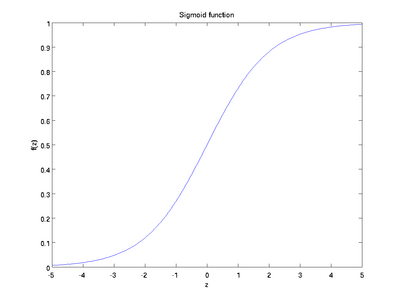
逻辑回归的理激活函数是sigmoid函数，可理解成一个被sigmoid函数归一化后的线性回归。因为sigmoid函数把实数映射到了[0,1]区间，可以认为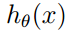
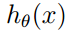
这里的y_n就是上面的 （由于参考了多本书，所以符号有一定的区别），一般会使用最大释然求解参数，这时取一个负的log对数（negative logarithm），得到：
上式被称为交叉熵(cross entropy) loss函数，因为取了一个负对数，之前的最大化就变成了最小化，所以只需求解是交叉熵loss函数最小的参数。
对loss函数求导得到：
到现在为止，我们已经得到了loss函数以及关于参数的偏导数，只需要通过梯度下降就可以得到参数的解，OK，大功告成。
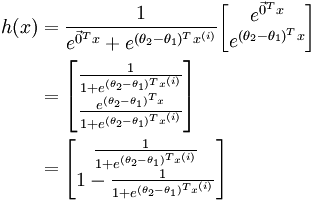
如果需要预测一个为止数据x，属于那个类，只需要带入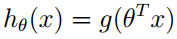
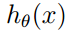
3． Softmax回归
Softmax回归处理多分类问题，我们假设函数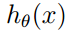 形式如下： 
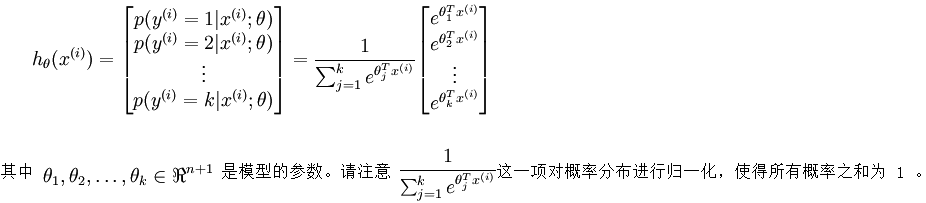
和逻辑回归一样，得到loss函数为：
其中的1{.}是一个指示性函数，即当大括号中的值为真时，该函数的结果就为1，否则其结果就为0。
然后计算损失函数的偏导函数，得到：
之后就可以用如果要用梯度下降法，或者L-BFGS法求得未知参数。
看上面的推到我们可以发现，对每一个参数减去一个参数，最后的结果没有影响。其实softmax 回归中对参数的最优化解不只一个，每当求得一个优化参数时，如果将这个参数的每一项都减掉同一个数，其得到的损失函数值也是一样的，这说明解不是唯一的。
之所以会出现这样的现象，因为损失函数不是严格非凸的，也就是说在局部最小值点附近是一个”平坦”的，所以在这个参数附近的值都是一样的了。
为避免出现这样的情况，加入正则项（比如说，用牛顿法求解时，hession矩阵如果没有加入规则项，就有可能不是可逆的从而导致了刚才的情况，如果加入了规则项后该hession矩阵就不会不可逆了），加入正则项后的loss函数表达式为：
此时loss函数的偏导函数为：
同样的，我们在逻辑回归中，也可以加上正则项。
4． 逻辑回归与Softmax回归的联系
我们在刚开始的时候说softmax 回归是逻辑回归的一般形式，现在我们看看两者之间的联系。当类别数k = 2 时，softmax 回归退化为逻辑回归，softmax 回归的假设函数为：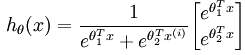
利用softmax回归参数冗余的特点，我们令
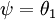，并且从两个参数向量中都减去向量 
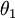，得到:
因此，用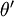
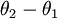
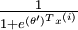
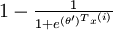
5． 与神经网络的关系
神经网络是一个多层次的分类模型，其实logistic回归和softmax回归可以看出最简单的神经网络，结构如下图所示：
一般的神经网络有输入层，隐含层以及输出层构成，而上图中只有输入层和输出层，而没有隐含层。神经网络处理二分类时，输出层为一个节点，但处理K（K>2）分类问题时，数据节点为K个，这个logistic回归和softmax回归保持一致。值得注意的，在神经网络中的最后一层隐含层和输出层就可以看成是logistic回归或softmax回归模型，之前的层只是从原始输入数据从学习特征，然后把学习得到的特征交给logistic回归或softmax回归处理。
因此，可以把处理分类问题的神经网络分成两部分，特征学习和logistic回归或softmax回归。
