数学基础 - 二项分布

 现在要开始讲到分布了，当然首先要谈的肯定是二项分布，在此之前，让我们先认识一下我们的前辈。

瑞士数学家雅克·伯努利(Jacques Bernoulli,1654～1705)首次研究独立重复试验(每次成功率为p)。在他去世后的第8年(1713年)，他侄子尼克拉斯出版了伯努利的著作《推测术》。在书中，伯努利指出了如果这样的试验次数足够大，那么成功次数所占的比例以概率1接近p。 雅克·伯努利是这个最著名的数学家庭的第一代。在后来的三代里，一共有8到12个伯努利，在概率论、统计学和数学上做出了杰出的基础性贡献。

 

伯努利分布 在一次试验中，事件A出现的概率为p，不出现的概率为q=1-p。若以β记事件A出现的次数，则β仅取0，1两值，相应的概率分布为：

二项分布是指在只有两个结果的n次独立的伯努利试验中，所期望的结果出现次数的概率。在单次试验中，结果A出现的概率为p，结果B出现的概率为q，p+q=1。那么在n=10，即10次试验中，结果A出现0次、1次、……、10次的概率各是多少呢？这样的概率分布呈现出什么特征呢？这就是二项分布所研究的内容。

还是先举个例子吧。

掷一枚硬币(怎么老是硬币？小学的时候就讲了)出现正面和反面的概率各为0.5，那么掷1次，出现正面的概率肯定是0.5。掷2次、掷3次呢？

掷2次出现的结果有4个，正正、正反、反正、反反。因为p=0.5，所以每个结果出现的概率是0.5×0.5=0.25，那正面出现2次、1次、0次的概率分别是0.25、0.5、0.25。

掷3次出现的结果有8个，正正正、正正反、正反正、正反反、反正正、反正反、反反正、反反反。每个结果出现的概率是0.5×0.5×0.5=0.125，那正面出现3次、2次、1次、0次的概率分别是0.125、0.375、0.375、0.125。

统计学家们总结出了计算概率的一般公式

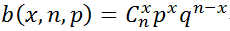
其中b表示二项分布的概率，n表示试验次数，x表示出现某个结果的次数。是组合，表示在n次试验中出现x次结果的可能的次数。如10次试验，出现0次正面的次数有1次，出现1次正面的次数有10次，……，出现5次正面的次数有252次，等等。其计算也有一个通式：

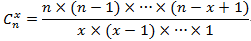
也可以写成：

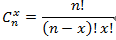
如果这个公式你算不好，就查下面的杨辉三角形吧，每一行的数字是上一行相邻两个数字的和。在下图中，每一行表达的是展开式的各项系数，下图列出了n=0,1,…,16时展开式中各项的系数。

需要特别提醒的是：二项分布是建立在有放回抽样的基础上的，也就是抽出一个样品测量或处理完后再放回去，然后抽下一个。在实际的工作中通常我们很少会这样抽，一般都属于无放回抽样，这时候需要用超几何分布来计算概率。在一般的教课书上都会要求，当总体的容量N不大时，要用超几何分布来计算，如果N很大而n很小，则可以用二项分布来近似计算，也就是可以将无放回抽样近似看出有放回抽样。至于n要小到什么程度，有的书上说n/N小于0.1就可以了，有的书上则要求小于0.05。

上面讲得有点干，下面举个例子。

在很多工厂里，通常都会跟零件供应商约定供货合格率，并对每批供货进行抽检，就是所谓的IQC。设约定的合格品率为97%，如果每批随机抽10件，那么抽出1件不合格时，整批的零件的合格率是不是达不到97%？

根据题意，p=0.97，n=10，x=9，据此算出10个样品中有9个合格品的概率是

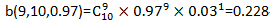
反过来，如果考虑不合格品率，p=0.03，n=10，x= 1，据此计算出10个样品中有1个不合格品的概率是

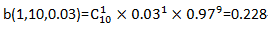
结果是一样的。由此可见，10个样品中有1个不合格品的概率还是很大的，因此不能说这批零件不合格。

那抽出2个不合格的呢？同样可以算出

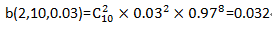
概率非常小，而且抽出超过2个以上不合格品的概率会更小，因此如果10个样品中有2个或以上的不合格品，则整批的零件合格率肯定达不到97%，可以整批退货。

如果约定的合格率是99.5%，则出现0个、1个、2个不合格品的概率分别为0.951、0.0478、0.001，如此10个只要抽出1个不合格品就可以整批退货了。

有人会问，到底应该抽多少样呢？这在GB/T2828里有明确规定，限于篇幅，这里只介绍其中一种最简单的应用原理，具体应用时大家可以去查国标。

假设你与供应商约定的接收合格率是99%，即AQL(接收质量限)=0.01，本批的总数量是1000只，只做一般性的检验，查国标可得抽样量为80；Ac=2，即抽到2个及以下不合格品可接收该批；Re=3，即抽到3个及以上不合格品则拒绝接收。

限于人力物力，你可能无法抽这么多的样，根据该供应商以往的表现，你制定了两种抽样方案，一种是抽20个，不合格品为0接收，大于0退回；另一种是抽50个，不合格品不超过1则接收，大于1则退回。我们来看看，如果这批来料合格率只有98%，按照这两种抽样方案以及国标的方案，你接收的概率有多大。为了方便我们用Excel来算。

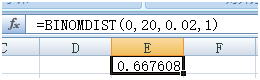
方案一

 

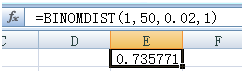
方案二

 

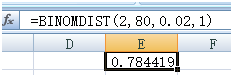
国标方案

这几种方案接收的概率都不小，这就是抽样检验带来的风险。如果实际批合格率低于约定合格率，仍被接收的风险属于使用者风险。

反过来，如果批合格率高于约定合格率，如99.5%，那有多大的可能性拒绝该批呢？我们也可以用二项分布来计算。

我们可以看到，即使实际合格率高于约定，仍然存在拒收的风险，虽然这个风险并不大，通常这一类的风险叫做生产者风险。

根据不同的批合格率，可以计算出每一种抽样方案的两类风险，画出OC曲线。用方案一画出的OC曲线如下：

 

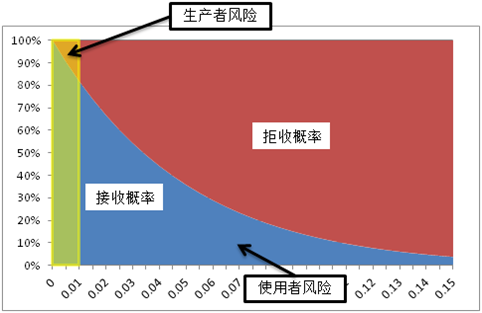
图中横坐标为实际的批不合格率，纵坐标为接收概率，曲线下方为接收概率，上方为拒收概率，可以看出即使来料不合格率远高于约定，接收的概率还是很大的。黄色的矩形框称为理想曲线，理想的情况下，批不合格率低于约定肯定接收，而超过约定则肯定拒收，但这种理想曲线是不可能达到的，只能尽可能接近。

下面我们再看看三种抽样方案的OC曲线之间的对比。

 

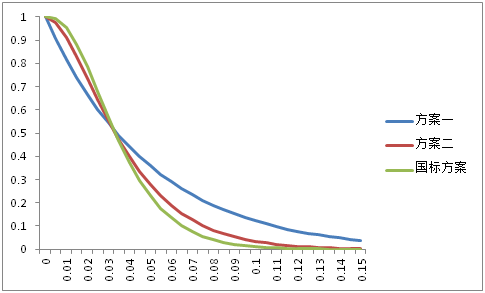
三种方案各有优劣势，但国标方案的下降趋势要比另外两种要快，更接近理想曲线。当然你也可以试一下其它的抽样方案，有可能会找到更好的。

确定抽样方案不是靠拍脑袋来决定的，需要对抽样方案进行比较深入的研究，找到最恰当的抽样方案。

另外，关于抽样问题要具体问题具体分析，如果供应商质量控制能力很强，可以放宽检验甚至免检(可以将此作为供应商的激励措施，这也是我在客户那里极力推动的，虽然这项政策最终是依据国内一个质量大腕的建议制定的，我仍然觉得非常高兴)；如果供应商质量控制能力很差，就需要加严检验。有时要控制误检，有时要控制漏检，这要看成本与收益。我曾经服务的一家客户对一个零件专门配10个人进行全检，就是为了防止漏检，因为必须要100%合格，否则因为漏检造成客户的索赔是承受不起的。

本文所描述的仅仅是国标中最基本、最简单的应用，当遇到各种复杂的情况时，要想到去参考国标。

最后再说一下二项分布的正态近似。在大样本的情况下，二项分布的计算会很麻烦，这时可以采用正态分别来近似，其条件是np和n(1-p)都大于5。采用正态分布的参数为：