标准化与归一化的区别
很多人认为标准化理解为归一化，然而是有区别的，下面告诉你不同之处：
（一）归一化
特点
对不同特征维度的伸缩变换的目的是使各个特征维度对目标函数的影响权重是一致的，即使得那些扁平分布的数据伸缩变换成类圆形。这也就改变了原始数据的一个分布。
好处
1 提高迭代求解的收敛速度
2 提高迭代求解的精度
（二）标准化
特点
对不同特征维度的伸缩变换的目的是使得不同度量之间的特征具有可比性。同时不改变原始数据的分布。
好处
1 使得不同度量之间的特征具有可比性，对目标函数的影响体现在几何分布上，而不是数值上
2 不改变原始数据的分布
举例
根据人的身高和体重预测人的健康指数
假设有如下原始样本数据是四维的（当然一般不会有这么无聊的数据）
从上面两个坐标图可以看出，样本在数据值上的分布差距是不一样的，但是其几何距离是一致的。而标准化就是一种对样本数据在不同维度上进行一个伸缩变化（而不改变数据的几何距离），也就是不改变原始数据的信息（分布）。这样的好处就是在进行特征提取时，忽略掉不同特征之间的一个度量，而保留样本在各个维度上的信息（分布）。
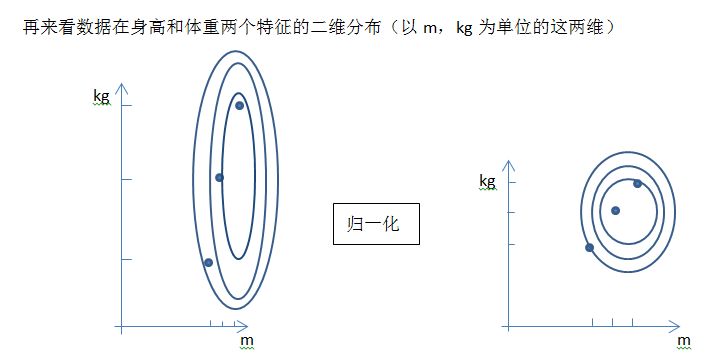
从采用大单位的身高和体重这两个特征来看，如果采用标准化，不改变样本在这两个维度上的分布，则左图还是会保持二维分布的一个扁平性；而采用归一化则会在不同维度上对数据进行不同的伸缩变化（归一区间，会改变数据的原始距离，分布，信息），使得其呈类圆形。虽然这样样本会失去原始的信息，但这防止了归一化前直接对原始数据进行梯度下降类似的优化算法时最终解被数值大的特征所主导。归一化之后，各个特征对目标函数的影响权重是一致的。这样的好处是在提高迭代求解的精度。
