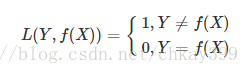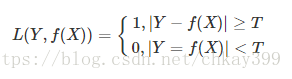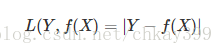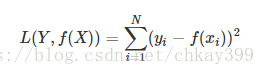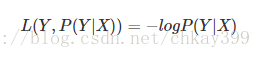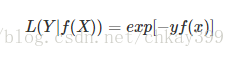机器学习 - 损失函数总结

 

 

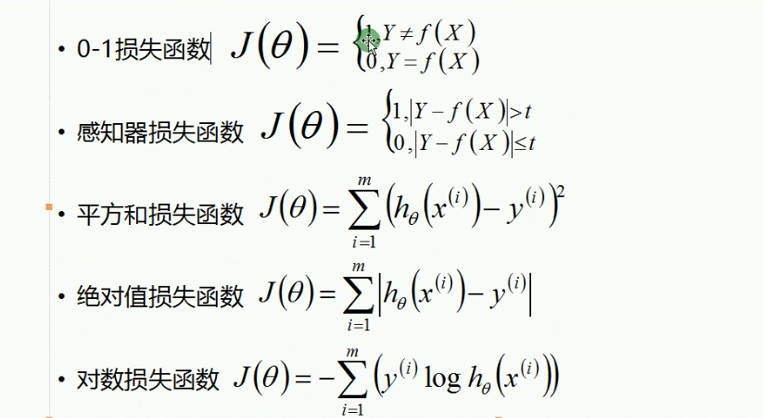
经典机器学习算法，他们最本质的区别是分类思想（预测y的表达式）不同，有的是基于概率模型，有的是动态规划，表象的区别就是最后的损失函数不同。

损失函数分为经验风险损失函数和结构风险损失函数，经验风险损失函数反映的是预测结果和实际结果之间的差别，结构风险损失函数则是经验风险损失函数加上正则项(L0、L1（Lasso）、L2（Ridge）)。

不同的算法常用的损失函数（Loss Function）有：

一、0-1损失函数（gold standard 标准式）

       0-1损失是指，预测值和目标值不相等为1，否则为0： 

                                                   

      该损失函数不考虑预测值和真实值的误差程度，也就是说只要预测错误，预测错误差一点和差很多是一样的。感知机就是用的这种损失函数，但是由于相等这个条件太过严格，我们可以放宽条件，即满足 |Y−f(X)|<T时认为相等。 

                                                     

       这种损失函数用在实际场景中比较少，更多的是用俩衡量其他损失函数的效果。

二、绝对值损失函数

        绝对值损失函数，（暂时还不知道用在啥场合，了解后改正）：

                                               

三、平方损失函数（squared loss）

       实际结果和观测结果之间差距的平方和，一般用在线性回归中，可以理解为最小二乘法：

                                                       

       

四、对数损失函数（logarithmic loss）

       主要在逻辑回归中使用，样本预测值和实际值的误差符合高斯分布，使用极大似然估计的方法，取对数得到损失函数：

                                                             

       损失函数L(Y,P(Y|X))L(Y,P(Y|X))是指样本X在分类Y的情况下，使概率P(Y|X)达到最大值。

       经典的对数损失函数包括entropy和softmax，一般在做分类问题的时候使用（而回归时多用绝对值损失（拉普拉斯分布时，μ值为中位数）和平方损失（高斯分布时，μ值为均值））。

 

五、指数损失函数（Exp-Loss）

       在boosting算法中比较常见，比如Adaboosting中，标准形式是：

                                                              

六、铰链损失函数（Hinge Loss）

       铰链损失函数主要用在SVM中，Hinge Loss的标准形式为：

                                                              

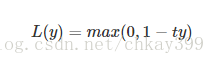
       y是预测值，在-1到+1之间，t为目标值（-1或+1）。其含义为，y的值在-1和+1之间就可以了，并不鼓励|y|>1|y|>1，即并不鼓励分类器过度自信，让某个正确分类的样本的距离分割线超过1并不会有任何奖励，从而使分类器可以更专注于整体的分类误差。