密码库LibTomcrypt的内容介绍及分析
密码库LibTomcrypt的内容介绍及分析
2.1 密码知识简介
2.1.1专业术语
发送者和接收者
假设发送者想发送消息给接收者,且想安全地发送信息:她想确信偷听者不能阅读发送的消息。
2.1.2消息和加密
消息被称为明文。用某种方法伪装消息以隐藏它的内容的过程称为加密,加了密的消息称为密文,而把密文转变为明文的过程称为解密。图1.1表明了这个过程。
(如果你遵循ISO 7498-2标准,那就用到术语“译成密码(encipher)”和“解译密码(decipher)”。某些文化似乎认为术语“加密(encrypt)”和“解密(decrypt)”令人生厌,如同陈年腐尸。)
 图1.1 加密和解密
图1.1 加密和解密
使消息保密的技术和科学叫做密码编码学,从事此行的叫密码编码者,密码分析者是从事密码分析的专业人员,密码分析学就是破译密文的科学和技术,即揭穿伪装。作为数学的一个分支的密码学包括密码编码学和密码分析学两者,精于此道的人称为密码学家,现代的密码学家通常也是理论数学家。
明文用M(消息)或P(明文)表示,它可能是比特流(文本文件、位图、数字化的语音流或数字化的视频图像)。至于涉及到计算机,P是简单地二进制数据(除了这一章节外,这本书本身只涉及二进制数据和计算机密码学)。明文可被传送或存储,无论在哪种情况,M指待加密的消息。
密文用C表示,它也是二进制数据,有时和M一样大,有时稍大(通过压缩和加密的结合,C有可能比P小些。然而,单单加密通常达不到这一点)。加密函数E作用于M得到密文C,用数学表示为:
E(M)=C.
相反地,解密函数D作用于C产生M
D(C)=M.
先加密后再解密消息,原始的明文将恢复出来,下面的等式必须成立:
D(E(M))=M
2.1.3鉴别、完整性和抗抵赖
除了提供机密性外,密码学通常有其它的作用:.
-鉴别
消息的接收者应该能够确认消息的来源;入侵者不可能伪装成他人。
-完整性
消息的接收者应该能够验证在传送过程中消息没有被修改;入侵者不可能用假消息代替合法消息。
-抗抵赖
发送者事后不可能虚假地否认他发送的消息。
这些功能是通过计算机进行社会交流,至关重要的需求,就象面对面交流一样。某人是否就是他说的人;某人的身份证明文件(驾驶执照、医学学历或者护照)是否有效;声称从某人那里来的文件是否确实从那个人那里来的;这些事情都是通过鉴别、完整性和抗抵赖来实现的。
2.1.4算法和密钥
密码算法也叫密码,是用于加密和解密的数学函数。(通常情况下,有两个相关的函数:一个用作加密,另一个用作解密)
如果算法的保密性是基于保持算法的秘密,这种算法称为受限制的算法。受限制的算法具有历史意义,但按现在的标准,它们的保密性已远远不够。大的或经常变换的用户组织不能使用它们,因为每有一个用户离开这个组织,其它的用户就必须改换另外不同的算法。如果有人无意暴露了这个秘密,所有人都必须改变他们的算法。
更糟的是,受限制的密码算法不可能进行质量控制或标准化。每个用户组织必须有他们自己的唯一算法。这样的组织不可能采用流行的硬件或软件产品。但窃听者却可以买到这些流行产品并学习算法,于是用户不得不自己编写算法并予以实现,如果这个组织中没有好的密码学家,那么他们就无法知道他们是否拥有安全的算法。
尽管有这些主要缺陷,受限制的算法对低密级的应用来说还是很流行的,用户或者没有认识到或者不在乎他们系统中内在的问题。
现代密码学用密钥解决了这个问题,密钥用K表示。K可以是很多数值里的任意值。密钥K的可能值的范围叫做密钥空间。加密和解密运算都使用这个密钥(即运算都依赖于密钥,并用K作为下标表示),这样,加/解密函数现在变成:
EK(M)=C
DK(C)=M.
这些函数具有下面的特性(见图1.2):
DK(EK(M))=M.
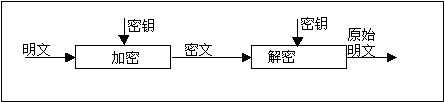
图1.2 使用一个密钥的加/解密
 图1.3 使用两个密钥的加/解密
图1.3 使用两个密钥的加/解密
有些算法使用不同的加密密钥和解密密钥(见图1.3),也就是说加密密钥K1与相应的解密密钥K2不同,在这种情况下:
EK1(M)=C
DK2(C)=M
DK2 (EK1(M))=M
所有这些算法的安全性都基于密钥的安全性;而不是基于算法的细节的安全性。这就意味着算法可以公开,也可以被分析,可以大量生产使用算法的产品,即使偷听者知道你的算法也没有关系;如果他不知道你使用的具体密钥,他就不可能阅读你的消息。
密码系统由算法、以及所有可能的明文、密文和密钥组成的。
2.1.5对称算法
对称密码算法有时又叫传统密码算法,就是加密密钥能够从解密密钥中推算出来,反过来也成立。在大多数对称算法中,加密解密密钥是相同的。这些算法也叫秘密密钥算法或单密钥算法,它要求发送者和接收者在安全通信之前,商定一个密钥。对称算法的安全性依赖于密钥,泄漏密钥就意味着任何人都能对消息进行加密解密。只要通信需要保密,密钥就必须保密。对称算法的加密和解密表示为:
Ek(M)=C
Dk(C)=M
对称算法可分为两类[8]。一次只对明文中的单个位(有时对字节)运算的算法称为序列算法或序列密码。另一类算法是对明文的一组位进行运算,这些位组称为分组,相应的算法称为分组算法或分组密码。现代计算机密码算法的典型分组长度为64位――这个长度大到足以防止分析破译,但又小到足以方便作用。
这种算法具有如下的特性:
Dk(Ek(M))=M
常用的采用对称密码术的加密方案有5个组成部分
l)明文:原始信息。
2)加密算法:以密钥为参数,对明文进行多种置换和转换的规则和步骤,变换结果为密文。
3)密钥:加密与解密算法的参数,直接影响对明文进行变换的结果。
4)密文:对明文进行变换的结果。
5)解密算法:加密算法的逆变换,以密文为输入、密钥为参数,变换结果为明文。
对称密码术的优点在于效率高(加/解密速度能达到数十兆/秒或更多),算法简单,系统开销小,适合加密大量数据。
尽管对称密码术有一些很好的特性,但它也存在着明显的缺陷,包括:
l)迸行安全通信前需要以安全方式进行密钥交换。这一步骤,在某种情况下是可行的,但在某些情况下会非常困难,甚至无法实现。
2)规模复杂。举例来说,A与B两人之间的密钥必须不同于A和C两人之间的密钥,否则给B的消息的安全性就会受到威胁。在有1000个用户的团体中,A需要保持至少999个密钥(更确切的说是1000个,如果她需要留一个密钥给他自己加密数据)。对于该团体中的其它用户,此种倩况同样存在。这样,这个团体一共需要将近50万个不同的密钥!推而广之,n个用户的团体需要N2/2个不同的密钥。
通过应用基于对称密码的中心服务结构,上述问题有所缓解。在这个体系中,团体中的任何一个用户与中心服务器(通常称作密钥分配中心)共享一个密钥。因而,需要存储的密钥数量基本上和团体的人数差不多,而且中心服务器也可以为以前互相不认识的用户充当“介绍人”。但是,这个与安全密切相关的中心服务器必须随时都是在线的,因为只要服务器一掉线,用户间的通信将不可能进行。这就意味着中心服务器是整个通信成败的关键和受攻击的焦点,也意味着它还是一个庞大组织通信服务的“瓶颈”
2.1.6公开密钥算法
公开密钥算法(也叫非对称算法)是这样设计的:用作加密的密钥不同于用作解密的密钥,而且解密密钥不能根据加密密钥计算出来(至少在合理假定的长时间内)。之所以叫做公开密钥算法,是因为加密密钥能够公开,即陌生者能用加密密钥加密信息,但只有用相应的解密密钥才能解密信息。在这些系统中,加密密钥叫做公开密钥(简称公钥),解密密钥叫做私人密钥(简称私钥)。私人密钥有时也叫秘密密钥。为了避免与对称算法混淆,此处不用秘密密钥这个名字。
用公开密钥K加密表示为
EK(M)=C.
虽然公开密钥和私人密钥是不同的,但用相应的私人密钥解密可表示为:
DK(C)=M
有时消息用私人密钥加密而用公开密钥解密,这用于数字签名(见2.6节),尽管可能产生混淆,但这些运算可分别表示为:
EK(M)=C
DK(C)=M
2.2 LibTomCrypt密码库主要内容
2.2.1 1LibTomCrypt密码库主要包含以下内容:
1、 高级加密标准AES(Advanced Encryption Standard) Rijndael和AES候选算法:RC6, MARS, Twofish, Serpent, CAST-256。
1997年4月15日美国国家标准技术研究所NIST发起征集高级加密标准AES算法的活动,2001年11月26日,NIST正式公布Rijndael数据加密算法为高级加密标准AES, 经过多年来的分析和测试,至今没有发现AES的明显缺点,也没有找到明显的安全漏洞. AES能够抵抗目前已知的各种攻击方法。
2、 对称分组密码:IDEA, DES, Triple-DES (DES-EDE2 and DES-EDE3), DESX (DES-XEX3), RC2, RC5, Blowfish, Diamond2, TEA, SAFER, 3-WAY, GOST, SHARK, CAST-128, Square, Skipjack。
分组密码又称为秘密钥密码或对称密码。利用分组密码对明文进行加密时,首先需要对明文进行分组,每组的长度都相同,然后对每组明文分别加密得到等长的密文,分组密码的特点是加密密钥与解密密钥相同。分组密码的安全性应该主要依赖于密钥,而不依赖于对加密算法和解密算法的保密。
3、 一般的密码模式:电子密本(ECB),密码分组链接(CBC),输出反馈(OFB)和密文反馈(CFB)。
4、 序列密码:Panama, ARC4, SEAL, WAKE, WAKE-OFB, BlumBlumShub 。
序列密码可以认为是起源于20世纪20年代的Vernam体系,当Vernam体制中的密钥序列是随机的(0,1)时,就是所谓“一次一密“密码体制。Shannon已经证明了“一次一密“密码体制在理论上是不可破译的。在序列密码中,加密和解密所用的密钥都是伪随机序列,伪随机序列的产生比较容易并且有比较成熟的数学理论工具,目前,序列密码是 世界各国的军事和外交等领域中使用的主要密码体制之一。
5、 公钥密码: RSA, DSA, ElGamal, Nyberg-Rueppel (NR), Rabin, Rabin-Williams (RW), LUC, LUCELG, DLIES (variants of DHAES), ESIGN。
6、在公钥密码体制中加秘密钥和解密密钥是不一样的,加密密钥可以公开传播而不危及密码体制的安全性。RSA公钥密码体制的安全性是基于大整数的素分解问题的难解性,ElGamal公钥密码体制的安全性是基于有限域上的离散对数问题上的难解性,而Menezes Vanstone公钥密码体制的安全性则是基于椭圆曲线上的离散对数问题的难解性。
7、公钥密码系统补丁:PKCS#1 v2.0, OAEP, PSSR, IEEE P1363 EMSA2 。
8、 密钥协商协议(key agreement schemes):Diffie-Hellman (DH), Unified Diffie-Hellman (DH2), Menezes-Qu-Vanstone (MQV), LUCDIF, XTR-DH 。
密钥协商是一种协议,利用这种协议,通讯双方可以在一个公开的信道上通过相互传送一些消息来共同建立一个共享的秘密密钥。在密钥协商中,双方共同建立的秘密密钥通常是双方输入消息的一个函数。
9、椭圆曲线密码:ECDSA, ECNR, ECIES, ECDH, ECMQV。
10、单向hash函数:SHA-1:安全hash算法SHA,MD2, MD4, MD5, HAVAL, RIPEMD-160, Tiger, SHA-2 (SHA-256, SHA-384, and SHA-512), Panama。
Hash函数是一种将一种任意长度的消息(message)压缩为某一固定长度的消息摘要(message digest)的函数。Hash函数可以用于数字签名和消息的完整性检测。Hash函数 MD4是由R.L.Rivest于1990年提出的。MD4的设计没有基于任何假设和密码体制。Hash函数的这种直接构造方法受到人们的广泛青睐。MD4的效率很高,非常实用。关于MD4的安全性目前还没发现非常有效的攻击方法,但是已经有人指出它的一些不足,为了克服MD4的缺陷和增强安全性,R.L.Rivest于1991年对MD4作了改进,改进后的Hash函数称为MD5。SHA即安全Hash算法是美国国家标准技术研究所(NIST)公布的安全Hash标准(SHS)中的Hash算法,1995年NIST修改SHS后将修改后的SHA称为SHA-1。SHA的设计原则与MD4的设计原则极其相似,它是MD4的一种变形。
11、消息认证码(MAC):MD5-MAC, HMAC, XOR-MAC, CBC-MAC, DMAC。
消息认证代码(MAC)并不是密码,而是校验和(通常是 32 位)的一种特殊形式,它是通过使用一个秘钥并结合一个特定认证方案而生成的,并且附加在一条消息后。消息摘要是使用单向散列函数生成的,紧密联系的数字签名是使用非对称密钥对生成并进行验证的。与这两者相比,预期的接收 方需要对秘钥有访问权,以便验证代码。
基于分组密码CBC的工作模式和CFB的工作模式的Hash函数中的密钥可以公开也可以不公开,如果密钥保密则Hash函数称为带密钥Hash函数,带密钥的Hash函数常用于产生消息认证码(MAC)对于通信双方之间传输的任意消息message,用带密钥的Hash函数H对message做变换,结果H(message)作为消息message的认证码,附在消息message的后面。消息认证码用于保证通讯双方之间传输信息的完整性,使双方确信消息没有被第三方篡改或伪造。
12、基于密码结构的Hash函数:Luby-Rackoff, MDC。
13、伪随机数发生器(PRNG): ANSI X9.17 appendix C, PGP's RandPool。
14、基于密码的密钥来源函数(password based key derivation functions):采用公开密码匙加密标准 PKCS #5 的PBKDF1 和 PBKDF2。
15、压缩和解压算法。
16、大整数和多项式快速精确算法。
17、有限域算法,包括GF(p) 和 GF(2^n)。
18、大素数的产生和验证。
2.2.2 介绍
在本库中,应用程序接口(API)是非常容易记忆和应用的。很多函数返回Void或者
int类型。函数返回int类型时如果函数执行成功,会返回CRYPT_OK。有些函数返回int类型的整数-1,表明函数执行错误。当一个函数确实返回错误时,他会被下面的函数转换为一个字符串。
const char *error_to_string(int err);
void somefunc(void)
{
if ((err = some_crypto_function(...)) -->= CRYPT_OK) {
printf("A crypto error occured, %s"n", error_to_string(err));
/* 下面执行错误处理*/
。。。。。。
}
/* 如果没有错误继续执行 */
。。。。。。
}
为了在程序中加入LibTomCrypt库,只需要加入#include “tomcrypt.h"就可以了,如下所示:
#include <tomcrypt.h>
int main(void) {
return 0;
}
这个头文件” tomcrypt.h”,包括”stdio.h”,”string.h", “stdlib.h",”time.h", “ctype.h" 和”ltc_ tommath.h"
(大整数库的程序)
2.2.3 宏定义
有些帮助的宏定义会使得代码简单些
宏定义如下:
STORE32L(x, y) unsigned long x, unsigned char *y x --> y[0 : : : 3]
STORE64L(x, y) unsigned long long x, unsigned char *y x --> y[0 : : : 7]
LOAD32L(x, y) unsigned long x, unsigned char *y y[0 : : : 3] --> x
LOAD64L(x, y) unsigned long long x, unsigned char *y y[0 : : : 7] --> x
STORE32H(x, y) unsigned long x, unsigned char *y x --> y[3 : : : 0]
STORE64H(x, y) unsigned long long x, unsigned char *y x --> y[7 : : : 0]
LOAD32H(x, y) unsigned long x, unsigned char *y y[3 : : : 0] --> x
LOAD64H(x, y) unsigned long long x, unsigned char *y y[7 : : : 0] --> x
BSWAP(x) unsigned long x Swaps the byte order of x.
ROL(x, y) unsigned long x, unsigned long y x << y; 0 _ y _ 31
ROLc(x, y) unsigned long x, const unsigned long y x << y; 0 _ y _ 31
ROR(x, y) unsigned long x, unsigned long y x >> y; 0 _ y _ 31
RORc(x, y) unsigned long x, const unsigned long y x >> y; 0 _ y _ 31
ROL64(x, y) unsigned long x, unsigned long y x << y; 0 _ y _ 63
ROL64c(x, y) unsigned long x, const unsigned long y x << y; 0 _ y _ 63
ROR64(x, y) unsigned long x, unsigned long y x >> y; 0 _ y _ 63
ROR64c(x, y) unsigned long x, const unsigned long y x >> y; 0 _ y _ 63
2.2.4 函数带有各种长度的输出
一些函数比如说rsa export(),带有变长度的输出。为了避免buffer溢出,输出的长度必须保存起来,比如说:
#include <tomcrypt.h>
int main(void) {
rsa_key key;
unsigned char buffer[1024];
unsigned long x;
int err;
/* ... 生成RSA密钥 */
。。。。。。
x = sizeof(buffer);//X保存缓冲区buffer的输出长度
if ((err = rsa_export(buffer, &x, PK_PUBLIC, &key)) != CRYPT_OK) {
printf("Export error: %s"n", error_to_string(err));
return -1;
}
/* 如果rsa_export()成功,那么x 将会得到输出的长度*/
printf("RSA exported key takes %d bytes"n", x);
/* ... 对缓冲区buffer做些处理 */
return 0;
}
在上面的函数中,如果RSA公钥长度超过1024字节,函数会返回一个错误,这个错误信号表明Buffer缓冲区溢出。如果函数执行成功就会将输出的长度保存到X里面,这样盗用程序就会知道用了多少个字节
2.3对称密码算法
2.3.1 核心函数
LibTomCrypt提供了一批ECB模式界面密码。首先你需要注意你永远也无法直接使用ECB模式加密数据,这一点很重要很重要。所以你应该用ECB函数产生一个链式的模式,或者用已经提供的一种链式模式。所有的的密码都被写成ECB界面。
所有的密码被保存在一个symmet_ric_key变量里。LibTomCrypt允许所有的密码有一个相同的模型存储这些密码
1.Setup函数
int XXX_setup(const unsigned char *key, int keylen, int rounds,symmetric_key *skey);
这个XXX_setup函数设置用什么密钥加密,密钥的长度,加密的轮数。如果函数返回成功
将会有一个预定的密钥,存储在skey里。
加密解密用ECB模式,有下面的两个函数:
2.encrypt函数
void XXX_ecb_encrypt(const unsigned char *pt, unsigned char *ct, symmetric_key *skey);
3. decrypt函数
void XXX_ecb_decrypt(const unsigned char *ct, unsigned char *pt, symmetric_key *skey);
encrypt函数pt是输入,ct是输出。Decrypt函数正好相反
4.test函数
int XXX_test(void);
如果密码匹配正确,这个函数将会返回一个CRYPT_OK。
5.Keysize函数
int XXX_keysize(int *keysize);
这个函数返回CRYPT_OK,如果这个密钥的长度是合意的。例如:
#include <tomcrypt.h>
int main(void)
{
int keysize, err;
/* 20字节的密钥长度Twofish接受吗? */
keysize = 20;
if ((err = twofish_keysize(&keysize)) != CRYPT_OK) {
printf("Error getting key size: %s"n", error_to_string(err));
return -1;
}
printf("Twofish suggested a key size of %d"n", keysize);
return 0;
}
2.3.2一个用ECB模式blowfish加密解密的例子
#include <tomcrypt.h>
int main(void)
{unsigned char pt[8], ct[8], key[8];
symmetric_key skey;
int err;
/* ... key is loaded appropriately in ``key'' ... */
/* ... load a block of plaintext in ``pt'' ... */
/* schedule the key */
1The size of which depends on which cipher you are using.
2pt stands for plaintext.
3ct stands for ciphertext.
4As published in their design papers.
if ((err = blowfish_setup(key, /* 密钥将被用到 */
8, /* 密钥是 8 bytes 长 */
0, /* 0 用默认的轮数 */
&skey) /* 预定的密钥*/
) != CRYPT_OK) {
printf("Setup error: %s"n", error_to_string(err));
return -1;
}
/* encrypt the block */
blowfish_ecb_encrypt(pt, /*加密 8-byte 数组 */
ct, /*储存加密数据 */
&skey); /* 先前预定的密码 */
/* decrypt the block */
blowfish_ecb_decrypt(ct, /*解密 8-byte 数组*/
pt, /*储存解密数据*/
&skey); /*先前预定的密码*/
/* 现在就解密出ct中的数据,将解密出的数据放到pt中 */
return 0;
}
2.3.3 算法描述
为了方便,库提供了密码算法的描述存放在数组cipher_descriptor里,描述如下:
struct _cipher_descriptor {
char *name;
unsigned char ID;
int min_key_length,
max_key_length,
block_length,
default_rounds;
int (*setup)(const unsigned char *key, int keylen, int num_rounds, symmetric_key *skey);
void (*ecb_encrypt)(const unsigned char *pt, unsigned char *ct, symmetric_key *skey);
void (*ecb_decrypt)(const unsigned char *ct, unsigned char *pt, symmetric_key *skey);
int (*test)(void);
int (*keysize)(int *keysize);
};
加密名称 描述名称 分块大小(byte) 密钥长度 加密轮数
Blow_sh blow_fish _desc 8 8 : : : 56 16
X-Tea xtea _desc 8 16 32
RC2 rc2 _desc 8 8 : : : 128 16
RC5-32/12/b rc5_desc 8 8 : : : 128 12 : : : 24
RC6-32/20/b rc6 _desc 16 8 : : : 128 20
SAFER+ saferp _desc 16 16, 24, 32 8, 12, 16
AES aes _desc 16 16, 24, 32 10, 12, 14
Two_fish two_fish_ desc 16 16, 24, 32 16
DES des_desc 8 7 16
3DES) des3_desc 8 21 16
CAST5 cast5_desc 8 5 : : : 16 12, 16
Noekeon noekeon_desc 16 16 16
Skipjack skipjack_desc 8 10 32
Anubis anubis_desc 16 16 : : : 40 12 : : : 18
Khazad khazad_desc 8 16 8
: : :表示从多少到多少
为了完成加/解密有如下的函数 int find_cipher(char *name),
2.3.4LibTomCrypt库的应用:
实现用LibTomCrypt库从文件中读出数据进行用对称算法的加密,将密文保存到一个文件里。然后用对称算法解密出密文保存到另一个文件里。
核心代码:
unsigned char plaintext[10000],ciphertext[10000];
//密钥
unsigned char tmpkey[512], key[MAXBLOCKSIZE], IV[MAXBLOCKSIZE];
//输入、输出
unsigned char inbuf[512]; /* i/o block size */
unsigned long outlen, y, ivsize, x, decrypt;
symmetric_CTR ctr;//在tomcrypt_cipher.h(237)中定义
int cipher_idx, hash_idx, ks;
char *infile, *outfile, *cipher
//注册加密方法
void register_algs(void)
{
//int x;
#ifdef RIJNDAEL
register_cipher (&aes_desc);
#endif
#ifdef BLOWFISH
register_cipher (&blowfish_desc);
#endif
#ifdef XTEA
register_cipher (&xtea_desc);
#endif
#ifdef RC5
register_cipher (&rc5_desc);
#endif
#ifdef RC6
register_cipher (&rc6_desc);
#endif
#ifdef SAFERP
register_cipher (&saferp_desc);
#endif
#ifdef TWOFISH
register_cipher (&twofish_desc);
#endif
#ifdef SAFER
register_cipher (&safer_k64_desc);
register_cipher (&safer_sk64_desc);
register_cipher (&safer_k128_desc);
register_cipher (&safer_sk128_desc);
#endif
#ifdef RC2
register_cipher (&rc2_desc);
#endif
#ifdef DES
register_cipher (&des_desc);
register_cipher (&des3_desc);
#endif
#ifdef CAST5
register_cipher (&cast5_desc);
#endif
#ifdef NOEKEON
register_cipher (&noekeon_desc);
#endif
#ifdef SKIPJACK
register_cipher (&skipjack_desc);
#endif
#ifdef KHAZAD
register_cipher (&khazad_desc);
#endif
#ifdef ANUBIS
register_cipher (&anubis_desc);
#endif
如果注册失败,则返回-1
if (register_hash(&sha256_desc) == -1) {
printf("Error registering SHA256"n");
exit(-1);
}
if (register_prng(&yarrow_desc) == -1) {
printf("Error registering yarrow PRNG"n");
exit(-1);
}
if (register_prng(&sprng_desc) == -1) {
printf("Error registering sprng PRNG"n");
exit(-1);
}
}
cipher_idx = find_cipher(cipher);
if (cipher_idx == -1) {
printf("Invalid cipher entered on command line."n");
exit(-1);
}
///** 无此函数:invalid keysize; Error hashing key: Invalid hash specified.
//函数find_hash在tomcrypt_hash.h中声明
hash_idx = find_hash("sha256");
if (hash_idx == -1) {
printf("SHA256 not found...?"n");
exit(-1);
}
如果找不到find_hash函数,则返回-1,将结果返还给hash_idx
//结构cipher_descriptor在tomcrypt_cipher.h中定义
//cipher descriptor table, last entry has "name == NULL" to mark the end of table
ivsize = cipher_descriptor[cipher_idx].block_length;
ks = hash_descriptor[hash_idx].hashsize;
//将hash_descriptor[hash_idx].hashsize中的密钥的长度传给ks
if (cipher_descriptor[cipher_idx].keysize(&ks) != CRYPT_OK) {
printf("Invalid keysize???"n");
exit(-1);
}
演示结果:
加密过程:
if(decrypt!=1){ /* encrypt */
/* Setup yarrow for random bytes for IV */
if ((errno = rng_make_prng(128, find_prng("yarrow"), &prng, NULL)) != CRYPT_OK) {
printf("Error setting up PRNG, %s"n", error_to_string(errno));
}
/* You can use rng_get_bytes on platforms that support it */
/* x = rng_get_bytes(IV,ivsize,NULL);*/
x = yarrow_read(IV,ivsize,&prng);
if (x != ivsize) {
printf("Error reading PRNG for IV required."n");
exit(-1);
}
if (fwrite(IV,1,ivsize,fdout) != ivsize) {
printf("Error writing IV to output."n");
exit(-1);
}
if ((errno = ctr_start(cipher_idx,IV,key,ks,0,&ctr)) != CRYPT_OK) {
printf("ctr_start error: %s"n",error_to_string(errno));
exit(-1);
}
do {
y = fread(inbuf,1,sizeof(inbuf),fdin);
if ((errno = ctr_encrypt(inbuf,ciphertext,y,&ctr)) != CRYPT_OK) {
printf("ctr_encrypt error: %s"n", error_to_string(errno));
exit(-1);
}
if (fwrite(ciphertext,1,y,fdout) != y) {
printf("Error writing to output."n");
exit(-1);
}
} while (y == sizeof(inbuf));
fclose(fdout);
fclose(fdin);
解密过程:
if (decrypt) {
/* Need to read in IV */
if (fread(IV,1,ivsize,fdin) != ivsize) {
printf("Error reading IV from input."n");
exit(-1);
}
if ((errno = ctr_start(cipher_idx,IV,key,ks,0,&ctr)) != CRYPT_OK) {
printf("ctr_start error: %s"n",error_to_string(errno));
exit(-1);
}
/* IV done */
do {
y = fread(inbuf,1,sizeof(inbuf),fdin);
if ((errno = ctr_decrypt(inbuf,plaintext,y,&ctr)) != CRYPT_OK) {
printf("ctr_decrypt error: %s"n", error_to_string(errno));
exit(-1);
}
if (fwrite(plaintext,1,y,fdout) != y) {
printf("Error writing to file."n");
exit(-1);
}
} while (y == sizeof(inbuf));
fclose(fdin);
fclose(fdout);
加密解密的结果:
2.4公开密钥算法
2.4.1 公开密钥
公开密钥算法使用不同的密钥进行加密和解密运算,并且解密密钥不能从加密密钥变换获得。公开密钥算法通常都非常慢,因此公开密钥算法很多时候被应用到加密一组由其他途径产生的密钥,并通过公众网路进行传送,然后接受方用私钥解密后,在以后的对称算法里应用此传送过来的密钥。
RSA(Rivest-Shamir-Adelman)是使用最多的公开密钥算法,能够被应用在加密和数字签名中。大家普遍接受当足够长的密钥被使用后,RSA是足够安全的(512比特是不安全的,768比特是中等安全的,1024比特足够保障一般的安全传输。) RSA的安全依赖于大整数因数分解的难度。因数分解的快速发展将导致RSA出现问题。不过,目前RSA是这个世界上最重要的公开密钥算法。RSA的专利权将在今年失效(2000年),并且将可以被自由使用。
Bruce Schneier有专门的论文讨论使用RSA密钥推荐的长度,按现状而言,512比特是不足够的,1024比特可以被认为是很安全的,如果使用2048比特,应该可以保障今后十年的安全。值得一提的是,RSA对于Chosen Plaintext attack非常脆弱,并且新近发展的Timing Attack能够用来破解很多RSA的具体实现。如果对RSA进行正确的应用,可以缔造一个很安全的系统,但是一定要注意避免上述这两类攻击。很多RSA的实现可以被自由获取,例如 PGP,SSH。
什么是公钥密码体制
公钥密码又称为双钥密码和非对称密码,是1976年由Diffie和Hellman在其“密码学新方向”一文中提出的,见划时代的文献:
W.Diffie and M.E.Hellman, New Directrions in Cryptography, IEEE Transaction on Information Theory, V.IT-22.No.6, Nov 1976, PP.644-654
单向陷门函数是满足下列条件的函数f:
(1)给定x,计算y=f(x)是容易的;
(2)给定y, 计算x使y=f(x)是困难的。
(所谓计算x=f-1(Y)困难是指计算上相当复杂,已无实际意义。)
3)存在δ,已知δ 时,对给定的任何y,若相应的x存在,则计算x使y=f(x)是容易的。
注:1*.仅满足(1)、(2)两条的称为单向函数;第(3)条称为陷门性,δ 称为陷门信息。
2*.当用陷门函数f作为加密函数时,可将f公开,这相当于公开加密密钥。此时加密密钥便称为公开钥,记为Pk。 f函数的设计者将δ 保密,用作解密密钥,此时δ 称为秘密钥匙,记为Sk。由于加密函数时公开的,任何人都可以将信息x加密成y=f(x),然后送给函数的设计者(当然可以通过不安全信道传送);由于设计者拥有Sk,他自然可以解出x=f-1(y)。 3*.单向陷门函数的第(2)条性质表明窃听者由截获的密文y=f(x)推测x是不可行的
2.4.2 RSA算法
在1976年,Diffie 和Hellman发表了一篇叫《密码学新动向》的文章,介绍了公匙加密的概念,给密码学的研究者带来了很大的轰动。论文的核心就是陷门单向函数:一个方向上的操作是容易的,但是如果不知道秘密的陷门,即使所有人都知道函数本身,从反方向计算是不现实的。在这里,公匙的扮演的角色和函数相同,仅被有限的一部分人知道的机关就是私匙。
两年后,也就是1978年由Rivest, Shamir 和Adleman提出了被称为RSA的公匙密码系统。RSA算法建立在对整数的分解的数学难题上的。私匙是由三个数(p,q,d)组成,其中p和q是两个素数(具有大致相同的大小),而d和(p-1)*(q-1)互质。公匙由两个数(n,e)组成,其中n=pq,而e是(p-1)(q-1)取d为模的倒数,例如:
ed = 1 mod(p-1)(q-1).
假如爱丽斯想用鲍勃的公匙(n,e)加密,传送一些文本。她首先会把明文转换成小于n的整数m,用鲍勃的公匙(n,e)加密处理:
c = me mod n,
然后把结果c送给鲍勃。在鲍勃的这边,他就会用他的私匙(p,q,d)进行解密处理:
cd mod n = med mod n = m.
对于RSA,单向的陷门函数是能够从一个小于n的整数x得到xe mod n.
RSA算法中用到的一些量是:
1. 素数p和q(保密的);
2. n=p*q(公开的);
3. φ(n)=(p-1)*(q-1)(保密的);
4. 加密密钥e(公开的)要满足0<e<φ(n), 且e和φ(n)的最大公约数为1(互素);
5. 解密密钥d(保密的)要满足0<d<φ(n), 且d*e mod φ(n) = 1
如果用M代表明文,C代表密文,E(M)代表对明文加密运算,D(C)代表对密文解密运算,则有:
E(M)=M^e mod n=C
D(C)=C^d mod n=M
RSA算法安全性的理论基础是大数的因子分解问题至今没有很好的算法,因而公开e和n不易求出p、q及d。RSA算法要求p和q是两个足够大的素数(例如100位十进制数)且长度相差比较小
2.5单向哈希函数
在很多情况下,我们需要鉴别和认证用户。如登陆计算机(自动柜员机)时,计算机往往需要知道用户是谁,确认某个用户而不是其他人冒充,传统的方法是用口令来解决这个问题。用户在登陆计算机时输入口令,有计算机确认确认口令正确后,用户才可登陆计算机。用户和计算机均需知道口令。用户每次登陆均需输入口令。由于计算机需要知道口令,这就需要把口令保存在计算机中。这为入侵计算机偷取口令提供了可能。为此,我们不直接保存口令本身,而保存口令的散列值(口令的某种表示形式)。当用户输入口令后,计算机先计算口令的散列值并于保存在计算集中的散列值进行比较,以次来鉴别用户。由于用来计算散列的值的函数具有单向性,即根据散列值不可能逆向恢复出口令,从而即使获得了有口令产生的散列值也无法知道用户的口令
单向散列函数 H(M) 作用于一个任意长度的消息 M,它返回一个固定长度的散列值 h,其中 h 的长度为 m 。
输入为任意长度且输出为固定长度的函数有很多种,但单向散列函数还有使其单向的其它特性:
(1) 给定 M ,很容易计算 h ;
(2) 给定 h ,根据 H(M) = h 计算 M 很难;
(3) 给定 M ,要找到另一个消息 M' 并满足 H(M) = H(M') 很难。
在许多应用中,仅有单向性是不够的,还需要称之为"抗碰撞"的条件:
要找出两个随机的消息 M 和 M',使 H(M) = H(M') 满足很难。
由于散列函数的这些特性,由于公开密码算法的计算速度往往很慢,所以,在一些密码协议中,它可以作为一个消息 M 的摘要,代替原始消息 M,让发送者为 H(M) 签名而不是对 M 签名。
如 SHA 散列算法用于数字签名协议 DSA中
2.6数字签名
提到数字签名就离不开公开密码系统和散列技术。
有几种公钥算法能用作数字签名。在一些算法中,例如RSA,公钥或者私钥都可用作加密。用你的私钥加密文件,你就拥有安全的数字签名。在其它情况下,如DSA,算法便区分开来了数字签名算法不能用于加密。这种思想首先由Diffie和Hellman提出。
基本协议是简单的:
(1) A 用她的私钥对文件加密,从而对文件签名。
(2) A 将签名的文件传给B。
(3) B用A的公钥解密文件,从而验证签名。
这个协议中,只需要证明A的公钥的确是她的。如果B不能完成第(3)步,那么他知道签名是无效的。
这个协议也满足以下特征:
(1) 签名是可信的。当B用A的公钥验证信息时,他知道是由A签名的。
(2) 签名是不可伪造的。只有A知道她的私钥。
(3) 签名是不可重用的。签名是文件的函数,并且不可能转换成另外的文件。
(4) 被签名的文件是不可改变的。如果文件有任何改变,文件就不可能用A的公钥验证。
(5) 签名是不可抵赖的。B不用A的帮助就能验证A的签名。
在实际应用中,因为公共密码算法的速度太慢,签名者往往是对消息的散列签名而不是对消息本身签名。这样做并不会降低签名的可信性
目前有许多种技术保证信息的安全不受侵犯,例如加密技术、访问控制技术、认证技术以及安全审计技术等,但这些技术大多数是用来预防用的,信息一旦被攻破,我们不能保证信息的完整性。为此,一种新兴的用来保证信息完整性的安全技术——数字签名技术成为人们非常关心的话题。那么,什么是数字签名技术?它有什么特殊功能呢?
概念
在数字签名技术出现之前,曾经出现过一种“数字化签名”技术,简单地说就是在手写板上签名,然后将图像传输到电子文档中,这种“数字化签名”可以被剪切,然后粘贴到任意文档上,这样非法复制变得非常容易,所以这种签名的方式是不安全的。数字签名技术与数字化签名技术是两种截然不同的安全技术,数字签名与用户的姓名和手写签名形式毫无关系,它实际使用了信息发送者的私有密钥变换所需传输的信息。对于不同的文档信息,发送者的数字签名并不相同。没有私有密钥,任何人都无法完成非法复制。从这个意义上来说,“数字签名”是通过一个单向函数对要传送的报文进行处理得到的,用以认证报文来源并核实报文是否发生变化的一个字母数字串。
原理
该技术在具体工作时,首先发送方对信息施以数学变换,所得的信息与原信息惟一对应;在接收方进行逆变换,得到原始信息。只要数学变换方法优良,变换后的信息在传输中就具有很强的安全性,很难被破译、篡改。这一个过程称为加密,对应的反变换过程称为解密。
现在有两类不同的加密技术,一类是对称加密,双方具有共享的密钥,只有在双方都知道密钥的情况下才能使用,通常应用于孤立的环境之中,比如在使用自动取款机(ATM)时,用户需要输入用户识别号码(PIN),银行确认这个号码后,双方在获得密码的基础上进行交易,如果用户数目过多,超过了可以管理的范围时,这种机制并不可靠。
另一类是非对称加密,也称为公开密钥加密,密钥是由公开密钥和私有密钥组成的密钥对,用私有密钥进行加密,利用公开密钥可以进行解密,但是由于公开密钥无法推算出私有密钥,所以公开的密钥并不会损害私有密钥的安全,公开密钥无须保密,可以公开传播,而私有密钥必须保密,丢失时需要报告鉴定中心及数据库。
算法
数字签名的算法很多, 应用最为广泛的三种是: Hash签名、DSS签名和RSA签名。
1. Hash签名
Hash签名不属于强计算密集型算法,应用较广泛。它可以降低服务器资源的消耗,减轻中央服务器的负荷。Hash的主要局限是接收方必须持有用户密钥的副本以检验签名, 因为双方都知道生成签名的密钥,较容易攻破,存在伪造签名的可能。
2. DSS和RSA签名
DSS和RSA采用了公钥算法,不存在Hash的局限性。RSA是最流行的一种加密标准,许多产品的内核中都有RSA的软件和类库。早在Web飞速发展之前,RSA数据安全公司就负责数字签名软件与Macintosh操作系统的集成,在Apple的协作软件PowerTalk上还增加了签名拖放功能,用户只要把需要加密的数据拖到相应的图标上,就完成了电子形式的数字签名。与DSS不同,RSA既可以用来加密数据,也可以用于身份认证。和Hash签名相比,在公钥系统中,由于生成签名的密钥只存储于用户的计算机中,安全系数大一些。
功能
数字签名可以解决否认、伪造、篡改及冒充等问题。具体要求:发送者事后不能否认发送的报文签名、接收者能够核实发送者发送的报文签名、接收者不能伪造发送者的报文签名、接收者不能对发送者的报文进行部分篡改、网络中的某一用户不能冒充另一用户作为发送者或接收者。数字签名的应用范围十分广泛,在保障电子数据交换(EDI)的安全性上是一个突破性的进展,凡是需要对用户的身份进行判断的情况都可以使用数字签名,比如加密信件、商务信函、定货购买系统、远程金融交易、自动模式处理等等。
缺憾
数字签名的引入过程中不可避免地会带来一些新问题,需要进一步加以解决,数字签名需要相关法律条文的支持。
1. 需要立法机构对数字签名技术有足够的重视,并且在立法上加快脚步,迅速制定有关法律,以充分实现数字签名具有的特殊鉴别作用,有力地推动电子商务以及其他网上事务的发展。
2. 如果发送方的信息已经进行了数字签名,那么接收方就一定要有数字签名软件,这就要求软件具有很高的普及性。
3. 假设某人发送信息后脱离了某个组织,被取消了原有数字签名的权限,以往发送的数字签名在鉴定时只能在取消确认列表中找到原有确认信息,这样就需要鉴定中心结合时间信息进行鉴定。
4. 基础设施(鉴定中心、在线存取数据库等)的费用,是采用公共资金还是在使用期内向用户收费?如果在使用期内收费,会不会影响到这项技术的全面推广?
实施
实现数字签名有很多方法,目前采用较多的是非对称加密技术和对称加密技术。虽然这两种技术实施步骤不尽相同,但大体的工作程序是一样的。用户首先可以下载或者购买数字签名软件,然后安装在个人电脑上。在产生密钥对后,软件自动向外界传送公开密钥。由于公共密钥的存储需要,所以需要建立一个鉴定中心(CA)完成个人信息及其密钥的确定工作。鉴定中心是一个政府参与管理的第三方成员,以便保证信息的安全和集中管理。用户在获取公开密钥时,首先向鉴定中心请求数字确认,鉴定中心确认用户身份后,发出数字确认,同时鉴定中心向数据库发送确认信息。然后用户使用私有密钥对所传信息签名,保证信息的完整性、真实性,也使发送方无法否认信息的发送,之后发向接收方;接收方接收到信息后,使用公开密钥确认数字签名,进入数据库检查用户确认信息的状况和可信度;最后数据库向接收方返回用户确认状态信息。不过,在使用这种技术时,签名者必须注意保护好私有密钥,因为它是公开密钥体系安全的重要基础。如果密钥丢失,应该立即报告鉴定中心取消认证,将其列入确认取消列表之中。其次,鉴定中心必须能够迅速确认用户的身份及其密钥的关系。一旦接收到用户请求,鉴定中心要立即认证信息的安全性并返回信息。



