K-means聚类算法及python代码实现

K-means聚类算法（事先数据并没有类别之分！所有的数据都是一样的）

1、概述

K-means算法是集简单和经典于一身的基于距离的聚类算法

采用距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越大。

该算法认为类簇是由距离靠近的对象组成的，因此把得到紧凑且独立的簇作为最终目标。

 

2、核心思想

通过迭代寻找k个类簇的一种划分方案，使得用这k个类簇的均值来代表相应各类样本时所得的总体误差最小。

k个聚类具有以下特点：各聚类本身尽可能的紧凑，而各聚类之间尽可能的分开。

 k-means算法的基础是最小误差平方和准则,

其代价函数是：

    

       式中，μc(i)表示第i个聚类的均值。

各类簇内的样本越相似，其与该类均值间的误差平方越小，对所有类所得到的误差平方求和，即可验证分为k类时，各聚类是否是最优的。

上式的代价函数无法用解析的方法最小化，只能有迭代的方法。

 

3、算法步骤图解

下图展示了对n个样本点进行K-means聚类的效果，这里k取2。

 

 

4、算法实现步骤

k-means算法是将样本聚类成 k个簇（cluster），其中k是用户给定的，其求解过程非常直观简单，具体算法描述如下：

1) 随机选取 k个聚类质心点

2) 重复下面过程直到收敛  {

      对于每一个样例 i，计算其应该属于的类：

        

      对于每一个类 j，重新计算该类的质心：

         

  }

   

其伪代码如下：

******************************************************************************

创建k个点作为初始的质心点（随机选择）

当任意一个点的簇分配结果发生改变时

       对数据集中的每一个数据点

              对每一个质心

                     计算质心与数据点的距离

              将数据点分配到距离最近的簇

       对每一个簇，计算簇中所有点的均值，并将均值作为质心

********************************************************

 

5、K-means聚类算法python实战

需求：

对给定的数据集进行聚类

本案例采用二维数据集，共80个样本，有4个类。

#!/usr/bin/python
# coding=utf-8
from numpy import *
# 加载数据
def loadDataSet(fileName):  # 解析文件，按tab分割字段，得到一个浮点数字类型的矩阵
    dataMat = []              # 文件的最后一个字段是类别标签
    fr = open(fileName)
    for line in fr.readlines():
        curLine = line.strip().split('\t')
        fltLine = map(float, curLine)    # 将每个元素转成float类型
        dataMat.append(fltLine)
    return dataMat

# 计算欧几里得距离
def distEclud(vecA, vecB):
    return sqrt(sum(power(vecA - vecB, 2))) # 求两个向量之间的距离

# 构建聚簇中心，取k个(此例中为4)随机质心
def randCent(dataSet, k):
    n = shape(dataSet)[1]
    centroids = mat(zeros((k,n)))   # 每个质心有n个坐标值，总共要k个质心
    for j in range(n):
        minJ = min(dataSet[:,j])
        maxJ = max(dataSet[:,j])
        rangeJ = float(maxJ - minJ)
        centroids[:,j] = minJ + rangeJ * random.rand(k, 1)
    return centroids

# k-means 聚类算法
def kMeans(dataSet, k, distMeans =distEclud, createCent = randCent):
    m = shape(dataSet)[0]
    clusterAssment = mat(zeros((m,2)))    # 用于存放该样本属于哪类及质心距离
    # clusterAssment第一列存放该数据所属的中心点，第二列是该数据到中心点的距离
    centroids = createCent(dataSet, k)
    clusterChanged = True   # 用来判断聚类是否已经收敛
    while clusterChanged:
        clusterChanged = False;
        for i in range(m):  # 把每一个数据点划分到离它最近的中心点
            minDist = inf; minIndex = -1;
            for j in range(k):
                distJI = distMeans(centroids[j,:], dataSet[i,:])
                if distJI < minDist:
                    minDist = distJI; minIndex = j  # 如果第i个数据点到第j个中心点更近，则将i归属为j
            if clusterAssment[i,0] != minIndex: clusterChanged = True;  # 如果分配发生变化，则需要继续迭代
            clusterAssment[i,:] = minIndex,minDist**2   # 并将第i个数据点的分配情况存入字典
        print centroids
        for cent in range(k):   # 重新计算中心点
            ptsInClust = dataSet[nonzero(clusterAssment[:,0].A == cent)[0]]   # 去第一列等于cent的所有列
            centroids[cent,:] = mean(ptsInClust, axis = 0)  # 算出这些数据的中心点
    return centroids, clusterAssment
# --------------------测试----------------------------------------------------
# 用测试数据及测试kmeans算法
datMat = mat(loadDataSet('testSet.txt'))
myCentroids,clustAssing = kMeans(datMat,4)
print myCentroids
print clustAssing

 

运行结果：

 

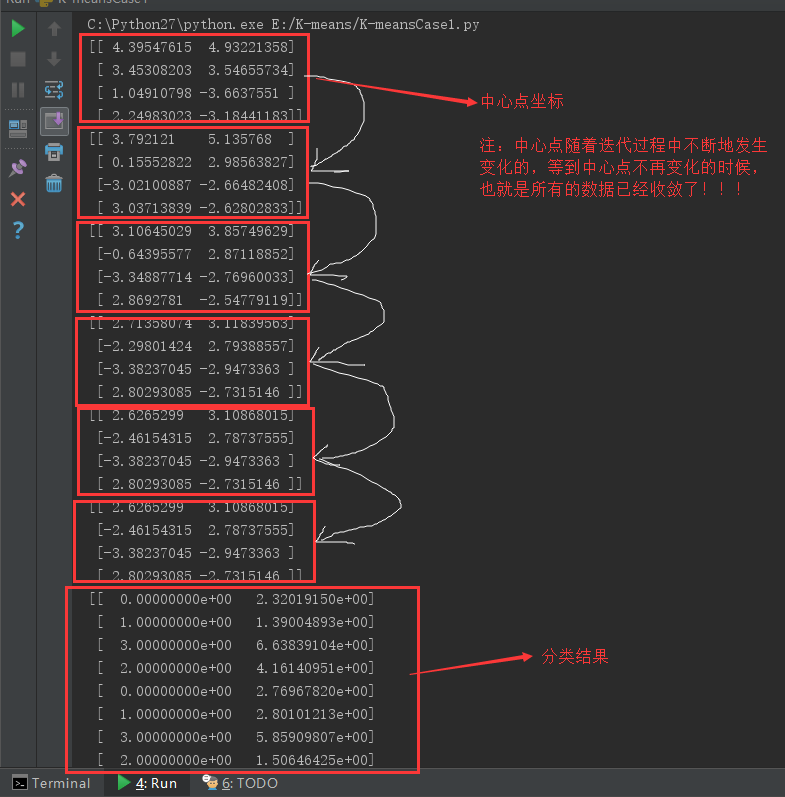
6、K-means算法补充

K-means算法的缺点及改进方法

（1）k值的选择是用户指定的，不同的k得到的结果会有挺大的不同，如下图所示，左边是k=3的结果，这个就太稀疏了，蓝色的那个簇其实是可以再划分成两个簇的。而右图是k=5的结果，可以看到红色菱形和蓝色菱形这两个簇应该是可以合并成一个簇的：

改进：

对k的选择可以先用一些算法分析数据的分布，如重心和密度等，然后选择合适的k

 

 

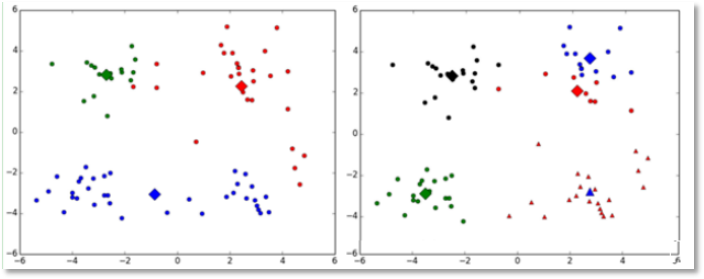
（2）对k个初始质心的选择比较敏感，容易陷入局部最小值。例如，我们上面的算法运行的时候，有可能会得到不同的结果，如下面这两种情况。K-means也是收敛了，只是收敛到了局部最小值：

改进：

 

有人提出了另一个成为二分k均值（bisecting k-means）算法，它对初始的k个质心的选择就不太敏感

 

 

（3）存在局限性，如下面这种非球状的数据分布就搞不定了：

 

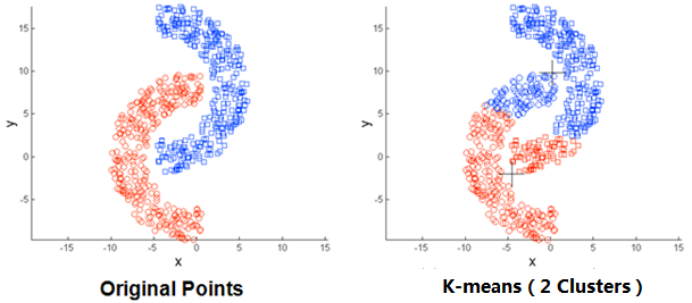
（4）数据集比较大的时候，收敛会比较慢。

 

---

 

上班了，工作繁忙，很少看博客了，不能及时给各位数据集，很抱歉，现在决定放在博客里面，大家复制下去使用即可：testSet.txt

1.658985    4.285136
-3.453687    3.424321
4.838138    -1.151539
-5.379713    -3.362104
0.972564    2.924086
-3.567919    1.531611
0.450614    -3.302219
-3.487105    -1.724432
2.668759    1.594842
-3.156485    3.191137
3.165506    -3.999838
-2.786837    -3.099354
4.208187    2.984927
-2.123337    2.943366
0.704199    -0.479481
-0.392370    -3.963704
2.831667    1.574018
-0.790153    3.343144
2.943496    -3.357075
-3.195883    -2.283926
2.336445    2.875106
-1.786345    2.554248
2.190101    -1.906020
-3.403367    -2.778288
1.778124    3.880832
-1.688346    2.230267
2.592976    -2.054368
-4.007257    -3.207066
2.257734    3.387564
-2.679011    0.785119
0.939512    -4.023563
-3.674424    -2.261084
2.046259    2.735279
-3.189470    1.780269
4.372646    -0.822248
-2.579316    -3.497576
1.889034    5.190400
-0.798747    2.185588
2.836520    -2.658556
-3.837877    -3.253815
2.096701    3.886007
-2.709034    2.923887
3.367037    -3.184789
-2.121479    -4.232586
2.329546    3.179764
-3.284816    3.273099
3.091414    -3.815232
-3.762093    -2.432191
3.542056    2.778832
-1.736822    4.241041
2.127073    -2.983680
-4.323818    -3.938116
3.792121    5.135768
-4.786473    3.358547
2.624081    -3.260715
-4.009299    -2.978115
2.493525    1.963710
-2.513661    2.642162
1.864375    -3.176309
-3.171184    -3.572452
2.894220    2.489128
-2.562539    2.884438
3.491078    -3.947487
-2.565729    -2.012114
3.332948    3.983102
-1.616805    3.573188
2.280615    -2.559444
-2.651229    -3.103198
2.321395    3.154987
-1.685703    2.939697
3.031012    -3.620252
-4.599622    -2.185829
4.196223    1.126677
-2.133863    3.093686
4.668892    -2.562705
-2.793241    -2.149706
2.884105    3.043438
-2.967647    2.848696
4.479332    -1.764772
-4.905566    -2.911070

 

---