机器学习之LR算法理论和实战(理论篇)
1. LR算法简述
LR 全称Logistic Regression,我们喜欢称她为逻辑回归或者逻辑斯蒂克回归,是传统机器学习中的最简单的最常用的分类模型。总之,LR算法简单、高效、易于并行且在线学习的特点,在工业界具有非常广泛的应用。在线学习指得是:可以利用新的数据对各个特征的权重进行更新,而不需要重新利用历史数据训练。
LR适用于各项广义上的分类任务,,如:评论信息正负情感分析(二分类)、用户点击率(二分类)、用户违约信息预测(二分类)、用户等级分类(多分类 )等场景;
实际开发中,一般针对该类任务首先都会构建一个基于LR的模型作为Baseline Model,实现快速上线,然后在此基础上结合后续业务与数据的演进,不断的优化改进。
2. 符号约定
本文 行向量 都是 \(W^T\) \(X_i^{T}\), 都是加了T; 列向量 都是 \(W\), \(X_i\),\(Y_i\),\(y_i\),\(x_i\),都不加T,也有例外,如\(Y=(Y_1,Y_2,...,Y_m)\)则是行向量,反正这违反这一约定的情况下,一定会在旁边说明
3. LR的理论基础
主要用于二分类算法,不妨用 1 0 表示两个类
sigmoid函数
不妨记sigmoid 为 \(\sigma\)
sigmoid 函数图像:
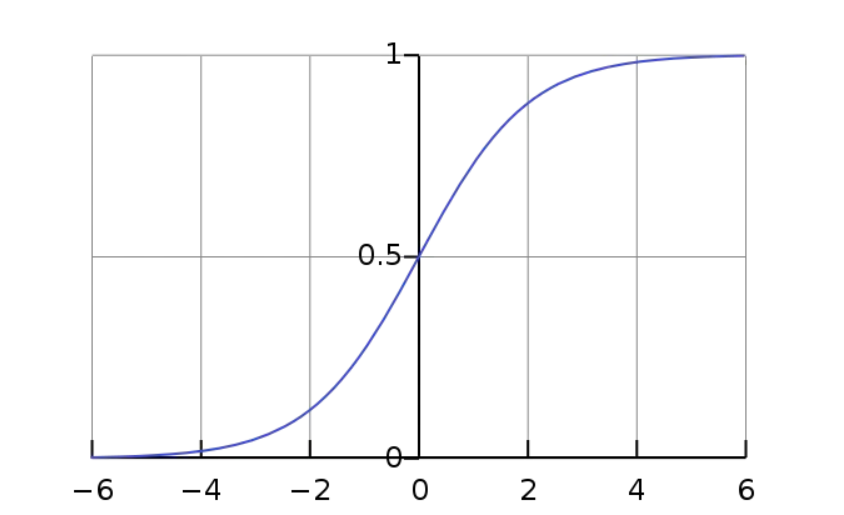
sigmoid 导函数图像:
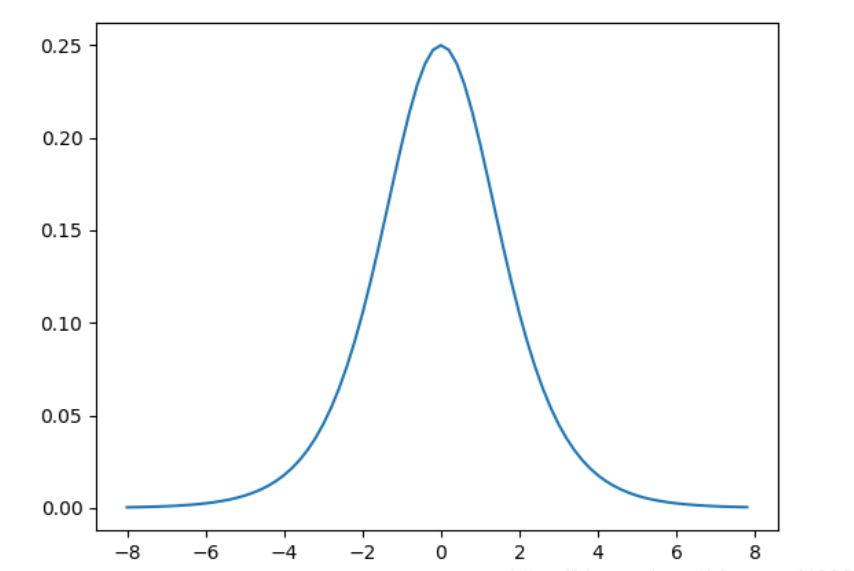
注意到sigmoid函数一下性质:(W表示列向量,\(W^T\)表示行向量)
(1) \(\sigma(0) = \frac{1}{2}\);
(2) sigmoid函数关于点(0,\(\frac{1}{2}\))对称,故存在\(\sigma(x) + \sigma(-x) = 1\)
(2) \(\sigma\)函数为当趋近于-6时,y趋于0,当sigmoid函数趋于6时,y趋于1;
(3) \(\sigma^{'}(x) = \sigma(x)(1 - \sigma(x))\)
(4) sigmoid导函数为偶函数,且恒大于0;
3.1 LR算法
对于一个样本,记为\((X_{i},Y_{i})\),\(Y_{i}\)取0或1.\(X_{i}=<1,x_1,x_2,...x_n>\),参数\(W=<w_0,w_1,w_2,...,w_n>\)
\(w_0 + w_1 \times x_1 + w_2 \times x_2 + ... + w_n \times x_n\) = \(W^T \times X\)
\(\hat{Y} = \sigma(W^T \times X)\)
当 \(\hat{Y} < 0.5\) 分为负类 0;
当 \(\hat{Y} > 0.5\) 分为正类 1;
利用极大似然估计(如果发生,就让其发生的可能最大),LR的目标函数为:
当\(\hat{Y_{i}} = 1\)时:
当\(\hat{Y_{i}} = 0\)时:
故综合(1)(2)式子得:
- 注:
因为,预测值\(Y_{i}\)只有两种可能,0 或者 1.
所以,当 \(Y_{i} = 0\)时:
当\(Y_{i} = 1\)时:
故(3)式是(1)(2)两种情况统一写法。
不仿令\(h_{W}(X_i) = \hat{Y} = P(Y_{i} | X_{i};W)\),故所有样本的损失函数为:
这个是模型已知,求参数,使得L(W)最大,对等式(4)取log,不影响 W 的取值,故可以等价于 :
即为:
注意,这里 \(h_{w}(X_{i})\) 为 \(\hat{Y_{i}}\) 是预测值, 而 \(Y_{i}\)是样本中打得标签,已知的哦,千万不要混淆。
(4)式子为最终需要的损失函数,下面利用随机梯度下降法,更新参数,
易得:标量对向量的求导参见:https://www.cnblogs.com/pinard/p/10750718.html
特别地:
故参数更新公式得:
其中 \(\alpha\)是学习率,取正数,需要我们手动设定。
3.2 LR算法训练过程(伪代码描述)
- 初始化参数 \(W_{0}\) ,\(\alpha\),初始化预估训练轮数 epoch
- 向量化(不使用用for,for不利于cuda并行化):
\(X = [X_1,X_2,...X_m]\), \(Y = (Y_1,Y_2,...Y_m)\) 其中 \(Y_i\) 取 0 或者 1故,Y就是行向量。
for i=0 to epoch:
\(\qquad step1: A = \hat{Y} = \sigma(W_{i}^T \times X)\) 说明: 其中A是行向量。
\(\qquad step2: log(A)\) , \(log(1 - A)\) 说明: 其中(1-A)是标量1减去行向量A,用到了编程语言的广播机制, 注意log(A) log(1 - A) 是行向量哦。
\(\qquad step3: J(W) = Y (log (A)^T) + (1 - Y)(log(1 - A)^T)\) 说明:注意这里的Y是行向量,其中 1- A是标量1减去行向量A,用到了编程语言的广播机制,特别地,这里的Y,1 - Y都是行向量,和符号规定有点出入。
\(\qquad step4: dW = \frac{\partial{J}}{\partial{W}} =(Y - \hat{Y}) X^T\)
\(\qquad step5: W_{i} = W_{i-1} + \alpha dW\) 说明:\(\alpha\) 统一设置为正数, 梯度上升求最大值
当达到一定准确率,或者其他性能指标时,停止训练,保存\(W_{i}\)值,即为\(W_f\),解可得训练的最终模型为:
当 \(\sigma(X) > 0.5\) ,预测Y 为 1;反之,预测Y为0.
对于step3的解释:
我们将\(J(W) = \sum_{i}^{m} Y_{i}log(\sigma(W^TX_{i})) + (1 - Y_{i})log(1 - \sigma(W^TX_{i})) (5)\) 中的 \(\sum_{i} ^{m}\)向量化了,不然需要写个for,不利于cuda并行。
其中 \(a_i = \sigma(W_i^T X_i)\)
对于step4的解释:
我们将\((6)式 = \frac{\partial{J}}{\partial{W}} = \sum_{i}^{m}((Y_{i} - \hat{Y_{i}}) X_i) (7)\) 中的 \(\sum_{i} ^{m}\)向量化了。其中 \((Y - \hat{Y})\) X^T,可以写成:
即为:
4. 参考文献
[1] https://www.jianshu.com/p/dce9f1af7bc9
[2] https://www.cnblogs.com/pinard/p/10750718.html(标量对矩阵的求导)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号