决策树学习记录---分裂信息

分裂信息的探索：

分裂信息公式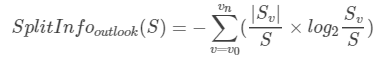：，下面我对分裂信息进行一个可视化。

首先我假设有100个样本， 在不同的特征数目下，计算分裂信息，为了计算方便，在此我定义每个特征值下面的样本个数是相同的

代码：

import math
import matplotlib.pyplot as plt

x = [2, 4, 10, 20, 50, 100]     # 特征值个数初始化
y = []  # 对应不同特征值个数的分裂信息计算初始化

def caculate(total, num):
    '''
    total :样本总数
    num :特征值个数
    '''
    reve = total/num  #每个特征值下面的样本数
    return -(reve/total)*math.log(reve/total)*num

for i in range(len(x)):     # 计算y
    y.append(caculate(100, x[i]))
    
plt.figure()
plt.plot(x, y)
plt.xlabel('特征值个数')
plt.ylabel('分裂信息')
plt.show()

结果：

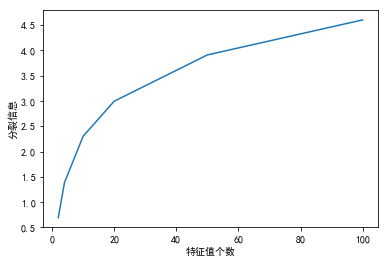
由以上结果大概可知：一个特征下面的特征值越多，这个特征的分裂信息就越大。

 

当然还有一个维度我并没有考虑进去， 那就是如果一个特征有同样数量的特征值，但是特征值下面的样本数不一样，那么分裂信息的值如何变化？

首先我假设，我有100个样本，某个特征下面有两个特征值，不同特征值对应的样本数从1-50变化，观察分裂信息如何变化。

代码：

import math
import matplotlib.pyplot as plt
import numpy as np

totalNum = 100  # 样本总数初始化为100
midNum = totalNum / 2   # 样本总数中值

x1 = np.arange(midNum+1)     # 特征值个数初始化
x1 = x1[1:]     # [1,2,3,4.....50]
x2 = 100 - x1  # 对应不同特征值个数的分裂信息计算初始化[99,98,97......50]
y = []
def caculate(total, num1, num2):
    '''
    total : 样本总数
    num1 : 特征值1样本个数
    num2 : 特征值2样本个数
    '''
    return -(num1/total)*math.log(num1/total) - (num2/total)*math.log(num2/total)

for i in range(len(x1)):     # 计算y
    y.append(caculate(100, x1[i], x2[i]))
    
plt.figure()
plt.plot(x1, y)
plt.xlabel('特征值样本数相似程度(->大)')
plt.ylabel('分裂信息')
plt.show()
 

　　

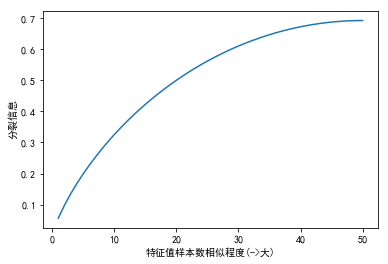
由上图可知，当不同特征值的样本个数越接近， 分裂信息就越大。