题解 CF36B【Fractal】

思路：暴力模拟。

---

看到题解大多是从大到小分析位置输出答案，这里特别提供一种简洁易懂的暴力模拟涂色方法。

根据题目上的涂色方式，我们可以想到一种模拟：对于原图每一个白块，我们可以在新图上把它替换成单位正方形；对于原图每一个黑块，我们可以在新图上把它替换成 $ n \times n $ 的全黑正方形。

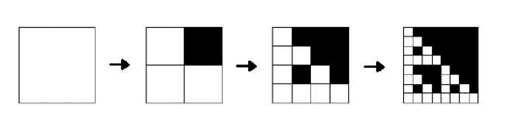
具体实现，我们需要开最多五层数组，每次从当前图向下一层图涂色时，注意当前色块放大后在新图的位置。具体来讲，对于原图的色块 \((i,j)\) ，当 n=2 时，它在新图中的位置是 $ (i\times 2-1,j\times 2-1)\(~\) (i,j) $ 的正方形，当 n=3 时，它在新图中的位置是 $ (i\times 3-2,j\times 3-2)\(~\) (i,j) $ 的正方形。

剩下的就没有什么技术含量了，具体见代码。

Code：

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
inline int read() {
	int sum=0,w=1;
	char ch=getchar();
	while(ch<'0'||ch>'9') {
		if(ch=='-') w=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9') {
		sum=(sum<<3)+(sum<<1)+ch-'0';
		ch=getchar();
	}
	return sum*w;
}
int n,k,m=1;
char ans[6][300][300];
int main() {
    freopen("input.txt","r",stdin);
	freopen("output.txt","w",stdout);
	n=read(),k=read();
	for(int i=1; i<=n; i++) scanf("%s",ans[1][i]+1);
	for(int p=1; p<k; p++) {//涂色的层数，因为单位正方形是第一轮涂色，所以 <k 。
		m*=n;//m=n^p
		for(int i=1; i<=m; i++)
			for(int j=1; j<=m; j++) {
				if(ans[p][i][j]=='.') {
					if(n==2) {//对于 n=2 的情况暴力涂色。
						ans[p+1][i*n-1][j*n-1]=ans[1][1][1];
						ans[p+1][i*n][j*n-1]=ans[1][2][1];
						ans[p+1][i*n-1][j*n]=ans[1][1][2];
						ans[p+1][i*n][j*n]=ans[1][2][2];
					} else {//对于 n=3 的位置暴力涂色。
						ans[p+1][i*n-2][j*n-2]=ans[1][1][1];
						ans[p+1][i*n-1][j*n-2]=ans[1][2][1];
						ans[p+1][i*n][j*n-2]=ans[1][3][1];
						ans[p+1][i*n-2][j*n-1]=ans[1][1][2];
						ans[p+1][i*n-1][j*n-1]=ans[1][2][2];
						ans[p+1][i*n][j*n-1]=ans[1][3][2];
						ans[p+1][i*n-2][j*n]=ans[1][1][3];
						ans[p+1][i*n-1][j*n]=ans[1][2][3];
						ans[p+1][i*n][j*n]=ans[1][3][3];
					}
				} else {//全黑涂法
					if(n==2) {
						ans[p+1][i*n-1][j*n-1]='*';
						ans[p+1][i*n][j*n-1]='*';
						ans[p+1][i*n-1][j*n]='*';
						ans[p+1][i*n][j*n]='*';
					} else {
						ans[p+1][i*n-2][j*n-2]='*';
						ans[p+1][i*n-1][j*n-2]='*';
						ans[p+1][i*n][j*n-2]='*';
						ans[p+1][i*n-2][j*n-1]='*';
						ans[p+1][i*n-1][j*n-1]='*';
						ans[p+1][i*n][j*n-1]='*';
						ans[p+1][i*n-2][j*n]='*';
						ans[p+1][i*n-1][j*n]='*';
						ans[p+1][i*n][j*n]='*';
					}
				}
			}
	}
	for(int i=1; i<=m*n; i++) printf("%s\n",ans[k][i]+1);
	return 0;
}