2.14 比赛题解
总体概述
难度
- C 东方绯想天 入门
- E 东方鬼形兽 入门
- D 东方辉针城 入门
- A 东方红魔乡 普及-
- B 东方永夜抄 普及-
- G 东方茨歌仙 普及
- F 东方幻想麻雀 普及
- H 东方铃奈庵 普及+
是不是很水?没到300pts的非 20 级在役选手面壁思过!
下面按题目顺序进行讲解。
A 东方红魔乡
原题出自
2020牛客NOIP赛前集训营-普及组(第四场) B
想一下对于大小姐和二小姐的必胜策略。
对于大小姐
大小姐拿偶数个。首先,能一次性拿走的偶数个堆石子就一次性拿走,不给对方机会。其次,如果只有一堆偶数个石子,那么将其直接拿走就能获得胜利。
对于二小姐
二小姐拿奇数个。对于一堆奇数个石子,全部拿走不给对方机会。对于一堆偶数个石子,把它拆成 1 和 2n-1 (总 2n 个),这样可以保证必胜。
也就是说,如果只有一堆偶数个棋子,那么可以保证大小姐胜利。否则二小姐可以把任意一堆石子变成 1 ,导致大小姐不能获胜。
代码:
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
#define re register
#define pi pair<int,int>
#define F first
#define S second
using namespace std;
const int N=1000005;
inline int read() {
int sum=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9') {
if(ch=='-') w=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9') {
sum=(sum<<3)+(sum<<1)+ch-'0';
ch=getchar();
}
return sum*w;
}
int n,a;
int main() {
// freopen("hmx.in","r",stdin);
// freopen("hmx.out","w",stdout);
int t=read();
while(t--) {
n=read();
if(n==1) {
a=read();
if(a&1) puts("NO");
else puts("YES");
}
else {
while(n--) a=read();
puts("NO");
}
}
return 0;
}
B 东方永夜抄
原题出自
ZROI 2020 普及五连测 Day4 T1
很容易猜到一个结论,排序以后,直接按照顺序两两配对,而这确实是对的。
小证明:对于一个较小的数,与较大的数匹配一定比与更大的数匹配更优,这样会使差的绝对值的和更小。
代码:
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
#define re register
#define pi pair<int,int>
#define F first
#define S second
using namespace std;
const int N=200005;
inline int read() {
int sum=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9') {
if(ch=='-') w=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9') {
sum=(sum<<3)+(sum<<1)+ch-'0';
ch=getchar();
}
return sum*w;
}
int a[N];
int main() {
//freopen("yyc.in","r",stdin);
//freopen("yyc.out","w",stdout);
int n=read();
for(int i=1;i<=n;i++) a[i]=read();
sort(a+1,a+n+1);
int ans=0;
for(int i=1;i<n;i+=2) {
ans+=a[i+1]-a[i];
}
printf("%d",ans);
return 0;
}
C 东方绯想天
原题出自
@ahawzlc
设普通桃子个数为 \(m\) 个。
根据题目要求,使用“进位法”取整。
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
#define re register
#define pi pair<int,int>
#define F first
#define S second
using namespace std;
typedef long long ll;
const int N=200005;
inline ll read() {
ll sum=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9') {
if(ch=='-') w=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9') {
sum=(sum<<3)+(sum<<1)+ch-'0';
ch=getchar();
}
return sum*w;
}
ll n,a,b;
int main() {
// freopen("fxt.in","r",stdin);
// freopen("fxt.out","w",stdout);
n=read(),a=read(),b=read();
ll now=n*a*a*a,ans;
ans=now/(b*b*b);
if(b*b*b*ans==now) printf("%lld",ans);
else printf("%lld",ans+1);
return 0;
}
D 东方辉针城
原题出自
@ahawzlc
简要分析可得,只要点的高度大于下落时间 \(t\) ,那么这个点就可以被收取。(所以甚至一维数组都不用)
代码:
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
#define re register
#define pi pair<int,int>
#define F first
#define S second
using namespace std;
typedef long long ll;
typedef unsigned long long ul;
const int N=10005;
inline int read() {
int sum=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9') {
if(ch=='-') w=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9') {
sum=(sum<<3)+(sum<<1)+ch-'0';
ch=getchar();
}
return sum*w;
}
int x[N],y[N],ans;
int main() {
// freopen("hzc.in","r",stdin);
// freopen("hzc.out","w",stdout);
int n=read(),m=read(),q=read(),t=read();
for(int i=1;i<=q;i++) {
x[i]=read(),y[i]=read();
if(y[i]>t) ans++;
}
printf("%d",ans);
return 0;
}
E 东方鬼形兽
原题出自
@ahawzlc (不过似乎与别的题撞了)
以样例为例解释题目:
样例1 最少:
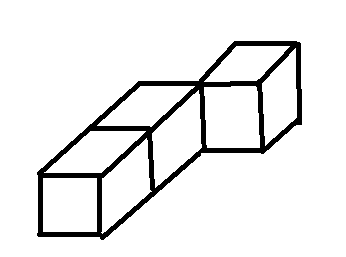
样例1 最多:
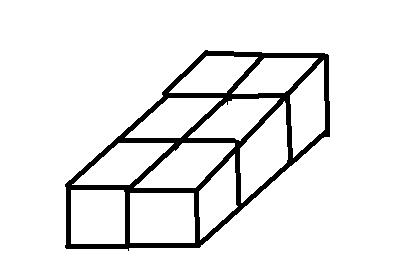
也就是说,最少时,每个方块至少独自承担了对主视图或对左视图的一个贡献,最多时的情况就是在最少时的情况把所有空间补全。
代码:
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
#define re register
#define pi pair<int,int>
#define F first
#define S second
using namespace std;
typedef long long ll;
typedef unsigned long long ul;
const int N=200005;
inline ll read() {
int sum=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9') {
if(ch=='-') w=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9') {
sum=(sum<<3)+(sum<<1)+ch-'0';
ch=getchar();
}
return sum*w;
}
int main() {
// freopen("gxs.in","r",stdin);
// freopen("gxs.out","w",stdout);
ll n=read(),m=read();
printf("%lld %lld",max(n,m),1ll*n*m);
return 0;
}
F 东方幻想麻雀
原题来自
@ahawzlc
字符串读入、存储、处理。没有幺九牌就是断幺九、有三个及以上暗刻就是三暗刻,只有一种颜色就是清一色。
具体实现参见代码
代码:
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
#define re register
#define pi pair<int,int>
#define F first
#define S second
using namespace std;
const int N=200005;
inline int read() {
int sum=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9') {
if(ch=='-') w=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9') {
sum=(sum<<3)+(sum<<1)+ch-'0';
ch=getchar();
}
return sum*w;
}
char c;
int mah[4][10],now,num;
bool z=0,dyj,sak,qys,m,p,s;
int main() {
for(int i=1;i<=18;i++) {
scanf("%c",&c);
if('0'<=c&&c<='9') mah[now][c-'0']++;
else now++;
}
for(int j=1;j<=7;j++) {
if(mah[3][j]) {
z=1;break;
}
}
if(mah[0][1]==0&&mah[0][9]==0&&mah[1][1]==0&&mah[1][9]==0&&mah[2][1]==0&&mah[2][9]==0&&!z) dyj=1;
for(int i=0;i<=3;i++) {
for(int j=1;j<=9;j++) {
if(mah[i][j]>=3) num++;
if(mah[0][j]) m=1;
if(mah[1][j]) p=1;
if(mah[2][j]) s=1;
}
}
if(num>=3) sak=1;
if((m&&!p&&!s&&!z)||(p&&!m&&!s&&!z)||(s&&!m&&!p&&!z)||(z&&!m&&!p&&!s)) qys=1;
if(dyj) printf("1");
if(sak) printf("2");
if(qys) printf("3");
if(!dyj&&!sak&&!qys) printf("NO");
return 0;
}
G 东方茨歌仙
原题出自
ZROI 2020 普及五连测 Day3 T1
你以为这只是个简单的数组模拟?ko no 离线处理 da!
直接使用数组模拟只有 60 pts,因为数组下标范围过于大,装不下。
所以考虑离线处理。
对于每一个查询,向前找最近的该点的修改,找不到为0。\(O(n^2)\)
原题作者说似乎可以使用二分优化,不知道这次有没有。\(O(log n)\)
当然可以直接用 map 。\(O(n)\)
代码 \(O(n^2)\) :
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
#define re register
#define pi pair<int,int>
#define F first
#define S second
using namespace std;
typedef long long ll;
typedef unsigned long long ul;
const int N=2005;
inline int read() {
int sum=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9') {
if(ch=='-') w=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9') {
sum=(sum<<3)+(sum<<1)+ch-'0';
ch=getchar();
}
return sum*w;
}
pi q[N];
int main() {
// freopen("cgx.in","r",stdin);
// freopen("cgx.out","w",stdout);
int n=read(),m=read();
for(int i=1;i<=n;i++) {
int opt=read();
if(opt==1) {
int x=read(),y=read();
q[i]=make_pair(x,y);
}
if(opt==2) {
int x=read();
bool ok=0;
for(int j=i-1;j>=1;j--) {
if(q[j].F==x) {
printf("%d\n",q[j].S);
ok=1;
break;
}
}
if(!ok) puts("0");
}
}
return 0;
}
H 东方铃奈庵
原题出自
@ahawzlc
部分分:
30pts 乱搞
第一个 20pts 输出 \(k\)
第二个 20pts 堆优 bfs
100pts 结构体堆优 bfs
100pts
因为小铃认为越近的点价值越高,所以bfs。
因为需要求最大价值,所以堆优。
因为同时需要最小花费,所以结构体,重定义小于号。
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
#define re register
#define pi pair<int,int>
#define F first
#define S second
#define mp make_pair
using namespace std;
typedef long long ll;
typedef unsigned long long ul;
const int N=1000005;
inline int read() {
int sum=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9') {
if(ch=='-') w=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9') {
sum=(sum<<3)+(sum<<1)+ch-'0';
ch=getchar();
}
return sum*w;
}
struct node {
int u,w,c;
};
bool operator < (const node &x,const node &y) {
if(x.w==y.w) return x.c>y.c;
return x.w<y.w;
}
priority_queue<node> q;
int n,k,w[N],c[N];
ll ans;
int cnt,h[N],nxt[N],to[N],rd[N];
void add(int x,int y) {
nxt[++cnt]=h[x],to[cnt]=y,h[x]=cnt;
}
bool vis[N];
void pro_bfs() {
int tot=0;
node p;
p.c=p.w=0,p.u=1;
q.push(p);
while(!q.empty()) {
int u=q.top().u;
q.pop();
tot++;
ans+=1ll*c[u];
vis[u]=1;
if(tot==k+1) return;
for(int i=h[u];i;i=nxt[i]) {
int v=to[i];
if(vis[v]) continue;
p.c=c[v],p.w=w[v],p.u=v;
q.push(p);
}
}
return;
}
int main() {
// freopen("lna.in","r",stdin);
// freopen("lna.out","w",stdout);
n=read(),k=read();
for(int i=1;i<=n;i++) c[i]=read();
for(int i=1;i<=n;i++) w[i]=read();
for(int i=1;i<n;i++) {
int x=read(),y=read();
add(x,y);
add(y,x);
}
pro_bfs();
printf("%lld",ans);
return 0;
}


