题解 P5097 【[USACO04OPEN]Cave Cows 2】

线段树解区间求值最好了！

---

简介：

线段树是一种用于区间求值的数据结构，基于二叉树，下面我简单介绍一下在本题中用于求最值的线段树：

线段树主要是承担\(\Theta(n\log n)\)区间（单点）修改和区间（单点）查询。

线段树示意图：

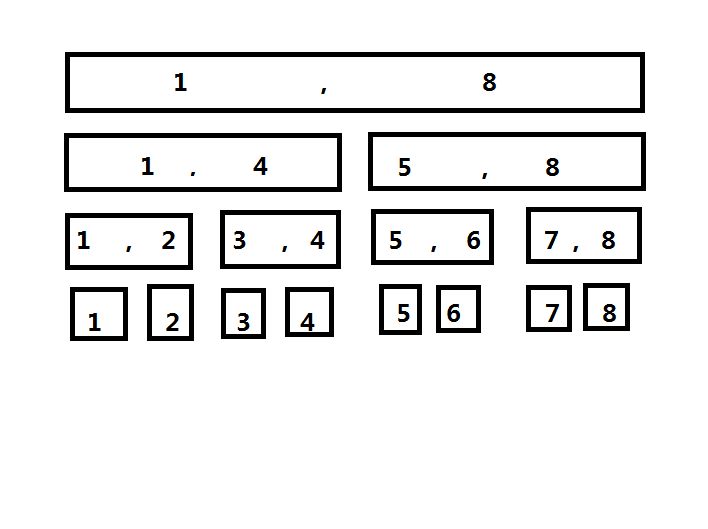
操作：

\(update\)

更新操作，是建树（\(build\)）和修改（\(change\)（本题中用不到））后更新线段树数值的操作。

\(build\)

建树操作，具体见代码

\(ask\)

询问操作，参考示意图。假如我们要求区间\([2,5]\)的最值，我们可以把区间拆成\([2],[3,4],[5]\)然后递归求。设要求\([x,y]\)的最值，那么只要是满足\([x\le l,r\le y]\)的节点，都可以纳入答案。我们不用递归到单点，如果有整段的，可以直接拿来用，这就是线段树的精髓罢。

代码：

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int MAXN=1000000007;
int va[25005];
struct linetree {
	int l,r,sum;//结构体，本节点维护l——r的最值，sum为本节点的数值
} tree[125005];
void update(int now,int lson,int rson) {//与模板最不同的地方就是这里了
	tree[now].sum=min(tree[lson].sum,tree[rson].sum);//当前节点是左右孩子的最小值
}
void build(int now,int l,int r) {//建树，now为当前节点编号
	tree[now].l=l;
	tree[now].r=r;
	if(l==r) {
		tree[now].sum=va[l];
		return;
	}
	int mid=(l+r)>>1;
	int lson=now<<1;//将左孩子定到2*now位置
	int rson=now<<1|1;//右孩子定到2*now+1位置
	build(lson,l,mid);//继续向下建树
	build(rson,mid+1,r);//同上
	update(now,lson,rson);//递归回来更新当前节点
}
int sum=MAXN;
void ask(int now,int x,int y) {//区间求最值
	if(x<=tree[now].l&&y>=tree[now].r) {//只要满足这个条件，就可以将它作为某段区间纳入答案
		sum=min(sum,tree[now].sum);
		return;
	}//见注释的解释
	int l=tree[now].l,r=tree[now].r;
	int mid=(l+r)>>1;
	int lson=now<<1;
	int rson=now<<1|1;//意义与建树是一样
	if(x<=mid) ask(lson,x,y);//运用二分原理
	if(y>mid) ask(rson,x,y);
}
signed main() {
	int n,m;
	cin>>n>>m;
	for(int i=1; i<=n; i++)
		cin>>va[i];
	build(1,1,n);//可以参考示例图
	for(int i=1; i<=m; i++) {
		int x,y;
		cin>>x>>y;
		sum=MAXN;
		ask(1,x,y);
		cout<<sum<<endl;
	}
	return 0;
}