【题解】ars[A001]相控阵
[DSOI Round #1]相控阵
题目背景
三个小时后，月球将突破地月洛希极限，地球将会变成一片火海，人类的文明将会在三天内断绝……
可是，勇敢的人类从未屈服，他们决定在月球上放置地球上所有的核弹。
人类的内斗从未停歇，即使在此时，核弹的密码还没有完全公布，破译密码的进程缓慢，只好使用相控阵来放置核弹。
题目描述
现在有 \(n\) 颗核弹密码已被破译，我们把每 \(5\) 枚核弹组合到一起，\(5\) 枚核弹（\(1 \sim 5,6 \sim 10,11\sim 15 ......\)）中，第一枚和第二枚，第二枚和第三枚……第五枚和第一枚之间存在潜在反应关系，可能会产生一定的强力反应。核弹有两种模式，只有两颗核弹处于 不同模式 下，核弹的潜在反应关系才会生效，产生强力反应。$ a_i $ 表示第 $ i $ 枚核弹和 $ i+1 $ 枚的潜在反应关系强度，即产生强力反应的效果。（ 特殊的，当 $ i $ 为 $ 5 $ 的倍数即为第 $ i $ 枚和第 $ i-4 $ 枚核弹产生强力反应的效果）。
相控阵对月球产生的作用力即为强力反应效果之和。你需要求出有多少种模式开启方案，使得两种模式的核弹数量相等，且总作用力最大，输出方案数模 $ 998244853 $ 的结果。
即使需要取模，也是人类最后的希望，请你……一定要在 1s 内求出结果啊。
输入格式
第一行一个整数 \(n\)， 代表核弹密码的总数
接下来 $ n $ 个正整数 $ a_i $，表示每条核弹密码产生的强力反应。
数据保证 $ n $ 是 $ 10 $ 的倍数。
输出格式
一行一个整数，表示答案对 \(998244853\) 取模的值。
样例 #1
样例输入 #1
10
6 4 5 6 3 2 8 2 3 6
样例输出 #1
4
提示
【样例解释】
样例1如图所示
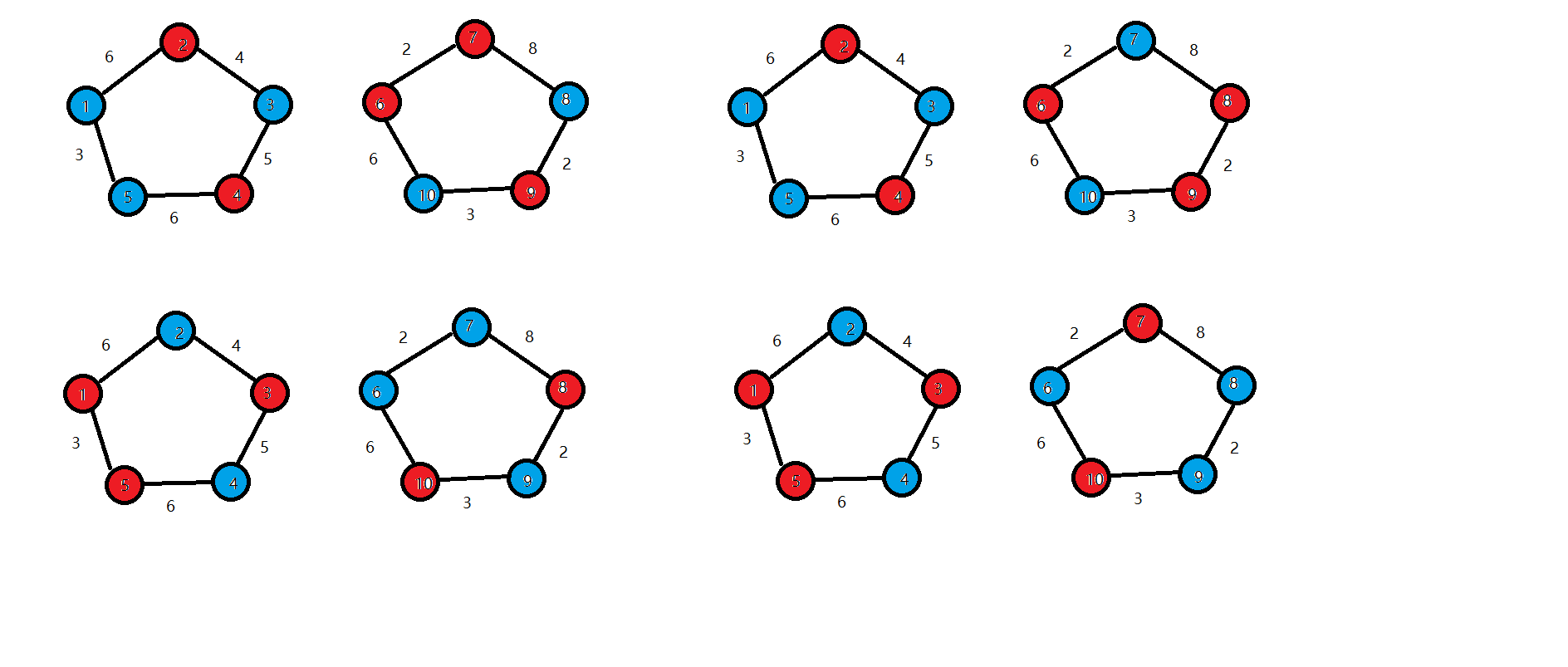
红色和蓝色分别为核弹的不同模式。
易求最大值为 \(40\)。
共有四种方案。
【数据约定】
对于 $ 20% $ 的数据，满足 $ n \le 20 $。
对于 $ 40% $ 的数据，满足 $ n \le 100 $。
对于 $ 60% $ 的数据，满足 $ n \le 5000 $。
对于全部数据，保证 \(10\leq n\leq 3 \times 10^5\)，\(1 \leq a_i \leq 10^3\)，并保证 \(n\) 是 \(10\) 的倍数。
逆元：
\(\frac{a}{b} \bmod m=a \times b^{-1} \bmod m\)
其中 \(m\) 为一个质数
定义 \(b^{-1}\) 为 \(b\) 在模 \(m\) 意义下的逆元
则 \(b^{-1}\times b \bmod m=1\)
费马小定理：
\(a^{m-1} \equiv 1 \bmod m \iff a\times a^{m-2} \equiv 1 \bmod m\)
即 \(a\) 在模 \(m\) 意义下的逆元为 \(a^{m-2}\)
提示：请仔细读题
模拟赛 T1
一道简单好想小可爱题。
首先我们很容易得到一个结论，就是若想使总作用力最大，那么五个核弹中一定会有四个反应关系去对总作用力产生贡献。
证明的话：
五个核弹相当于一个五元环，不同模式相当于对点进行染色，我们不妨规定两种模式分别染色为红和蓝。
因为边数 \(n\) 为 \(10\) 的倍数，所以我们规定总共有 \(2m\) 个五元环。所以若一个五元环染出 \(2\) 蓝 \(3\) 红，那么必有另一个五元环染成 \(3\) 蓝 \(2\) 红。
如果一个五元环染出 \(1\) 蓝 \(4\) 红，必有另一个是 \(4\) 蓝 \(1\) 红，那么只有其中两条边可以为总作用力产生贡献，必然不优。
若染出 \(5\) 红同理，必有另一个是 \(5\) 蓝，没有边可以贡献，必然不优。
那么我们就知道最大总作用力一定是由每个五元环的其中最大的 \(4\) 条边贡献的。
如果每个五元环选边方案固定，那么总方案数是 \(2m \choose m\) （\(2m\) 个五元环中 \(m\) 个染成 \(2\) 蓝 \(3\) 红，剩下 \(m\) 个染成 \(3\) 蓝 \(2\) 红）
这部分可以用逆元 \(O(n)\) 计算，不再赘述。
那么我们现在就要考虑对于每个五元环，我们有多少种方案。
因为每个五元环要选其中最大的 \(4\) 个边，那么也就意味着，我们一定不选最小的那个边。即最小边的左右点染为同色，若有多个值相等的最小边，则就有多种染色方案。
如图：
故我们将每个五元环内部的方案数乘上五元环染色分配方案数即为最终总方案数。
最后注意模数是 \(998244\) \(\color{red}\large8\) \(53\) 而不是 \(998244353\)
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int _ = 3e5 + 5;
const int mod = 998244853;
int n; int a[_];
int fac[_], inv[_];
int ans = 1;
void init() {
fac[0] = fac[1] = inv[0] = inv[1] = 1;
for(int i = 2; i <= n; ++i) fac[i] = fac[i - 1] * i % mod;
for(int i = 2; i <= n; ++i) inv[i] = (mod - mod / i) * inv[mod % i] % mod;
for(int i = 1; i <= n; ++i) inv[i] = inv[i - 1] * inv[i] % mod;
}
int C(int _n, int _m) {
return fac[_n] * inv[_m] % mod * inv[_n - _m] % mod;
}
signed main() {
ios::sync_with_stdio(false); cin.tie(0), cout.tie(0);
cin >> n;
for(int i = 1; i <= n; ++i)
cin >> a[i];
init();
for(int i = 1; i <= n; i += 5) {
sort(a + i, a + i + 5); int cnt = 1;
for(int j = i + 1; j <= i + 4; ++j)
if(a[j] == a[j - 1]) ++cnt;
else break;
ans *= cnt, ans %= mod;
}
ans = ans * C(n / 5, n / 10) % mod;
cout << ans << endl;
return 0;
}
总体来说难度 csp-s 第一题或者更简单，作为签到题很合适！一起来赞美良心出题人吧！
