AdaBoost

原创转载请注明出处：https://www.cnblogs.com/agilestyle/p/12996858.html

 

集成算法

在数据挖掘中，分类算法可以说是核心算法，其中 AdaBoost 算法与随机森林算法一样都属于分类算法中的集成算法。

集成的含义就是集思广益，博取众长，当我们做决定的时候，我们先听取多个专家的意见，再做决定。

集成算法通常有两种方式，

• 投票选举（bagging）
• 再学习（boosting）

投票选举的场景类似把专家召集到一个会议桌前，当做一个决定的时候，让 K 个专家（K 个模型）分别进行分类，然后选择出现次数最多的那个类作为最终的分类结果。

再学习相当于把 K 个专家（K 个分类器）进行加权融合，形成一个新的超级专家（强分类器），让这个超级专家做判断。

 

投票选举和再学习的区别

Bagging 在做投票选举的时候可以并行计算，也就是 K 个“专家”在做判断的时候是相互独立的，不存在依赖性。

Boosting 的含义是提升，它的作用是每一次训练的时候都对上一次的训练进行改进提升，在训练的过程中这 K 个“专家”之间是有依赖性的，当引入第 K 个“专家”（第 K 个分类器）的时候，实际上是对前 K-1 个专家的优化。

 

AdaBoost 的工作原理

AdaBoost 的英文全称是 Adaptive Boosting，中文含义是自适应提升算法。它由 Freund 等人于 1995 年提出，是对 Boosting 算法的一种实现。

Boosting 算法是集成算法中的一种，同时也是一类算法的总称。这类算法通过训练多个弱分类器，将它们组合成一个强分类器。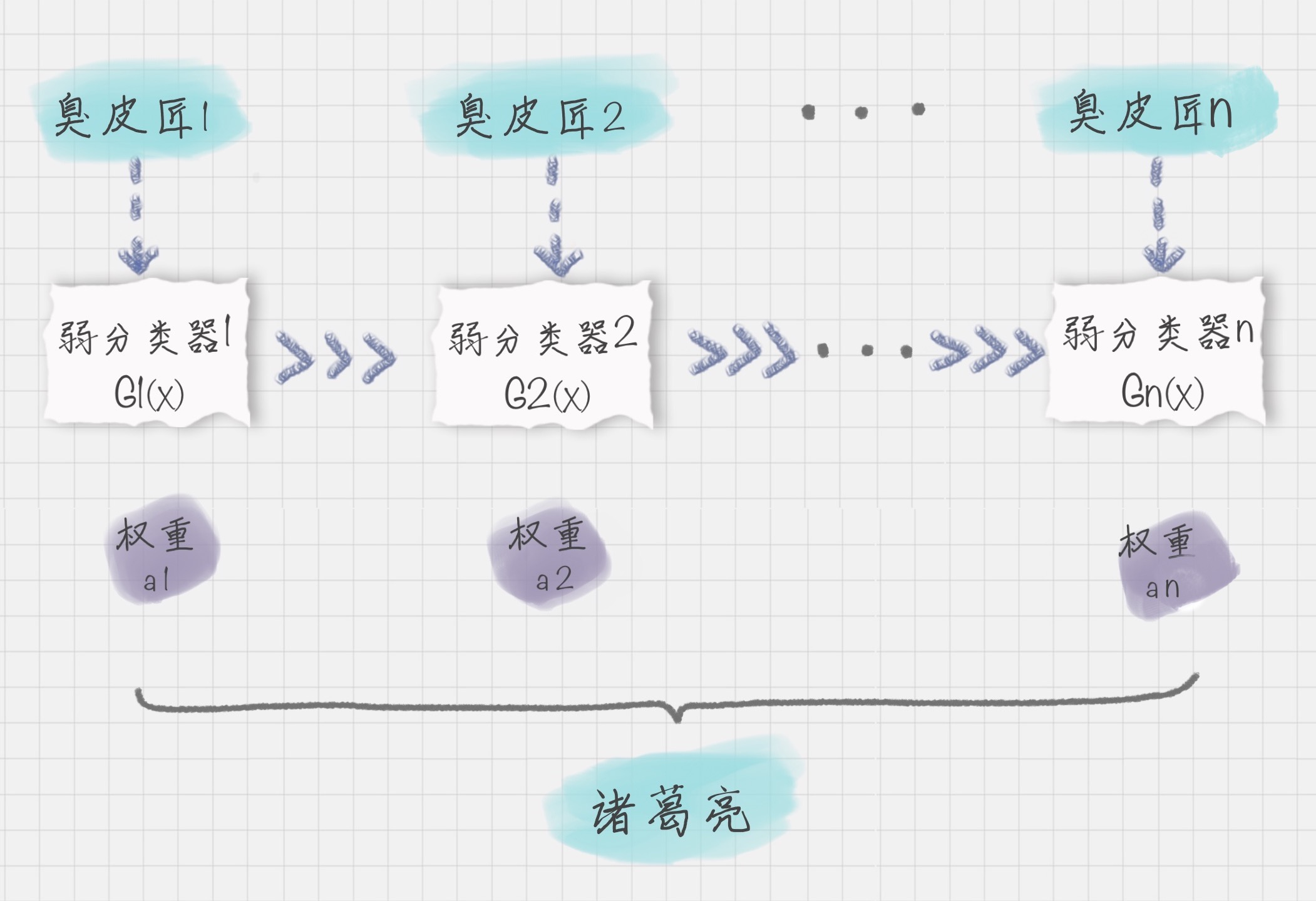

可以用上面的图来表示最终得到的强分类器，能看出它是通过一系列的弱分类器根据不同的权重组合而成的。

假设弱分类器为 Gi​(x)，它在强分类器中的权重 αi​，那么就可以得出强分类器 f(x)：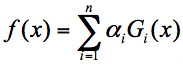

有了这个公式，为了求解强分类器，需要关注两个问题：

1.每个弱分类器在强分类器中的权重是如何计算的？

实际上在一个由 K 个弱分类器中组成的强分类器中，如果弱分类器的分类效果好，那么权重应该比较大，如果弱分类器的分类效果一般，权重应该降低。所以我们需要基于这个弱分类器对样本的分类错误率来决定它的权重，用公式表示就是：

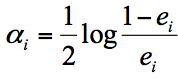
其中 ei​ 代表第 i 个分类器的分类错误率。

2.如何得到弱分类器，也就是在每次迭代训练的过程中，如何得到最优弱分类器？

实际上，AdaBoost 算法是通过改变样本的数据分布来实现的。AdaBoost 会判断每次训练的样本是否正确分类，对于正确分类的样本，降低它的权重，对于被错误分类的样本，增加它的权重。再基于上一次得到的分类准确率，来确定这次训练样本中每个样本的权重。然后将修改过权重的新数据集传递给下一层的分类器进行训练。这样做的好处就是，通过每一轮训练样本的动态权重，可以让训练的焦点集中到难分类的样本上，最终得到的弱分类器的组合更容易得到更高的分类准确率。

我们可以用 Dk+1​ 代表第 k+1 轮训练中，样本的权重集合，其中 Wk+1,1​ 代表第 k+1 轮中第一个样本的权重，以此类推 Wk+1,N​ 代表第 k+1 轮中第 N 个样本的权重，因此用公式表示为：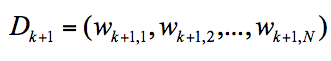

第 k+1 轮中的样本权重，是根据该样本在第 k 轮的权重以及第 k 个分类器的准确率而定，具体的公式为：

 

 

AdaBoost 算法示例

假设有 10 个训练样本，如下所示：

现在希望通过 AdaBoost 构建一个强分类器。按照上面的 AdaBoost 工作原理，来模拟一下。

首先在第一轮训练中，我们得到 10 个样本的权重为 1/10，即初始的 10 个样本权重一致，D1=(0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1)。

假设有 3 个基础分类器：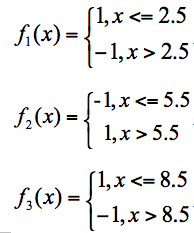

可以知道分类器 f1 的错误率为 0.3，也就是 x 取值 6、7、8 时分类错误；分类器 f2 的错误率为 0.4，即 x 取值 0、1、2、9 时分类错误；分类器 f3 的错误率为 0.3，即 x 取值为 3、4、5 时分类错误。

这 3 个分类器中，f1、f3 分类器的错误率最低，因此我们选择 f1 或 f3 作为最优分类器，假设我们选 f1 分类器作为最优分类器，即第一轮训练得到：

根据分类器权重公式得到：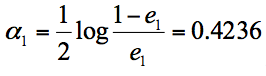

然后我们对下一轮的样本更新求权重值，代入 Wk+1,i​ 和 Dk+1​ 的公式，可以得到新的权重矩阵：D2=(0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.1666, 0.1666, 0.1666, 0.0715)。

在第二轮训练中，我们继续统计三个分类器的准确率，可以得到分类器 f1 的错误率为 0.1666*3，也就是 x 取值为 6、7、8 时分类错误。分类器 f2 的错误率为 0.0715*4，即 x 取值为 0、1、2、9 时分类错误。分类器 f3 的错误率为 0.0715*3，即 x 取值 3、4、5 时分类错误。

在这 3 个分类器中，f3 分类器的错误率最低，因此我们选择 f3 作为第二轮训练的最优分类器，即：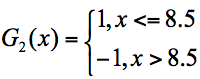

根据分类器权重公式得到：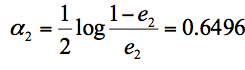

同样，我们对下一轮的样本更新求权重值，代入 Wk+1,i​ 和 Dk+1​ 的公式，可以得到 D3=(0.0455,0.0455,0.0455,0.1667, 0.1667,0.01667,0.1060, 0.1060, 0.1060, 0.0455)。

在第三轮训练中，我们继续统计三个分类器的准确率，可以得到分类器 f1 的错误率为 0.1060*3，也就是 x 取值 6、7、8 时分类错误。分类器 f2 的错误率为 0.0455*4，即 x 取值为 0、1、2、9 时分类错误。分类器 f3 的错误率为 0.1667*3，即 x 取值 3、4、5 时分类错误。

在这 3 个分类器中，f2 分类器的错误率最低，因此我们选择 f2 作为第三轮训练的最优分类器，即：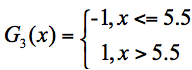

我们根据分类器权重公式得到：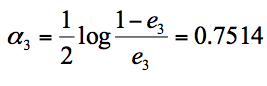

假设我们只进行 3 轮的训练，选择 3 个弱分类器，组合成一个强分类器，那么最终的强分类器 G(x) = 0.4236G1(x) + 0.6496G2(x)+0.7514G3(x)。

实际上 AdaBoost 算法是一个框架，可以指定任意的分类器，通常我们可以采用 CART 分类器作为弱分类器。通过上面这个示例的运算，体会一下 AdaBoost 的计算流程即可。

  

使用 AdaBoost 对 load_boston 进行预测

from sklearn.datasets import load_boston
from sklearn.ensemble import AdaBoostRegressor
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split

# 加载数据
data = load_boston()

# 分割数据
X_train, X_test, y_train, y_test = train_test_split(data.data, data.target, test_size=0.25, random_state=33)

# 使用AdaBoost回归模型
regressor = AdaBoostRegressor()
regressor.fit(X_train, y_train)

score = regressor.score(X_test, y_test)
print(score)

y_pred = regressor.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
print("房价预测结果: ", y_pred)
print("均方误差: ", mse)

Console Output

0.774242657651649
房价预测结果:  [20.00952381  9.58055556 14.24333333 17.04567901 24.68440367 22.19705882
 27.93066038 17.82083333 28.43238095 20.00952381 29.56304348 31.95074627
 10.61190476 24.32944785 14.51333333 25.41880342 17.62027027 15.82051282
 27.58857143 25.41880342 17.20465116 17.70847458 17.7        20.57209302
 31.43370166 18.37692308 22.1484252  24.44015748 11.08095238 29.84382022
 17.04567901 26.87647059  9.58055556 21.34807692 26.87647059 31.90300429
 26.14397163 11.6877551  14.63333333 25.41880342 15.61948052 11.27037037
 29.06287425 17.27142857 26.87647059 18.78543689 18.78543689 20.12708333
 26.87647059 20.39459459 17.04567901 32.5974359  16.590625   16.90192308
 25.41880342 21.34807692 24.68440367 17.27142857 24.68440367 22.19705882
 18.85151515 17.03636364 45.08095238 22.1484252  17.20465116 27.56438356
 26.14397163 11.27037037 17.1625     28.14854369 23.44525547 18.36190476
 17.27142857 27.56438356 19.80131579 46.27297297 16.43695652  9.51666667
 17.04567901 24.68440367 20.72372881 14.91764706 11.27037037 25.41880342
 21.0265896  21.34807692 47.24888889 16.42395833 45.01538462 32.41530055
 28.28761905 19.80131579 17.94705882 17.04567901 11.6877551  32.5974359
 24.44015748 22.96628571 17.94705882 17.94705882 15.9        20.57866667
 27.56438356 25.41880342 11.08095238 16.590625   11.32777778 26.87647059
 11.32777778 26.87647059 46.11111111 12.69615385 16.75       25.41880342
 30.45833333 24.32944785 21.34807692 21.34807692 27.5764     20.57209302
 20.57866667 17.36666667 11.32777778 21.34807692 21.63510638 17.03636364
 45.08095238]
均方误差:  17.505516582700754

Note: 由于分割的样本数据每次都不一样，所以程序每次执行的结果也会不一样。

 

Reference

https://time.geekbang.org/column/article/83915

https://time.geekbang.org/column/article/84086

https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.AdaBoostRegressor.html

https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.AdaBoostClassifier.html