EM

原创转载请注明出处：https://www.cnblogs.com/agilestyle/p/12910191.html

 

EM 聚类

EM 的英文是 Expectation Maximization，所以 EM 算法也叫最大期望算法。

 

EM 算法过程

首先初始化参数，然后再观察预期，这两个步骤实际上就是期望步骤（Expectation）。
如果结果存在偏差就需要重新估计参数，这个就是最大化步骤（Maximization）。

这两个步骤加起来也就是 EM 算法的过程。

 

EM 算法的工作原理

最大似然

英文是 Maximum Likelihood，所以最大似然也就是最大可能性的意思。举个例子，有一男一女两个同学，现在要对他俩进行身高的比较，谁会更高呢？根据经验，相同年龄下男性的平均身高比女性的高一些，所以男同学高的可能性会很大。这里运用的就是最大似然的概念。

最大似然估计

它指的就是一件事情已经发生了，然后反推更有可能是什么因素造成的。还是用一男一女比较身高为例，假设有一个人比另一个人高，反推他可能是男性。最大似然估计是一种通过已知结果，估计参数的方法。

EM 算法

EM 算法是一种求解最大似然估计的方法，通过观测样本，来找出样本的模型参数。

 

EM 聚类的工作原理

EM 算法最直接的应用就是求参数估计。如果把潜在类别当做隐藏变量，样本看做观察值，就可以把聚类问题转化为参数估计问题。这也就是 EM 聚类的原理。

相比于 K-Means 算法，EM 聚类更加灵活，比如下面这两种情况，K-Means 会得到下面的聚类结果。

因为 K-Means 是通过距离来区分样本之间的差别的，且每个样本在计算的时候只能属于一个分类，称之为是硬聚类算法。而 EM 聚类在求解的过程中，实际上每个样本都有一定的概率和每个聚类相关，叫做软聚类算法。

可以把 EM 算法理解成为是一个框架，在这个框架中可以采用不同的模型来用 EM 进行求解。

常用的 EM 聚类有

• GMM 高斯混合模型
• HMM 隐马尔科夫模型。

GMM（高斯混合模型）聚类就是 EM 聚类的一种。比如上面这两个图，可以采用 GMM 来进行聚类。和 K-Means 一样，事先知道聚类的个数，但是不知道每个样本分别属于哪一类。通常，可以假设样本是符合高斯分布的（也就是正态分布）。每个高斯分布都属于这个模型的组成部分（component），要分成 K 类就相当于是 K 个组成部分。这样可以先初始化每个组成部分的高斯分布的参数，然后再看来每个样本是属于哪个组成部分。这也就是 E 步骤。再通过得到的这些隐含变量结果，反过来求每个组成部分高斯分布的参数，即 M 步骤。反复 EM 步骤，直到每个组成部分的高斯分布参数不变为止。这样也就相当于将样本按照 GMM 模型进行了 EM 聚类。

 

sklearn 中的 GMM 聚类

几个比较主要的参数

1. n_components：即高斯混合模型的个数，也就是要聚类的个数，默认值为 1。如果不指定 n_components，最终的聚类结果都会为同一个值。

2. covariance_type：代表协方差类型。一个高斯混合模型的分布是由均值向量和协方差矩阵决定的，所以协方差的类型也代表了不同的高斯混合模型的特征。协方差类型有 4 种取值：

• covariance_type=full，代表完全协方差，也就是元素都不为 0；
• covariance_type=tied，代表相同的完全协方差；
• covariance_type=diag，代表对角协方差，也就是对角不为 0，其余为 0；
• covariance_type=spherical，代表球面协方差，非对角为 0，对角完全相同，呈现球面的特性。

3. max_iter：代表最大迭代次数，EM 算法是由 E 步和 M 步迭代求得最终的模型参数，这里可以指定最大迭代次数，默认值为 100。

 

使用 EM 算法对 load_iris 数据进行聚类

准备数据

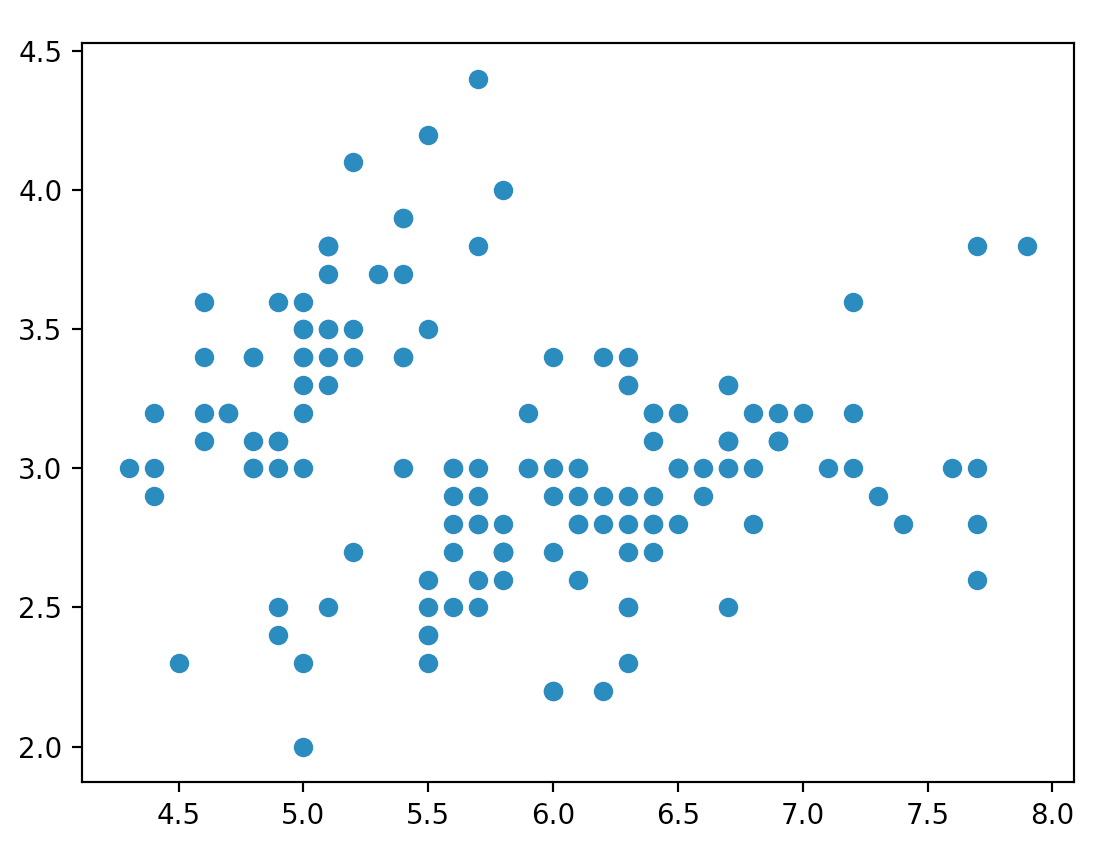
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris

iris = load_iris()

# select first two columns
X = iris.data[:, :2]

# (150, 2)
print(X.shape)

# [5.1 4.9 4.7 4.6 5.  5.4 4.6 5.  4.4 4.9 5.4 4.8 4.8 4.3 5.8 5.7 5.4 5.1
#  5.7 5.1 5.4 5.1 4.6 5.1 4.8 5.  5.  5.2 5.2 4.7 4.8 5.4 5.2 5.5 4.9 5.
#  5.5 4.9 4.4 5.1 5.  4.5 4.4 5.  5.1 4.8 5.1 4.6 5.3 5.  7.  6.4 6.9 5.5
#  6.5 5.7 6.3 4.9 6.6 5.2 5.  5.9 6.  6.1 5.6 6.7 5.6 5.8 6.2 5.6 5.9 6.1
#  6.3 6.1 6.4 6.6 6.8 6.7 6.  5.7 5.5 5.5 5.8 6.  5.4 6.  6.7 6.3 5.6 5.5
#  5.5 6.1 5.8 5.  5.6 5.7 5.7 6.2 5.1 5.7 6.3 5.8 7.1 6.3 6.5 7.6 4.9 7.3
#  6.7 7.2 6.5 6.4 6.8 5.7 5.8 6.4 6.5 7.7 7.7 6.  6.9 5.6 7.7 6.3 6.7 7.2
#  6.2 6.1 6.4 7.2 7.4 7.9 6.4 6.3 6.1 7.7 6.3 6.4 6.  6.9 6.7 6.9 5.8 6.8
#  6.7 6.7 6.3 6.5 6.2 5.9]
print(X[:, 0])

# [3.5 3.  3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 3.7 3.4 3.  3.  4.  4.4 3.9 3.5
#  3.8 3.8 3.4 3.7 3.6 3.3 3.4 3.  3.4 3.5 3.4 3.2 3.1 3.4 4.1 4.2 3.1 3.2
#  3.5 3.6 3.  3.4 3.5 2.3 3.2 3.5 3.8 3.  3.8 3.2 3.7 3.3 3.2 3.2 3.1 2.3
#  2.8 2.8 3.3 2.4 2.9 2.7 2.  3.  2.2 2.9 2.9 3.1 3.  2.7 2.2 2.5 3.2 2.8
#  2.5 2.8 2.9 3.  2.8 3.  2.9 2.6 2.4 2.4 2.7 2.7 3.  3.4 3.1 2.3 3.  2.5
#  2.6 3.  2.6 2.3 2.7 3.  2.9 2.9 2.5 2.8 3.3 2.7 3.  2.9 3.  3.  2.5 2.9
#  2.5 3.6 3.2 2.7 3.  2.5 2.8 3.2 3.  3.8 2.6 2.2 3.2 2.8 2.8 2.7 3.3 3.2
#  2.8 3.  2.8 3.  2.8 3.8 2.8 2.8 2.6 3.  3.4 3.1 3.  3.1 3.1 3.1 2.7 3.2
#  3.3 3.  2.5 3.  3.4 3. ]
print(X[:, 1])

# plot the data
plt.scatter(X[:, 0], X[:, 1])
plt.show()

样本数据分布图如下：

聚类分析

from sklearn.mixture import GaussianMixture

gmm = GaussianMixture(n_components=3)
gmm.fit(X)

labels = gmm.predict(X)
print(labels)

X0 = X[labels == 0]
X1 = X[labels == 1]
X2 = X[labels == 2]

plt.scatter(X0[:, 0], X0[:, 1], c='r')
plt.scatter(X1[:, 0], X1[:, 1], c='y')
plt.scatter(X2[:, 0], X2[:, 1], c='g')
plt.show()

结果数据分布图如下：

 

 

Summary

聚类和分类不一样，聚类是无监督的学习方式，也就是没有实际的结果可以进行比对，所以聚类的结果评估不像分类准确率一样直观，但是聚类结果的评估方式可以采用 Calinski-Harabasz 指标，代码如下：

from sklearn.metrics import calinski_harabasz_score

print(calinski_harabasz_score(X, labels))

Note：每次运行结果的指标分数可能会不一样

指标分数越高，代表聚类效果越好，也就是相同类中的差异性小，不同类之间的差异性大。当然具体聚类的结果含义，需要人工来分析，也就是当这些数据被分成不同的类别之后，具体每个类表代表的含义。

 

Reference

https://time.geekbang.org/column/article/81896

https://time.geekbang.org/column/article/82333

https://scikit-learn.org/stable/modules/generated/sklearn.mixture.GaussianMixture.html

https://scikit-learn.org/stable/modules/generated/sklearn.metrics.calinski_harabasz_score.html