使用 PCA 降维

原创转载请注明出处：https://www.cnblogs.com/agilestyle/p/12855528.html

 

特征缩放 

归一化

将一列数据变化到某个固定区间（范围）中，通常这个区间是[0, 1]

 

标准化

将数据变换为均值为0，标准差为1的分布

 

Rescaling (min-max normalization)

 

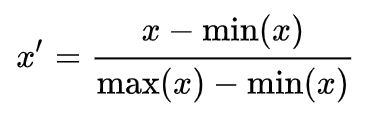
Mean normalization

 

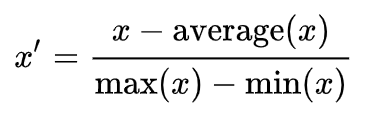
Standardization (Z-score Normalization)

 

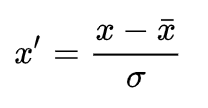
Scaling to unit length

 

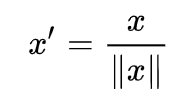
使用 MinMaxScaler 归一化

参考 min-max normalization 数学公式 进行 MinMaxScaler

import numpy as np
from sklearn.preprocessing import MinMaxScaler

X = np.array([[1, 2000], [2, 3000], [3, 4000], [4, 5000], [5, 1000]], dtype='float')
# (5, 2)
print(X.shape)
# [[1.e+00 2.e+03]
#  [2.e+00 3.e+03]
#  [3.e+00 4.e+03]
#  [4.e+00 5.e+03]
#  [5.e+00 1.e+03]]
print(X)

# max(x)
X_max = np.max(X, axis=0)
# X_max:  [   5. 5000.]
print("X_max: ", X_max)
# X_min:  [   1. 1000.]
X_min = np.min(X, axis=0)
print("X_min: ", X_min)
# max(x) - min(x)
scope = X_max - X_min
# scope:  [   4. 4000.]
print("scope: ", scope)

# mean normalization
mean = np.mean(X, axis=0)
# [   3. 3000.]
print(mean)

mn_X = (X - mean) / (X_max - X_min)
# mean normalization:
#  [[-0.5  -0.25]
#  [-0.25  0.  ]
#  [ 0.    0.25]
#  [ 0.25  0.5 ]
#  [ 0.5  -0.5 ]]
print("mean normalization: \n", mn_X)

# min-max normalization
manual_mms_X = (X - X_min) / (X_max - X_min)
# mms_X:
#  [[0.   0.25]
#  [0.25 0.5 ]
#  [0.5  0.75]
#  [0.75 1.  ]
#  [1.   0.  ]]
print("mms_X: \n", manual_mms_X)

mms = MinMaxScaler()
mms_X = mms.fit_transform(X)
# mms_X:
#  [[0.   0.25]
#  [0.25 0.5 ]
#  [0.5  0.75]
#  [0.75 1.  ]
#  [1.   0.  ]]
print("mms_X: \n", mms_X)

Note:

• MinMaxScaler：归一到 [0，1]
• MaxAbsScaler：归一到 [-1，1]

 

使用 PCA 将 mms_X 从二维降到一维

import numpy as np
from sklearn.preprocessing import MinMaxScaler

X = np.array([[1, 2000], [2, 3000], [3, 4000], [4, 5000], [5, 1000]], dtype='float')
# (5, 2)
print(X.shape)
# [[1.e+00 2.e+03]
#  [2.e+00 3.e+03]
#  [3.e+00 4.e+03]
#  [4.e+00 5.e+03]
#  [5.e+00 1.e+03]]
print(X)

# max(x)
X_max = np.max(X, axis=0)
# X_max:  [   5. 5000.]
print("X_max: ", X_max)
# X_min:  [   1. 1000.]
X_min = np.min(X, axis=0)
print("X_min: ", X_min)
# max(x) - min(x)
scope = X_max - X_min
# scope:  [   4. 4000.]
print("scope: ", scope)

# mean normalization
mean = np.mean(X, axis=0)
# [   3. 3000.]
print(mean)

mn_X = (X - mean) / (X_max - X_min)
# mean normalization:
#  [[-0.5  -0.25]
#  [-0.25  0.  ]
#  [ 0.    0.25]
#  [ 0.25  0.5 ]
#  [ 0.5  -0.5 ]]
print("mean normalization: \n", mn_X)

# min-max normalization
manual_mms_X = (X - X_min) / (X_max - X_min)
# mms_X:
#  [[0.   0.25]
#  [0.25 0.5 ]
#  [0.5  0.75]
#  [0.75 1.  ]
#  [1.   0.  ]]
print("mms_X: \n", manual_mms_X)

mms = MinMaxScaler()
mms_X = mms.fit_transform(X)
# mms_X:
#  [[0.   0.25]
#  [0.25 0.5 ]
#  [0.5  0.75]
#  [0.75 1.  ]
#  [1.   0.  ]]
print("mms_X: \n", mms_X)

from sklearn.decomposition import PCA

pca = PCA(n_components=1)
# PCA(copy=True, iterated_power='auto', n_components=1, random_state=None,
#     svd_solver='auto', tol=0.0, whiten=False)
print(pca)

# pca.fit(mms_X)
pca.fit(manual_mms_X)
# pca_X = pca.transform(mms_X)
pca_X = pca.transform(manual_mms_X)

# 2 dimensions to 1 dimension:
#  [[ 0.5 ]
#  [ 0.25]
#  [ 0.  ]
#  [-0.25]
#  [-0.5 ]]
print("2 dimensions to 1 dimension: \n", pca_X)
# 代表降维后的各主成分的方差值，方差值越大，则说明越是重要的主成分
# explained_variance_: [0.15625]
print("explained_variance_:", pca.explained_variance_)
# 代表降维后的各主成分的方差值占总方差值的比例，这个比例越大，则越是重要的主成分
# explained_variance_ratio_: [0.5]
print("explained_variance_ratio_:", pca.explained_variance_ratio_)
# 最终确定的主成分
# components_:  [[-1. -0.]]
print("components_: ", pca.components_)

inverse_pca_X = pca.inverse_transform(pca_X)
# inverse_transform:
#  [[0.   0.5 ]
#  [0.25 0.5 ]
#  [0.5  0.5 ]
#  [0.75 0.5 ]
#  [1.   0.5 ]]
print("inverse_transform: \n", inverse_pca_X)

 

使用 PCA 从三维降到二维

准备数据

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.datasets import make_blobs

# X为样本特征，Y为样本簇类别， 共10000个样本，每个样本3个特征，共4个簇
X, y = make_blobs(n_samples=10000, n_features=3, centers=[[3, 3, 3], [0, 0, 0], [1, 1, 1], [2, 2, 2]],
                  cluster_std=[0.2, 0.1, 0.2, 0.2], random_state=9)
# (10000, 3)
print(X.shape)
# (10000,)
print(y.shape)

fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(X[:, 0], X[:, 1], X[:, 2], marker='o', c=y)

ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')

plt.show()

三维数据分布图如下：

 

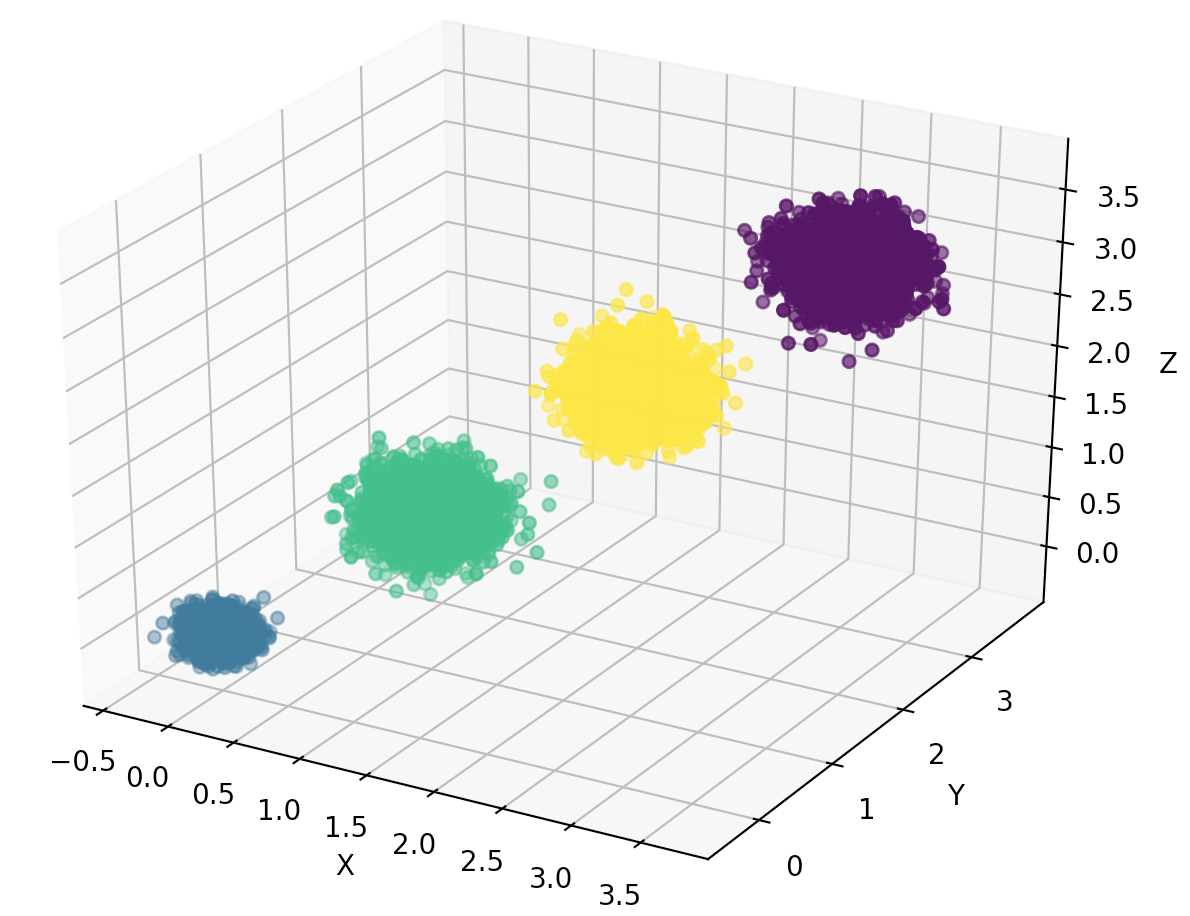
先不降维，只对数据进行投影，看看投影后的三个维度的方差分布

from sklearn.decomposition import PCA

# 先不降维，只对数据进行投影
pca = PCA(n_components=3)
pca.fit(X)
# [0.98318212 0.00850037 0.00831751]
print(pca.explained_variance_ratio_)
# [3.78521638 0.03272613 0.03202212]
print(pca.explained_variance_)

Note: 可以看出投影后三个特征维度的方差比例大约为98.3%：0.8%：0.8%。投影后第一个特征占了绝大多数的主成分比例。

 

进行降维，从三维降到二维

# 降维，从三维降到二维
pca = PCA(n_components=2)
pca.fit(X)
# [0.98318212 0.00850037]
print(pca.explained_variance_ratio_)
# [3.78521638 0.03272613]
print(pca.explained_variance_)

Note: 结果其实可以预料，因为上面三个投影后的特征维度的方差分别为：[ 3.78483785  0.03272285  0.03201892]，投影到二维后选择的肯定是前两个特征，而抛弃第三个特征。

查看此时转化后的数据分布

X_new = pca.transform(X)
plt.scatter(X_new[:, 0], X_new[:, 1], marker='o', c=y)
plt.show()

二维数据分布图如下：

 

不直接指定降维的维度，而指定降维后的主成分方差和比例，比如指定了主成分至少占95%

# 指定了主成分至少占95%
pca = PCA(n_components=0.95)
pca.fit(X)
# [0.98318212]
print(pca.explained_variance_ratio_)
# [3.78521638]
print(pca.explained_variance_)
# 1
print(pca.n_components_)

Note: 只有第一个投影特征被保留。这也很好理解，第一个主成分占投影特征的方差比例高达98%。只选择这一个特征维度便可以满足95%的阈值。

 

指定了主成分至少占99%

# 指定了主成分至少占99%
pca = PCA(n_components=0.99)
pca.fit(X)
# [0.98318212 0.00850037]
print(pca.explained_variance_ratio_)
# [3.78521638 0.03272613]
print(pca.explained_variance_)
# 2
print(pca.n_components_)

Note: 第一个主成分占了98.3%的方差比例，第二个主成分占了0.8%的方差比例，两者一起可以满足99%的阈值。

 

让MLE算法自己选择降维维度的效果

# 让MLE算法自己选择降维维度
pca = PCA(n_components='mle')
pca.fit(X)
# [0.98318212]
print(pca.explained_variance_ratio_)
# [3.78521638]
print(pca.explained_variance_)
# 1
print(pca.n_components_)

Note: 数据的第一个投影特征的方差占比高达98.3%，MLE算法只保留了第一个特征

 

Reference

https://en.wikipedia.org/wiki/Feature_scaling

https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.MinMaxScaler.html

https://scikit-learn.org/stable/modules/preprocessing.html

https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html

https://www.zhihu.com/question/20467170

https://www.cnblogs.com/pinard/p/6243025.html