Principal Component Analysis
原创转载请注明出处:https://www.cnblogs.com/agilestyle/p/12844059.html
PCA
主成分分析利用正交变换将可能存在相关性的原始属性转换成一组线性无关的新属性,并通过选择重要的新属性实现降维。
为什么降维
在机器学习中 数据被表示为向量 当数据的维度很小时,可以直接对数据进行分析和挖掘,但是在实际操作, 数据的维数可能是上万维,甚至几十万维,这时候机器学习的资源消耗是不可接受的。再者,数据的特征中往往有重叠的部分,或者线性相关的部分;因此,需要找到一种合理的方法,在减少需要分析的指标的同时,尽量减少原指标包含信息的损失,以达到对所收集数据进行全面分析的目的。
根据凡事抓主要矛盾的原则,对举足轻重的属性要给予足够的重视,无关紧要的属性则可以忽略不计,这在机器学习中就体现为降维的操作。
数据降维
- 降维就是一种对高维度特征数据的预处理方法。
- 降维是将高维度的数据保留下最重要的一些特征,去除噪声和不重要的特征,从而实现提升数据处理速度的目的。
- 在实际的生产和应用中,降维在一定的信息损失范围内,可以节省大量的时间和成本。
- 降维也成为应用非常广泛的数据预处理方法。
- 降维也有助于实现数据可视化。
主成分分析是一种主要的降维方法,它利用正交变换将一组可能存在相关性的变量转换成一组线性无关的变量,这些线性无关的变量就是主成分。多属性的大样本无疑能够提供更加丰富的信息,但也不可避免地增加了数据处理的工作量。更重要的是,多数情况下不同属性之间会存在相互依赖的关系,如果能够充分挖掘属性之间的相关性,属性空间的维度就可以降低。
在现实生活中少不了统计个人信息的场合,而在个人信息的表格里通常会包括“学历”和“学位”两个表项。因为学位和学历代表着两个独立的过程,因此单独列出是没有问题的。但在我国现行的惯例下,这两者通常会一并取得。两者之间的相关性足以让我们根据一个属性的取值去推测另一个属性的取值,因此只要保留其中一个就够了。
但这样的推测也不是永远准确。如果毕业论文的答辩没有通过,就会出现只有学历而没有学位的情形;对于在职研究生来说,只有学位没有学历的情形也不稀奇。这说明如果将学历和学位完全等同,就会在这些特例上出现错误,也就意味着信息的损失。这是降维操作不可避免的代价。
以上的例子只是简单的定性描述,说明了降维的出发点和可行性。在实际的数据操作中,主成分分析解决的就是确定以何种标准确定属性的保留还是丢弃,以及度量降维之后的信息损失。
举个例子:二维降到一维
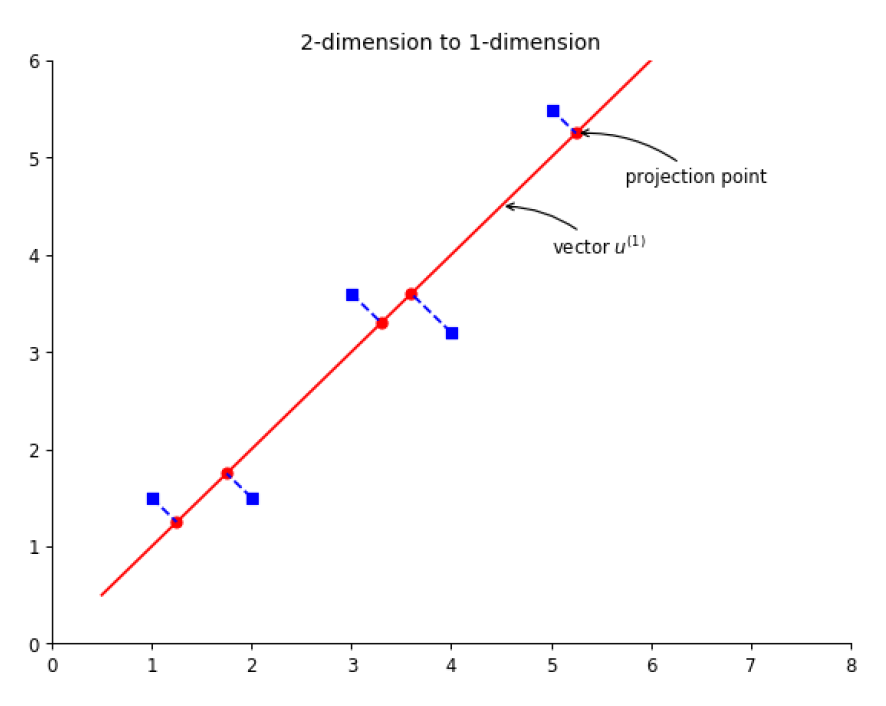
Note: 在二维空间下可以这样理解,有一个单位向量 u ,若从原点出发,这样定义 u 以后就相当于定义了一条直线。每个数据点在该直线上都有一个投影点,寻找主方向的的任务就是寻找一个 u 使得投影点的方差最大化。
PCA步骤
- 数据规范化:对 m 个样本的相同属性值求出算术平均数,再用原始数据减去平均数,得到规范化后的数据;
- 协方差矩阵计算:对规范化后的新样本计算不同属性之间的协方差矩阵,如果每个样本有 n 个属性,得到的协方差矩阵就是 n 维方阵;
- 特征值分解:求解协方差矩阵的特征值和特征向量,并将特征向量归一化为单位向量;
- 降维处理:将特征值按照降序排序,保留其中最大的 k 个,再将其对应的 k 个特征向量分别作为列向量组成特征向量矩阵;
- 数据投影:将减去均值后的 m×n 维数据矩阵和由 k 个特征向量组成的 n×k 维特征向量矩阵相乘,得到的 m×k 维矩阵就是原始数据的投影。
Note:

方差定义
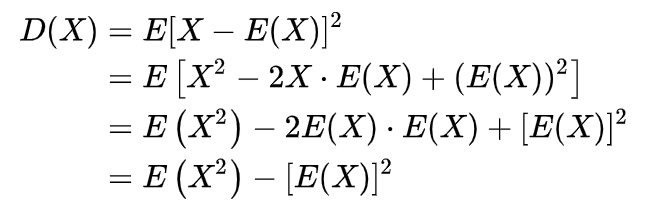
协方差定义
Cov(X,Y)=E[(X-EX)(Y-EY)] =E(XY-XEY-YEX+EXEY) =E(XY)-EXEY-EYEX+EXEY =E(XY)-EXEY
经过这几步简单的数学运算后,原始的 n 维特征就被映射到新的 k 维特征之上。这些相互正交的新特征就是主成分。需要注意的是,主成分分析中降维的实现并不是简单地在原始特征中选择一些保留,而是利用原始特征之间的相关性重新构造出新的特征;降维不是删除维度;主成分分析是将高维的数据通过线性变换投影到低维空间。
PCA的解
主成分分析的解满足最大方差和最小均方误差两类约束条件,优化目标为:1. 降维后各维度的方差尽可能大;2. 保证不同维度之间的相关性为0。
在主成分分析中,保留的主成分的数目是由用户来确定的。一个经验方法是保留所有大于 1 的特征值,以其对应的特征向量来做坐标变换。此外,也可以根据不同特征值在整体中的贡献,以一定比例进行保留。具体方法是计算新数据和原始数据之间的误差,令误差和原始数据能量的比值小于某个预先设定的阈值。
Summary
- PCA 主要用于数据降维
- 降维的主要动机有数据压缩和数据可视化
- PCA 的优点是能降低数据的复杂性
- PCA 的缺点是可能损失有用信息
主成分分析能够对数据进行降维处理,保留正交主成分中最重要的部分,在压缩数据的同时最大程度地保持了原有信息。主成分分析的优点在于完全不受参数的限制,即不需要先验的参数或模型对计算过程的人为干预,分析的结果只与数据有关。但有得必有失,这个特点的另一面是即使用户具有对训练数据集的先验知识,也没有办法通过参数化等方法加以利用。
除此之外,由于主成分分析中利用的是协方差矩阵,因而只能去除线性相关关系,对更加复杂的非线性相关性就无能为力了。解决以上问题的办法是将支持向量机中介绍过的核技巧引入主成分分析,将先验知识以非线性变换的形式体现,因而扩展了主成分分析的应用范围。
Reference
https://time.geekbang.org/column/article/2197
https://zhuanlan.zhihu.com/p/64859161
https://zh.wikipedia.org/wiki/%E5%8D%8F%E6%96%B9%E5%B7%AE
https://www.cnblogs.com/pinard/p/6239403.html



