Naive Bayes
原创转载请注明出处:https://www.cnblogs.com/agilestyle/p/12817568.html
Naive Bayes
朴素贝叶斯( Naive Bayes )是一种 基于概率 统计的分类方法。它在 条件独立 这个假设的基础上,使用 贝叶斯定理 构建算法。
概念引入
条件概率
P(A|B) = P(AB) / P(B)
乘法公式
P(B|A) = P(AB) / P(A) => P(AB) = P(A)P(B|A)
贝叶斯定理
P(A|B) = P(AB) / P(B) = P(A)P(B|A) / P(B)
Note:
- P(A) 是 A 的先验概率或边沿概率,之所以称为先验,是因为它不考虑任何 B 方面的因素
- P(A|B) 是已知 B 发生后 A 的条件概率,也由于得知 B 的取值而被称为 A 的后验概率
同理
- P(B) 是 B 的先验概率或边沿概率,之所以称为先验,是因为它不考虑任何 A 方面的因素
- P(B|A) 是已知 A 发生后 B 的条件概率,也由于得知 A 的取值而被称为 B 的后验概率
举个例子:
假设有一种病,发病率是 0.0004,患病者检验有病的概率是 99%,没病的概率是 1%;健康人检验有病的概率是 0.1%,没病的概率是 99.9%;
问:检验有病,真的有病的概率?
解:B1:患病 B2:健康 A:检验有病
P(B1) = 0.0004 P(B2) = 0.9996 P(A|B1) = 0.99 P(A|B2) = 0.001 P(A) = P(B1)P(A|B1) + P(B2)P(A|B2) = 0.0004 * 0.99 + 0.9996 * 0.001 = 0.0013956 P(B1|A) = P(B1A) / P(A) = P(B1)P(A|B1) / P(A) = 0.0004 * 0.99 / 0.0013956 = 0.284
可以总结出贝叶斯公式为:
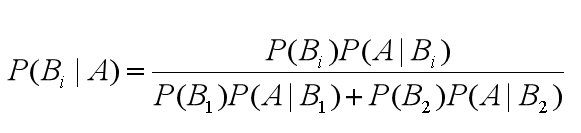
可以得出通用的贝叶斯公式:
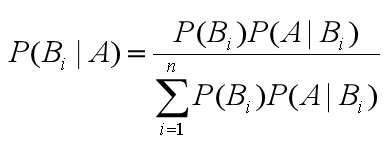
朴素贝叶斯
朴素贝叶斯,它是一种简单但极为强大的预测建模算法。之所以称为朴素贝叶斯,是因为它假设每个输入变量是独立的。这是一个强硬的假设,实际情况并不一定,但是这项技术对于绝大部分的复杂问题仍然非常有效。
朴素贝叶斯模型由两种类型的概率组成:
- 每个类别的概率P(Cj)
- 每个属性的条件概率P(Ai|Cj)
举个例子说明下什么是类别概率和条件概率。
类别概率
假设我有 7 个棋子,其中 3 个是白色的,4 个是黑色的。那么棋子是白色的概率就是 3/7,黑色的概率就是 4/7,这个就是类别概率。
条件概率
假设我把这 7 个棋子放到了两个盒子里,其中盒子 A 里面有 2 个白棋,2 个黑棋;盒子 B 里面有 1 个白棋,2 个黑棋。那么在盒子 A 中抓到白棋的概率就是 1/2,抓到黑棋的概率也是 1/2,这个就是条件概率,也就是在某个条件(比如在盒子 A 中)下的概率。
在朴素贝叶斯中,我们要统计的是属性的条件概率,也就是假设取出来的是白色的棋子,那么它属于盒子 A 的概率是 2/3。
运用贝叶斯公式: P(Bi|A) = P(Bi)P(A|Bi) / (P(B1)*P(A|B1) + P(B2)*P(A|B2)) 假设A代表白棋,B1代表A盒,B2代表B盒。 P(B1)代表A盒的概率,7个棋子,A盒有4个,所以P(B1)=4/7 P(B2)代表B盒的概率,7个棋子,B盒有3个,所以P(B2)=3/7 P(A|B1) = 1/2 P(A|B2) = 1/3 带入贝叶斯公式,可以得到: P(B1|A) = P(B1)P(A|B1) / (P(B1)*P(A|B1) + P(B2)*P(A|B2)) = (4/7 * 1/2) / ( 4/7 * 1/2 + 3/7 * 1/3)
= 2/3 最终求得取出来的是白色的棋子,那么它属于 A盒的概率 P(B1|A)= 2/3
为了训练朴素贝叶斯模型,我们需要先给出训练数据,以及这些数据对应的分类。那么类别概率和条件概率都可以从给出的训练数据中计算出来。一旦计算出来,概率模型就可以使用贝叶斯原理对新数据进行预测。
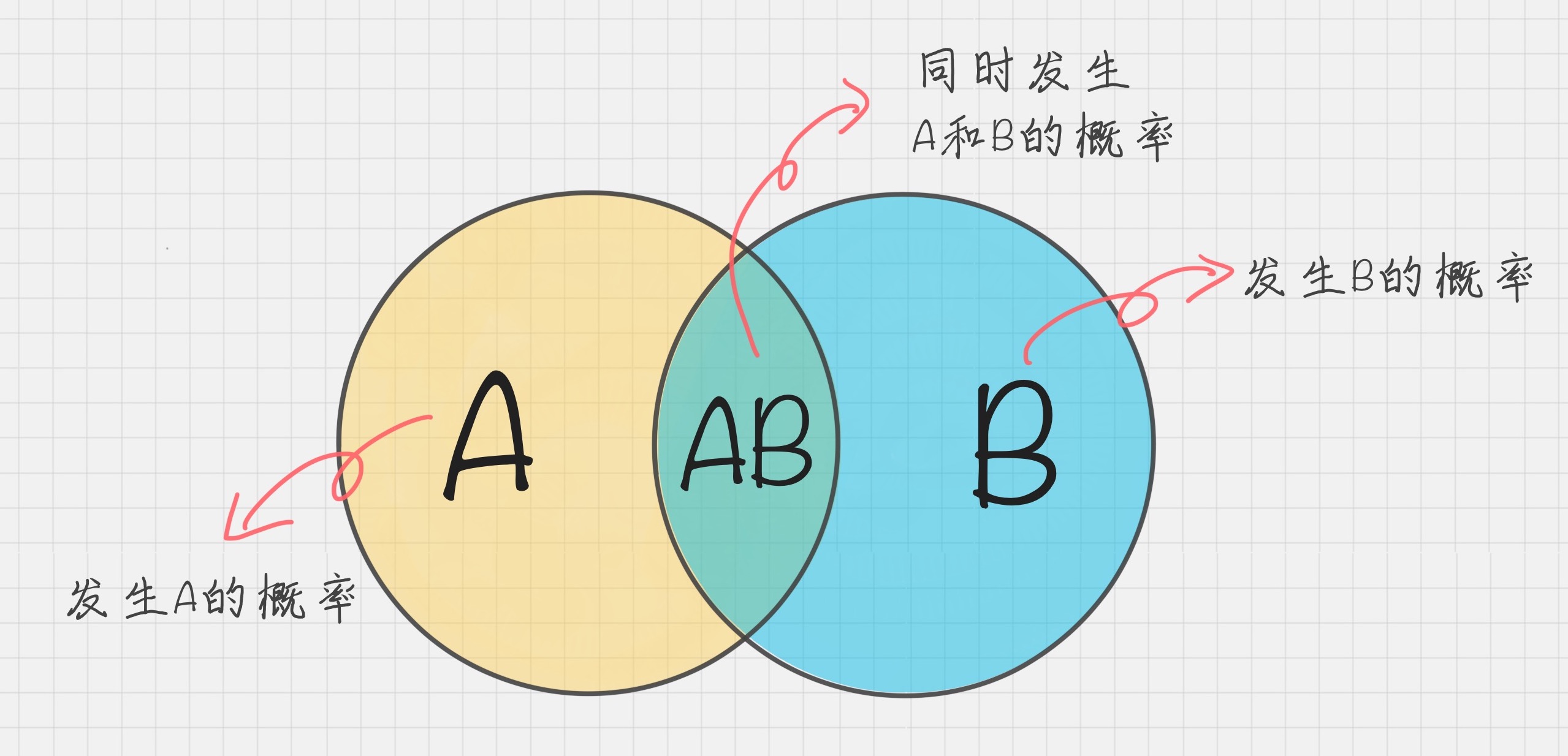
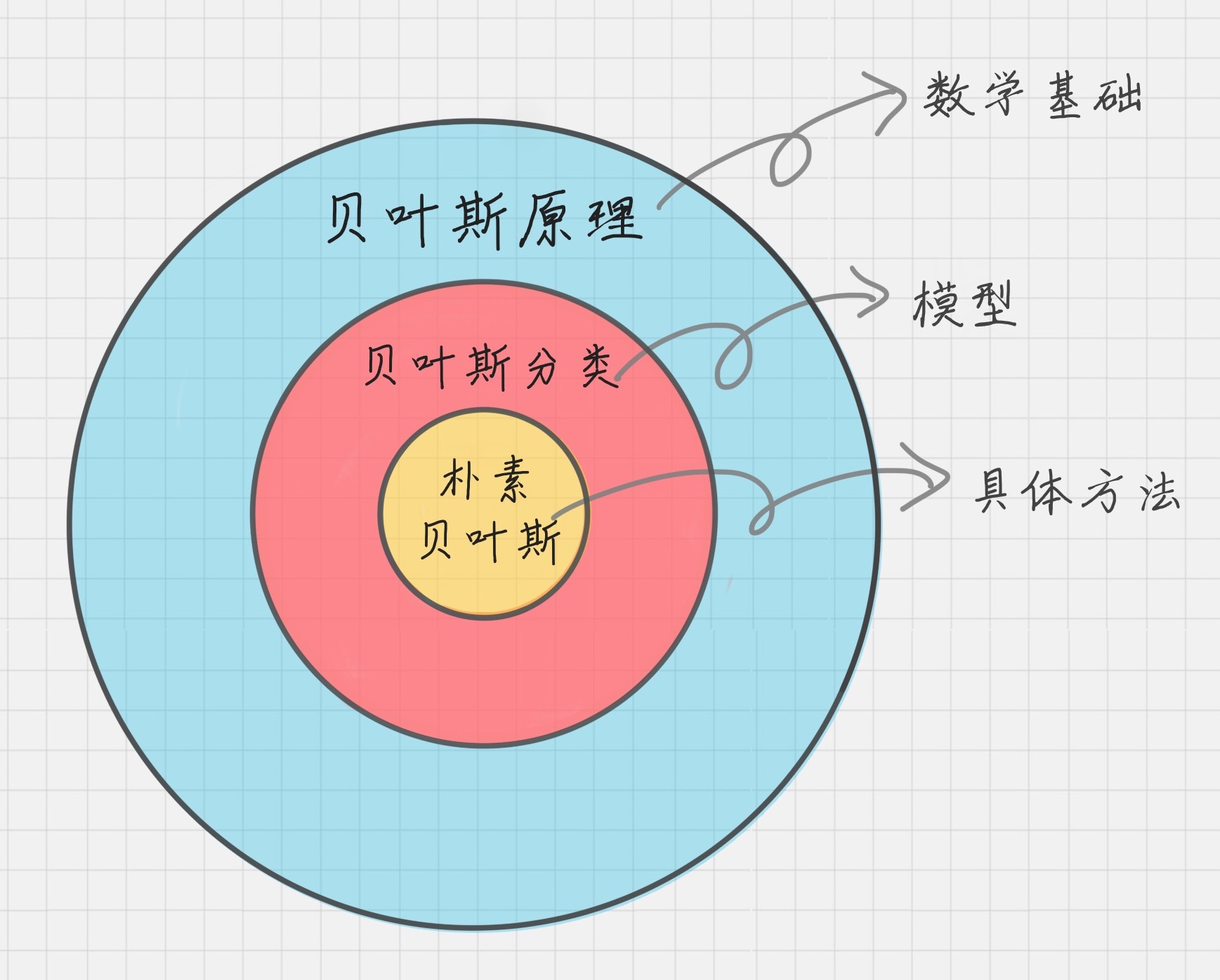
贝叶斯原理、贝叶斯分类和朴素贝叶斯这三者之间是有区别的
贝叶斯原理是最大的概念,它解决了概率论中“逆向概率”的问题,在这个理论基础上,人们设计出了贝叶斯分类器,朴素贝叶斯分类是贝叶斯分类器中的一种,也是最简单,最常用的分类器。朴素贝叶斯之所以朴素是因为它假设属性是相互独立的,因此对实际情况有所约束,如果属性之间存在关联,分类准确率会降低。不过好在对于大部分情况下,朴素贝叶斯的分类效果都不错。
朴素贝叶斯分类器工作流程
朴素贝叶斯分类常用于文本分类,尤其是对于英文等语言来说,分类效果很好。它常用于垃圾文本过滤、情感预测、推荐系统等。
流程可以用下图表示:
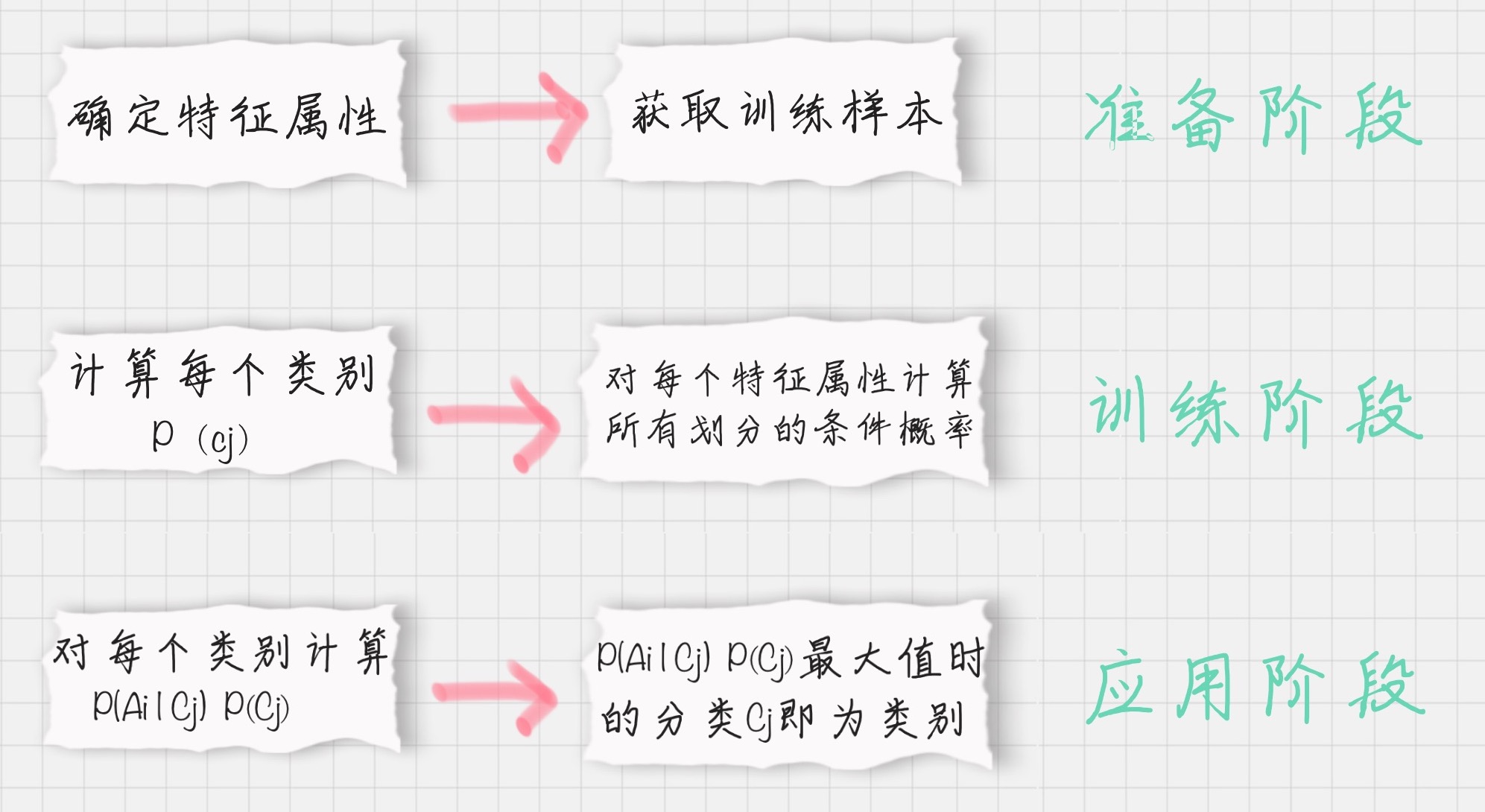
第一阶段:准备阶段
在这个阶段我们需要确定特征属性,比如“身高”、“体重”、“鞋码”等,并对每个特征属性进行适当划分,然后由人工对一部分数据进行分类,形成训练样本。这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段,其质量对整个过程将有重要影响,分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定。
第二阶段:训练阶段
这个阶段就是生成分类器,主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率。
输入是特征属性和训练样本,输出是分类器。
第三阶段:应用阶段
这个阶段是使用分类器对新数据进行分类。输入是分类器和新数据,输出是新数据的分类结果。
三种概率分布
伯努利分布(0-1 分布)
- 适用于特征向量是二进制( 0 或 1
- 两种取值出现的概率之和为 1
- 抛硬币
多项式分布
- 用于离散计数
- 满足类别分布的实验,连续做 n 次后,每种类别出现的特定次数组合的概率分布情况
- 类别分布:所有可能性之和为 1 的概率分布
- 掷骰子
高斯分布
- 适用于多个类型变量,假设特征符合高斯分布
三种不同模型应对不同概率分布
sklearn 提供了 3 个朴素贝叶斯分类算法,分别是高斯朴素贝叶斯(GaussianNB)、多项式朴素贝叶斯(MultinomialNB)和伯努利朴素贝叶斯(BernoulliNB)。
这三种算法适合应用在不同的场景下,应该根据特征变量的不同选择不同的算法:
- 伯努利朴素贝叶斯:特征变量是布尔变量,符合 0/1 分布,在文档分类中特征是单词是否出现。
- 多项式朴素贝叶斯:特征变量是离散变量,符合多项分布,在文档分类中特征变量体现在一个单词出现的次数,或者是单词的 TF-IDF 值等。
- 高斯朴素贝叶斯:特征变量是连续变量,符合高斯分布,比如说人的身高,物体的长度。
伯努利朴素贝叶斯是以文件为粒度,如果该单词在某文件中出现了即为 1,否则为 0。
多项式朴素贝叶斯是以单词为粒度,会计算在某个文件中的具体次数。
高斯朴素贝叶斯适合处理特征变量是连续变量,且符合正态分布(高斯分布)的情况。
比如身高、体重这种自然界的现象就比较适合用高斯朴素贝叶斯来处理。而文本分类是使用多项式朴素贝叶斯或者伯努利朴素贝叶斯。
代码示例
from sklearn.datasets import make_blobs from sklearn.model_selection import train_test_split from sklearn.naive_bayes import BernoulliNB, MultinomialNB, GaussianNB from sklearn.preprocessing import MinMaxScaler X, y = make_blobs(n_samples=500, centers=10, random_state=8) # (500, 2) print(X.shape) # (500,) print(y.shape) X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2) # BernoulliNB b_clf = BernoulliNB() b_clf.fit(X_train, y_train) b_score = b_clf.score(X_test, y_test) # 0.39 print(b_score) scaler = MinMaxScaler() scaler.fit(X_train) X_train_scaled = scaler.transform(X_train) X_test_scaled = scaler.transform(X_test) # MultinomialNB m_clf = MultinomialNB() m_clf.fit(X_train_scaled, y_train) m_score = m_clf.score(X_test_scaled, y_test) # 0.13 print(m_score) # GaussianNB g_clf = GaussianNB() g_clf.fit(X_train, y_train) g_score = g_clf.score(X_test, y_test) # 0.9 print(g_score)
Note: 每次运行分割的数据集是不一样的,所以打印出来的评分是不一样的
多项式朴素贝叶斯 输入的样本特征值必须是非负的,否则会抛出 ValueError: Input X must be non-negative,可以使用 MinMaxScaler 把特征值转换到(0, 1)之间
朴素贝叶斯的优缺点
优点
- 算法简单,有稳定的分类效率。
- 对小规模的数据表现很好,能个处理多分类任务,适合增量式训练,尤其是数据量超出内存时,可以一批批的去增量训练。
- 对缺失数据不太敏感。
缺点
- “朴素”的假设如果与实际情况不符,会影响模型效果。
- 输入特征数据的表现形式,比如是连续特征,离散特征还是二元特征,会影响概率计算和模型的分类效果。
Reference
https://time.geekbang.org/column/article/79294
https://time.geekbang.org/column/article/79762
https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.MinMaxScaler.html
https://scikit-learn.org/stable/modules/generated/sklearn.naive_bayes.BernoulliNB.html
https://scikit-learn.org/stable/modules/generated/sklearn.naive_bayes.MultinomialNB.html
https://scikit-learn.org/stable/modules/generated/sklearn.naive_bayes.GaussianNB.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号