KNN

原创转载请注明出处：https://www.cnblogs.com/agilestyle/p/12625721.html

 

K-Nearest Neighbor 

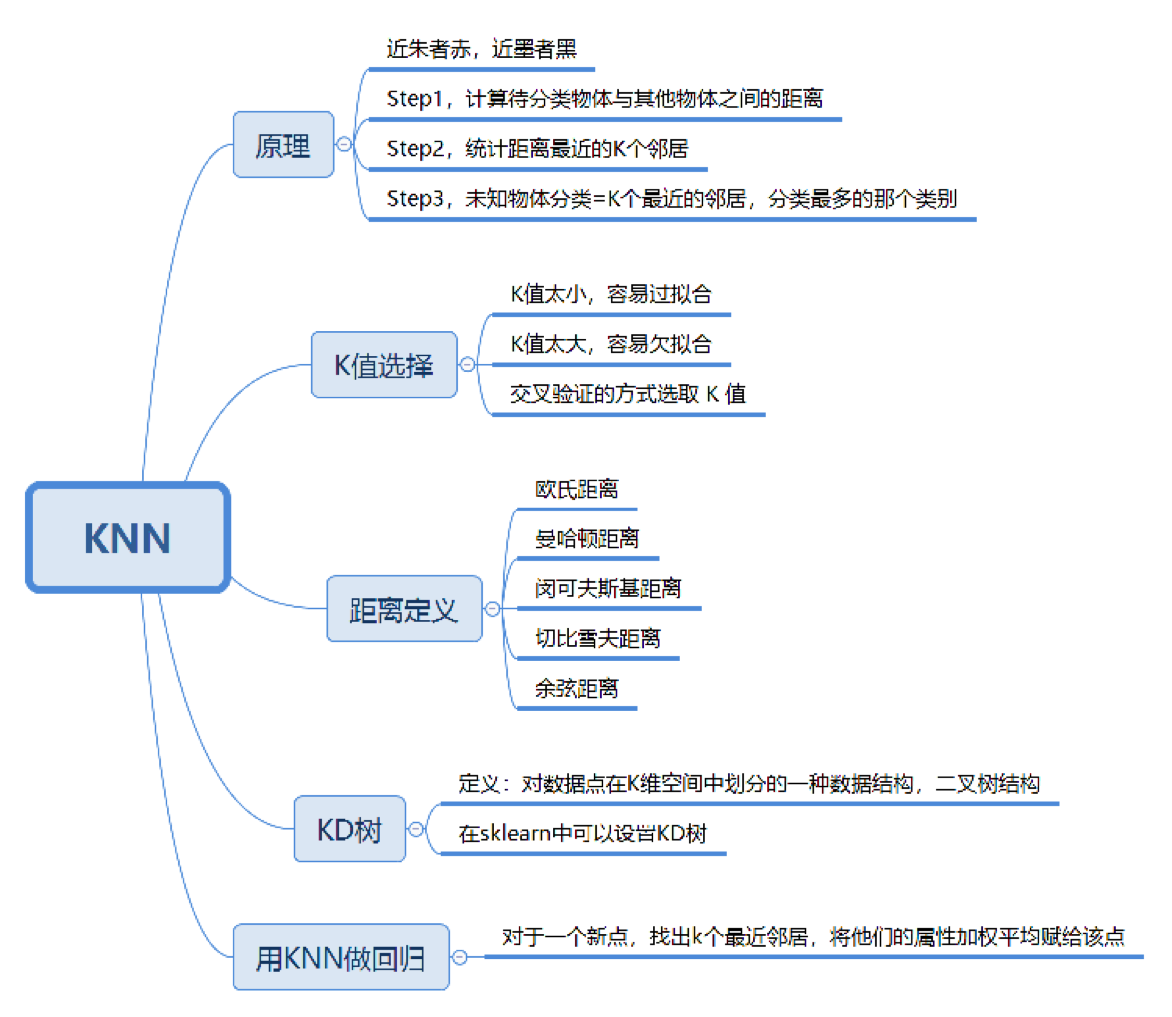
KNN是一种基本分类与回归方法

 

KNN 的工作原理

“近朱者赤，近墨者黑”可以说是 KNN 的工作原理。

整个计算过程分为三步：

1. 计算待分类物体与其他物体之间的距离；
2. 统计距离最近的 K 个邻居；
3. 对于 K 个最近的邻居，它们属于哪个分类最多，待分类物体就属于哪一类。

 

K 值如何选择

• k 值越大，模型的偏差越大，对噪声数据不敏感，可能造成模型欠拟合
• k 值越小，模型的方差就会越大，容易造成模型 过拟合
• 一般 k 的取值为 1-20
• 当 k=1 时，为最近邻算法
• scikit-learn 中， k 默认为 5

 

距离如何计算

在 KNN 算法中，还有一个重要的计算就是关于距离的度量。两个样本点之间的距离代表了这两个样本之间的相似度。距离越大，差异性越大；距离越小，相似度越大。
关于距离的计算方式有下面五种方式：

• 欧氏距离
• 曼哈顿距离
• 闵可夫斯基距离
• 切比雪夫距离
• 余弦距离

其中前三种距离是 KNN 中最常用的距离

欧氏距离是最常用的距离公式，也叫做欧几里得距离。在二维空间中，两点的欧式距离就是：

 

同理，也可以求得两点在 n 维空间中的距离：

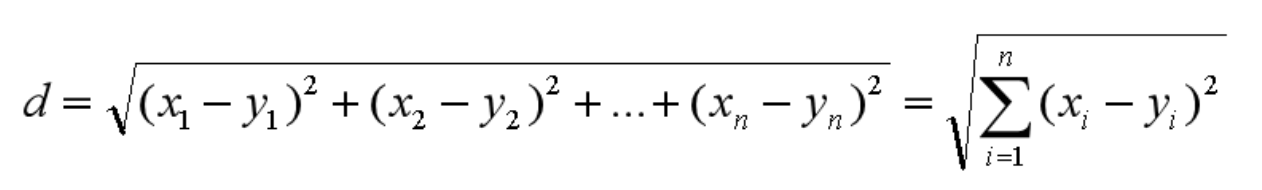
曼哈顿距离在几何空间中用的比较多。以下图为例，绿色的直线代表两点之间的欧式距离，而红色和黄色的线为两点的曼哈顿距离。

所以曼哈顿距离等于两个点在坐标系上绝对轴距总和。用公式表示就是：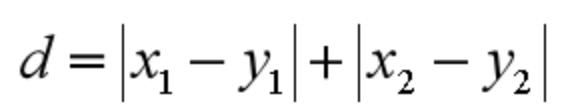

闵可夫斯基距离不是一个距离，而是一组距离的定义。对于 n 维空间中的两个点 x(x1,x2,…,xn) 和 y(y1,y2,…,yn) ， x 和 y 两点之间的闵可夫斯基距离为：

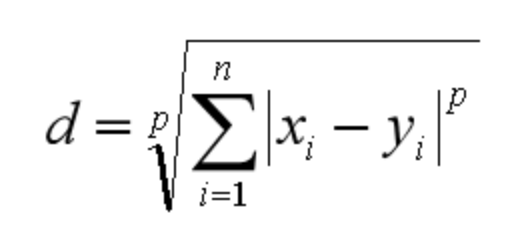
其中 p 代表空间的维数，当 p=1 时，就是曼哈顿距离；当 p=2 时，就是欧氏距离；当 p→∞ 时，就是切比雪夫距离。

 

二个点之间的切比雪夫距离就是这两个点坐标数值差的绝对值的最大值，用数学表示就是：max(|x1-y1|,|x2-y2|)。

余弦距离实际上计算的是两个向量的夹角，是在方向上计算两者之间的差异，对绝对数值不敏感。在兴趣相关性比较上，角度关系比距离的绝对值更重要，因此余弦距离可以用于衡量用户对内容兴趣的区分度。比如我们用搜索引擎搜索某个关键词，它还会给你推荐其他的相关搜索，这些推荐的关键词就是采用余弦距离计算得出的。

 

KD 树

KNN 的计算过程是大量计算样本点之间的距离。为了减少计算距离次数，提升 KNN 的搜索效率，人们提出了 KD 树（K-Dimensional 的缩写）。KD 树是对数据点在 K 维空间中划分的一种数据结构。在 KD 树的构造中，每个节点都是 k 维数值点的二叉树。既然是二叉树，就可以采用二叉树的增删改查操作，这样就大大提升了搜索效率。
在这里，我们不需要对 KD 树的数学原理了解太多，你只需要知道它是一个二叉树的数据结构，方便存储 K 维空间的数据就可以了。而且在 sklearn 中，我们直接可以调用 KD 树，很方便。

 

KNN 回归

KNN 不仅可以做分类，还可以做回归。

• 分类 —— 如果想要对未知电影进行类型划分，首先看一下要分类的未知电影，离它最近的 K 部电影大多数属于哪个分类，这部电影就属于哪个分类，这就是一个分类问题。

• 回归 —— 如果是一部新电影，已知它是爱情片，想要知道它的打斗次数、接吻次数可能是多少，这就是一个回归问题。

 

KNN 算法优缺点

优点：

• 准确性高
• 对异常值和噪声有较高的容忍度

缺点

• 计算量较大
• 对内存的需求也较大（每次对一个未标记样本进行分类时，都需要全部计算一遍距离）

 

Summary

 

Reference

https://time.geekbang.org/column/article/80983