线性回归
Reference: https://developers.google.com/machine-learning/crash-course/descending-into-ml/linear-regression
linear regression
每分钟的虫鸣叫声与温度(摄氏度)的关系

此曲线图表明温度随着鸣叫声次数的增加而上升。鸣叫声与温度之间的关系是线性关系,可以绘制一条直线来近似地表示这种关系。
线性关系

虽然该直线并未精确无误地经过每个点,但针对我们拥有的数据,清楚地显示了鸣叫声与温度之间的关系。只需运用一点代数知识,就可以将这种关系写下来,如下所示:
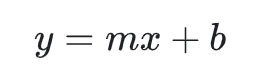
其中:
- y 指的是温度(以摄氏度表示),即我们试图预测的值。
- m 指的是直线的斜率。
- x 指的是每分钟的鸣叫声次数,即输入特征的值。
- b 指的是y轴截距。
按照机器学习的惯例,需要写一个存在细微差别的模型方程式:
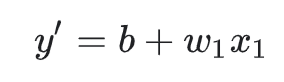
其中:
- y' 指的是预测标签(理想输出值)。
- b 指的是偏差(y 轴截距)。而在一些机器学习文档中,它称为 w0 。
- w1 指的是特征 1 的权重。权重与上文中用 表示的“斜率”的概念相同。
- x1 指的是特征(已知输入项)。
要根据新的每分钟的鸣叫声值 x1 推断(预测)温度 y',只需将 x1 值代入此模型即可。
下标(例如 w1 和 x1 )预示着可以用多个特征来表示更复杂的模型。例如,具有三个特征的模型可以采用以下方程式:
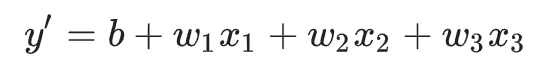
强者自救 圣者渡人


