bzoj 2115 Xor (线性基)

Input

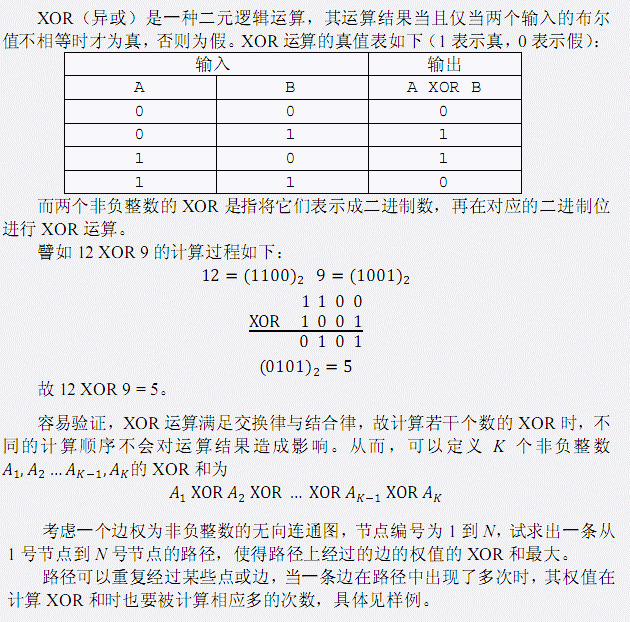
第一行包含两个整数N和 M， 表示该无向图中点的数目与边的数目。 接下来M 行描述 M 条边，每行三个整数Si，Ti ，Di，表示 Si 与Ti之间存在 一条权值为 Di的无向边。 图中可能有重边或自环。

Output

仅包含一个整数，表示最大的XOR和（十进制结果）,注意输出后加换行回车。

Sample Input

5 7
1 2 2
1 3 2
2 4 1
2 5 1
4 5 3
5 3 4
4 3 2

Sample Output

6

HINT

 

 
网上看了一个题解写的很好
引用:  http://www.cnblogs.com/ljh2000-jump/p/5869925.html

这道题要求从1到n的最大xor和路径，存在重边，允许经过重复点、重复边。那么在图上作图尝试之后就会发现，路径一定是由许多的环和一条从1到n的路径组成。容易发现，来回走是没有任何意义的，因为来回走意味着抵消。考虑这道题求得是路径xor和最大，所以必然我们要想办法处理环的情况。我的做法是任意地先找出一条从1到n的路径，把这条路径上的xor和作为ans初值（先不管为什么可行），然后我们的任务就变成了求若干个环与这个ans初值所能组合成的xor最大值。显然，我们需要预处理出图上所有的环，并处理出所有环的环上xor值，这当然是dfs寻找，到n的路径的时候顺便求一下就可以了。

　　当我们得到了若干个环的xor值之后，因为是要求xor最大值，我们就可以构出这所有xor值的线性基。构出之后，再用ans在线性基上取max就可以了。

　　现在我们来讨论上述做法的可行性。

　　第一种情况：我们对最终答案产生贡献的某个环离1到n的主路径很远，这样的话，因为至少可以保证1可以到达这个环，那么我们可以走到这个环之后绕环一周之后原路返回，这样从1走到环的路上这一段被重复经过所以无效，但是环上的xor值被我们得到了，所以我们并不关心这个环和主路径的关系，我们只关心环的权值。

　　第二种情况：我们任意选取的到n的路径是否能保证最优性。假设存在一条更优的路径从1到n，那么这条路径与我们原来的路径构成了一个环，也就会被纳入线性基中，也会被计算贡献，假如这个环会被经过，那么最后的情况相当于是走了两遍原来选取的路径，抵消之后走了一次这个最优路径，所以我们无论选取的是哪条路径作为ans初值，都可以通过与更优情况构成环，然后得到一样的结果。这一证明可以拓展到路径上的任意点的路径选取。

　　这样我们就可以完美解决了。我第一次WA了一发，因为我没有考虑到ans初值不为0，在线性基上取到xor的max的时候，不能单纯以ans这一位是否为0来决定是否异或上基的这一位，必须要看异或之后取一个max做一个判断才行。

 

 1 #include <bits/stdc++.h>
 2 
 3 using namespace std;
 4 typedef long long ll;
 5 const int maxn = 550000+500;
 6 bool vis[maxn];
 7 ll cir[maxn],ans;
 8 int cntcir = 0;
 9 ll p[63];
10 ll w[maxn],dx[maxn];
11 struct edge
12 {
13     int to,nxt;
14     ll v;
15 }e[maxn];
16 int last[maxn];
17 int cnte = 0;
18 void addedge (int u,int v,ll w)
19 {
20     e[++cnte].to=v;e[cnte].nxt=last[u];last[u]=cnte;e[cnte].v=w;
21     e[++cnte].to=u;e[cnte].nxt=last[v];last[v]=cnte;e[cnte].v=w;
22 }
23 void dfs (int x)
24 {
25     vis[x] = 1;
26     for (int i=last[x];i!=0;i=e[i].nxt){
27         if (!vis[e[i].to]){
28             dx[e[i].to] =dx[x] ^ e[i].v;
29             dfs(e[i].to);
30         }
31         else cir[++cntcir] = dx[x]^dx[e[i].to]^e[i].v;
32     }
33 }
34 int n,m;
35 int main()
36 {
37     //freopen("de.txt","r",stdin);
38     while (~scanf("%d%d",&n,&m)){
39         memset(vis,false,sizeof vis);
40         memset(last,0,sizeof last);
41         memset(dx,0,sizeof dx);
42         memset(p,0,sizeof p);
43         cntcir = 0;
44         cnte = 0;
45         for (int i=0;i<m;++i){
46             int x,y;ll z;
47             scanf("%d%d%lld",&x,&y,&z);
48             addedge(x,y,z);
49         }
50         dfs(1);
51         ll ans = dx[n];
52         for (int i=1;i<=cntcir;++i){
53             for (int j=62;j>=0;--j){
54                 if ((cir[i])>>j&1){
55                     if (p[j]){
56                         cir[i]^=p[j];
57                     }
58                     else{
59                         p[j]=cir[i];
60                         break;
61                     }
62                 }
63             }
64         }
65         for (int i=62;i>=0;--i){
66             if ((ans^p[i])>ans)
67                 ans^=p[i];
68         }
69         printf("%lld\n",ans);
70     }
71     return 0;
72 }

 

 

posted @ 2017-10-10 21:33  抓不住Jerry的Tom  阅读(206)  评论(0)  编辑  收藏  举报