平衡二叉树之AVL树的学习比较
2011-04-19 12:01 Aga.J 阅读(1148) 评论(0) 编辑 收藏 举报平衡二叉树(这里就不解释了):给予不同的平衡条件,造就出不同的效率表现,以及不同的实现复杂度,AVL ,RB, AA都是一种平衡二叉树,因为维护平衡,所以插入和删除节点的平均时间长了,但是可以避免不平衡的情况,所以元素的搜寻访问时间短了!而最直观的平衡条件是整棵树的深度为logN,也就是说要求每个节点的左右子树有相同的高度(递归定义的结果就是该树的叶子节点都在同一层上!)
接下来是AVL树 : AVL树,原名是Adelson-Velskii-Landis tree,它没有像上述那个条件要求那么苛刻,它允许任何节点的左右子树的高度相差1,(递归定义的结构就是该树的叶子节点只可以在最后一层和倒数第二层)
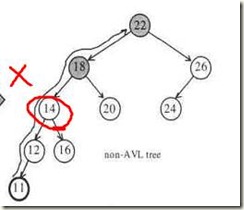
下面分析“插入节点”情况下几种使得AVL树不平衡的情况以及解决方法
一旦插入节点后,AVL树不平衡,只要调整“插入点到根节点”的那条路径上,平衡状态被破坏的所有节点中 最深的那个,就可以使得整棵树重新获得到平衡,假设该节点为X,
那么有以下四种情况
1 插入点位于X 的左子节点的左子树 ----左左 (外侧)//不管是在左子树的什么位置上插入
2 插入点位于X的左子节点的右子树 -- 左右 (内侧)
3 插入点位于X的右子节点的左子树 (外侧)
4 插入点位于X的右子节点的右子树 (内侧)
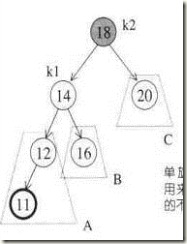
在外侧插入—也就是在 完成外侧插入后,某个顶点成为第一个违反平衡条件,是下面这种状态(违反点为k2)也就是情况【1】【4】
1 插入点位于X 的左子节点的左子树 ----左左 (外侧)
4 插入点位于X的右子节点的右子树 (内侧)
插入11后,使得A子树成长了一层,但是这样并不会让k1树不平衡,但是A子树的深度却比C子树的深度多2,也就使得k2的左子树的高度为3,k2的右子树的高度为1,破坏了平衡。而且这种情况下,B子树不可能和A子树同层,不然的话早就不平横了,同时B子树也不可能和C子树同层,不然的话第一个违反平衡条件的就是k1而不是k2了。
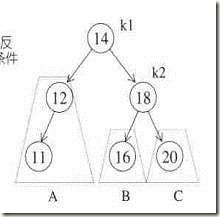
我们希望A子树向上提,而C子树下降一层,可以从图里这样想象,只需要把K1向上提,而K2自然下滑,并且把B子树挂到K2的左侧,就完成了这个过程(因为本身AVL是一颗平衡二叉树,子树有一定的大小关系,所以这样操作可以得到正确的结果)右右插入的时候同理!
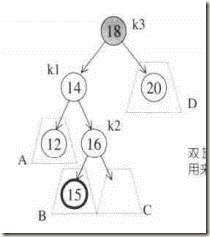
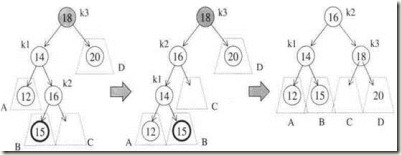
在内侧插入 – 也就是在情况【2】,【3】
2 插入点位于X的左子节点的右子树 -- 左右 (内侧)
3 插入点位于X的右子节点的左子树 (外侧)
这次我们没办法对k1和k3只进行一次旋转,使得k1为根节点来完成平衡。我们可以考虑用k2节点来作为平衡树的根,这就需要两次旋转
对照着上述的旋转方法,给出基本的旋转操作(暂时不考虑其他节点为空的情况)
Void singleRotation( Node* n,bool left) //n节点表示当前节点违反了平衡条件
{
Node *newHead;
If(left==TRUE) //新插入的节点在n的左子树
//左左,进行右上提拉节点,注意只适合左子节点的左子树,如果是左子节点的右子树,则需//要两次旋转
{
newHead = n->left;
if(newHead->right!=null)
n->left=newHead->right;
newHead->right=n;
n=newHead;
}
Else //右右,进行左上提拉节点
{
newHead = n->right;
if(newHead->left!=null)
n->right= newHead->left;
newHead->left = n;
n= newHead;
}
}
Void doubleRotation(Node* n, bool left)
{
If(left == TRUE) //新插入的节点在n的左子树
//左右,注意只适合左子节点的右子树,如果是左子节点的右子树,值需要一次旋转
{
singleRotation(n->left,false);
singleRotation(n,true);
}
Else
{
singleRotation(n->right,true);
singleRotation(n,true);
}
}
作者:Aga.J
出处:http://www.cnblogs.com/aga-j
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。
个人学习笔记仅供本人记录知识所用,不属发表性文章。