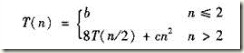分治算法的学习笔记

分治算法

一个简单的可以利用分治思想来解决的问题是在一个一维数组中找到最大值和最小值，最暴力的做法就是分两次完成，第一次从数组中找到最大值，第二次从数组中找到最小值。这种方法并不高效，比较次数多，而原因是 在选择最大值，最小值的时候是“孤立”的进行的，并不利用上次比较的信息【重点，利用上次比较的信息！】。

使用分治法可以避免这个缺点。算法实现如下：

Void getMaxAndMin(int list[],int &max, int &min, int low, int high) //low,high是分治的必须

{

If(low == high ) { max= list[low]; min=list[low];}

Else if (high = low+1)

{

If (list[low]<list[high])

{ max=list[high];min=list[low];return;}

Else

{ max= list[low]; min=list[high] ; return ;}

}

Else

{

Int mid= ( low+high )/2;

Int max1,min1;

getMaxAndMin(list,max1,min1,low,mid);

int max2,min2;

getMaxAndMin(list,max2,min2,mid+1,high);

if( max1>max2) max=max1;else max=max2;

if(min1>min2) min=min1;else min=min2;

}

}

上面的2分分治算法的时间复杂度可以计算得到：

在一般情况下，假设将规模为n的问题分解问哦n/b 的a个子问题，消耗的时间代价为d(n),那么分治法的时间复杂度的方程为

T(n) = 1 当n=1时

T(n) = aT(n/b) + d(n) 当n!=1时

将递归展开，最终得到T(n)的关于n的函数。

第一项称为齐次解，当d(n)等于0时函数的最终解救是第一项，也就是说第一项，齐次解救代表了所有子问题求解的代价。

而第二项则表示将所有子问题结合起来的代价，也称为特解。

对这个时间复杂度函数进行分析我们可以知道，如果“其次解”部分比较大，那么找到姜子问题结合起来的更快的方法，将不会影响该分治法的时间复杂度级别，这种情况下，我们应该找到一种方法，将一个问分解为更多的子问题，从而影响齐次解，看看能不能得到更低的时间复杂性级别。而如果驱动函数超过了齐次解，就要尽量减低驱动函数开销（当驱动函数为乘法函数时，可以求解到源函数的特解）

分治法应用：

Strassen矩阵乘法：

问题：假设矩阵A，B为n*n的矩阵，求A*B。

一般的解决方法：C中的元素ij，需要将A的第i行的n个元素和B的第j列的n个元素对应相乘得到的乘积再相加得到。这样一来，求得C内的一个元素需要n次乘法和n-1次加法。这里乘法开销较大，忽略加法的开销，所以时间开销是O(n的3次方)。

应用分治法：将A，B看成是由4个大小相等的n/2 * n/2的子矩阵构成的。进行下面的运算

计算时间开销：现在变成了8个n/2*n/2的小矩阵的乘法，任意两个小矩阵相乘都，都会得到一个n/2*n/2的矩阵，再得到8个小矩阵后，还要进行4*n^2/4次加法才能得到C中每个元素的值，假设加法的代价是c则可以得到下面的开销

根据上面的推导结果，这个递归方程的解为O(n^3)。所以时间复杂度内并没有改善，所以我们只能在上述公式中想办法减少乘法（上述式子要8次乘法）

这样一来，乘法的次数就减少到7次，递归方程的解

顺序统计：

问题：例如要挑出某一线性序列中的第i个最大整数。

解决方案：最暴力的方法就是先对整个序列进行排序，再提取第i个整数

不过我们可以利用一些排序算法（例如快速排序）的特性，免去多余的排序过程，找到第i个元素。

假设使用类似快速排序的方法，找出第n/2个最大结点。根据快速排序算法过程，我们选择第一个结点为pivot，经过第一次分段后，比该pivot大的在其右边，比它小的在其左边。那么如果右边刚好有n/4个节点（左边则有3*n/4 -1个节点，而我们的目标节点是第n/2个最大的节点，所以我们只需要在左边部分寻找第(3*n/4 -1 – n/2)个最大节点即可），那么我们只需要在pivot的左边寻找第n/4-1个最大的节点就可以。【假设：在该pivot左边中我们再选一个pivot，如果这时pivot的右边有n/4-2个节点，那么这个pivot就是第n/2个最大节点】

用这种类似于快速排序的方法找出第k个最大节点，启发我们：如果每一次分段之后，尽可能地多排除一些结点，那么算法就有可能在O(n)的时间内找到要求的节点，而做到尽可能的排除节点，就要选择“好”的pivot。

使用“消去法”来查找“线性序列”中的第i个大的节点。

1） 假设k>=5 是一个任意选择的奇数（k表示子序列的长度）

2） 如果 n < 3k 使用一般排序法来求，直接访问第i个节点

3） 如果n >=3k 将A划分为f=n/k个含有k个节点的子序列

4） 对f个子序列B1，。。Bf各自进行排序，然后找出它们的中间节点-第（k+1）/2个b1,b2..bf。然后用消去法在对得到的b1,b2,bf找出中间数M（第(f+1)/2或者第f/2），这个M是一个比较接近真正处于中间的那个数，然后根据这个比较接近中间的数来进行分段

5） 假设j是A中大于或者等于M的节点的个数，如果j等于i，那么M就是结果。

如果j>i，那么使用j-1作为新的n值，从序列A中除去所有小于M的节点，再用消去法球A中剩下的节点所构成的序列中的第i个大的数。

(也就是说第i大的数在比M大的数集合中，所以消除所有小于M的节点，再从中找第i大的数)

如果j<i，这用n-j作为新的n值，并从序列A中除去大于等于M的所有节点。然后再用消去法求第i-j个大的节点

（也就是说 第i大的数在比M小的数的集合中，所以消除所有大于或者等于M的节点，然后再从中找第i-j个大的节点）

Template<class Type>

Void selectSort(Type a[],int j1,int j2) //简单选择排序

{

Int p,q,k;

Type aux;

For( p=j1 ;p<j2 ;p++)

{

K=p ;

For( q=p=1 ;q<=j2 ;q++)

If ( a[q]<a[k]) k=q ;

If ( k != p) { aux=a[p] ;a[p]=a[k] ;a[k]=aux ;}

}

}

Template<class Type>

Type pick(Type a[],int i, int n, int k)

{

If ( n<3*k) {select(a,1,n); return a[n-i+1];} //算法第二步

Else

{

Type *B;

Type M;

Int f,j,v,t;

B = new Type[n/k+1]; //B用来保存每个子序列的中间节点

F = n/k; //子序列个数

For(t = 1;t<=f;t++) //将子序列进行排序并保存中间节点

{

Select (a,(t-1)*k+1,t*k);

B[t]=a[(t-1)*k + (k+1)/2];

}

T=f/2+1;

M = pick(B,t,f,k); //算法三提及的，确定中间结点M

//B共有f个元素，取第t大的，k是分组依据

J=0;

For(t=1;t<n;t++)

if( a[t]>=M )

j++; //求得大于等于M的结点总数

if(j==i) return M; //如果刚好j==i，那么第i个大的结点就是M

if ( j> i)

{

V = 1;

For (t=1; t<=n;t++)

If ( a[t]>M)

a[v++]=a[t]; //将比M小的数用大于M的数覆盖，得到的长度为j-1

//（消去法的思想）

return pick(a,I,j-1,k); //如果j>i，则在大于等于M的j-1个节点中找第i大

}

Else

{

V=1;

For(t=1;t<=n;t++)

If ( a[t] < M )

A[v++]=a[t]; //将比M大数用比M小的数覆盖得到n-j的长度

//消去法的思想

Return pick(a,I-j,n-j,k);

//如果j < i，则在小于等于M的n-j个节点中招第i-j大

}

}

}