Llama2-笔记

简介

• paper ： https://arxiv.org/abs/2307.09288
• code ：https://github.com/facebookrese
• 解释 : https://zhuanlan.zhihu.com/p/649756898

处理流程

预处理文本

输入：文本(问题)

处理：文本向量(Tokenization)，文本转数字。一维向量

输出-1：Embedding，更进一步把单个数字转换成一组向量。二维向量(矩阵)

输出-2：位置编码(transformer)，区分不同位置的Token，并为模型提供上下文关系的信息。

生成

Transformer ：在生成任务中，模型只需要用到Transformer 的decoder阶段，即Decoder-Only，比如GPT、LLaMA 都是。

LLM这种生成式的任务是根据给定输入文本序列的上下文信息预测下一个单词或token，所以LLM模型通常只需要使用到Transformer Decoder部分，而所谓Decoder相对于Encoder就是在计算Q*K时引入了Mask以确保当前位置只能关注前面已经生成的内容。

自回归生成：在生成任务中，使用自回归（Autoregressive）方式，即逐个生成输出序列中的每个Token。在解码过程中，每次生成一个Token时，使用前面已生成的内容作为上下文，来帮助预测下一个Token。

模型结构

Input tensor shape: [batch size, seq length, hidden dim]

• batch size: 多少条句子
• seq length: 单条句子长度
• hidden dim：其实就是embedding的长度

Llama 2的模型结构与标准的Transformer Decoder结构基本一致，主要由32个 Transformer Block 组成，不同之处主要包括以下几点：

• 前置的RMSNorm层

• Q在与K相乘之前，先使用RoPE进行位置编码

• K V Cache，并采用Group Query Attention

• FeedForward层

RMSNorm

Transformer中的Normalization层一般都是采用LayerNorm来对Tensor进行归一化

其中 γ 和 β 为可学习的参数

\[LayerNorm:y =\frac{x-E[x]}{\sqrt{Var[x]+\epsilon}}*\gamma+\beta \\ 均值: E[x] =\frac1N\sum_{i=1}^Nx_i \\ 方差: Var[x] =\frac1N\sum_{i=1}^N(x_i-E[x])^2 \]

RMSNorm省去了求均值的过程(均值为0),也没有了偏置 β

\[RMSNorm:y =\frac{x}{\sqrt{Mean(x^{2})+\epsilon}}*\gamma \\ 均值为0的方差: Mean(x^{2}) =\frac1N\sum_{i=1}^Nx_i^2 \]

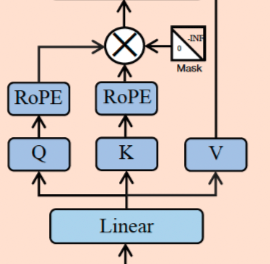
Attention

如何划分出Q、K和V

直接看代码片段

# 定义
self.wq = ColumnParallelLinear(
            args.dim,
            args.n_heads * self.head_dim,    # Q的头数* head_dim
            bias=False,
            gather_output=False,
            init_method=lambda x: x,
        )
self.wk = ColumnParallelLinear(
            args.dim,
            self.n_kv_heads * self.head_dim, # K的头数* head_dim
            bias=False,
            gather_output=False,
            init_method=lambda x: x,
)
self.wv = ColumnParallelLinear(
            args.dim,
            self.n_kv_heads * self.head_dim, # V的头数* head_dim
            bias=False,
            gather_output=False,
            init_method=lambda x: x,
)
# 划分
bsz, seqlen, _ = x.shape
xq, xk, xv = self.wq(x), self.wk(x), self.wv(x)

xq = xq.view(bsz, seqlen, self.n_local_heads, self.head_dim)
xk = xk.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)
xv = xv.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)

xq, xk = apply_rotary_emb(xq, xk, freqs_cis=freqs_cis) #嵌入RoPE位置编码

其余部分和transformer差不多

KV cache

原始的KV计算

每次计算K和V是都需要全部计算一次。

cache

Q可以是一个词的一维向量，而K，V是上下文信息的二维矩阵。实际上在计算式K，V的更新是缓慢的(没有太大变化)，并不需要每次都重新计算。因此可以把之前的信息保留下来，来一个新的词就添加进去，来防止K，V重复计算。这样就不需要计算K和V的二维矩阵(原始的KV计算)，只需要计算一维向量即可(KV cache)。

def mha(x, c_attn, c_proj, n_head, kvcache=None):  # x: [n_seq, n_embd] -> [n_seq, n_embd]
    # qkv projection
    # when we pass kvcache, n_seq = 1. so we will compute new_q, new_k and new_v
    x = linear(x, **c_attn)  # [n_seq, n_embd] -> [n_seq, 3*n_embd]
    # split into qkv
    qkv = np.split(x, 3, axis=-1)  # [n_seq, 3*n_embd] -> [3, n_seq, n_embd]
    if kvcache:
        # qkv
        new_q, new_k, new_v = qkv  # new_q, new_k, new_v = [1, n_embd]
        old_k, old_v = kvcache
        k = np.vstack([old_k, new_k]) # k = [n_seq, n_embd], where n_seq = prev_n_seq + 1
        # 此处的 +1 就是 new_k, new_v = [1, n_embd]
        v = np.vstack([old_v, new_v]) # v = [n_seq, n_embd], where n_seq = prev_n_seq + 1
        qkv = [new_q, k, v]

RoPE位置编码

原始的绝对位置编码

在标准的Transformer中通常是在整个网络进入Transformer Block之前做一个位置编码：

编码方式：

\[f_{\{q,k,v\}}(x_{i},i) =W_{\{q,k,v\}}(x_{i}+p_{i}) \\ p_{i,2t} =sin(\frac i{10000^{\frac{2t}{d}}}) \\ p_{i,2t+1} =cos(\frac{i}{10000^{\frac{2t}{d}}}) \]

旋转位置编码

一般来说，绝对位置编码具有实现简单、计算速度快等优点，而相对位置编码则直接地体现了相对位置信号(当前词的位置与其他词的相对位置信息)，跟我们的直观理解吻合，实际性能往往也更好。

ROPE：通过绝对位置编码的方式实现相对位置编码

==============================================