现代管理理论与技术-整数规划-参考

4-1.高压容器公司制造小、中、大三种尺寸的金属容器，所用资源为金属板、劳动力
和机器设备，制造一个容器所需的各种资源的数量如表4-1所示。不考虑固定费用，每种容
器售出一只所得的利润分别为4万元、5万元、6万元，可使用的金属板有500吨，劳动力
有300人月，机器有100台1月，此外不管每种容器制造的数量是多少，都要支付一笔固定
的费用:小号是100万元，中号为150万元，大号为200万元。试制定一个生产计划，使获
得的利润为最大?请建立相关数学模型。

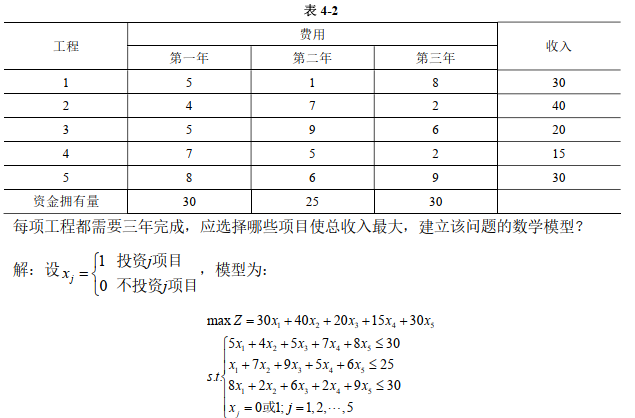
4-2.某公司今后三年内有五项工程可以考虑投资，每项工程的期望收入和年度费用(万
元)如表4-2所示。

4-3.某部门一周中每天需要不同数目的雇员:周一到周四每天应至少需要50人，周
五至少需要80人，周六周日每天至少需要90人，现规定应聘者需要连续工作5天，试确定
聘用方案，即周一到周日每天聘用多少人，在满足需要的条件下聘用总人数最少?请建立相.
关数学模型。

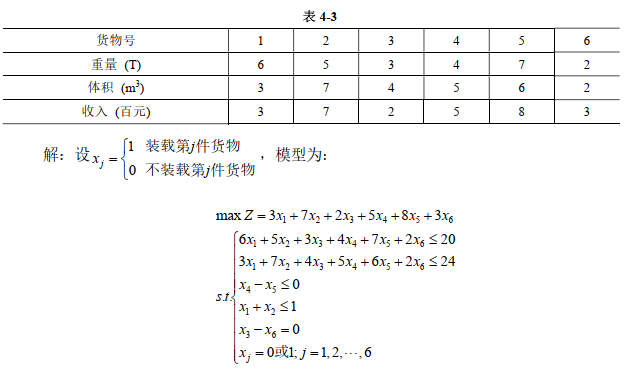
4-4.一辆货车的有效载重量是20吨，载货有效空间是8mx2mx1.5m。现有六件货物可
供选择运输，每件货物的重量、体积及收入如表43所示。另外，在货物4和5中优先运货
物5，货物1和2不能混装，货物3和货物6要么都不装要么同时装。怎样安排货物运输使
收入最大，建立数学模型?

4-5.某打井队要从10个可供选择的井位中确定5个进行探油，使总的探油费用最小。
若10个井位的代号为S, S2, S.... S1o,相应的探油费用为c, c2, ......并且井位选择
要满足下列限制条件: (1) 或选择Sq和S，或选择Sg; (2) 选择了S;或S，就不能选S;
(3)在S、So,、ST、Ss中最多只能选两个。试建立线性规划模型?

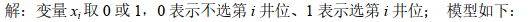
4-6.用匈牙利法求解指派问题(求:min) ?