机器学习——欧式距离和余弦距离

在数据分析和挖掘的过程中，为了知道个体间差异的大小，我们需要去评价个体之间的相似性，数据的挖掘方法可以分为分类和聚类，如KNN和KMeans.

而衡量个体差异的方法主要分为两种，距离度量——欧式距离，相似度度量——余弦距离。

 

1、欧式距离

　　衡量个体在空间上存在的距离，距离越远说明个体间的差异越大。

根据欧几里得公式： 计算出每个点之间的绝对距离，对于欧式距离公式，求其倒数将范围规定与(0,1),对于值越靠近与1的则相似度越高

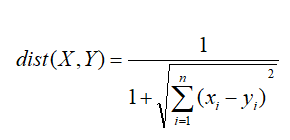
2、余弦距离

　　余弦距离也称为余弦相似度，是用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小的度量，

当两个向量的方向接近于一致，夹角趋于0则两个向量就相近，也可以称两个个体之间相似。

将三角形的两边a,b当作向量：

求其夹角公式如下：

关于相似度和余弦距离的关系如下图：角度越小则相似度越高

3、举例分析

假设5个用户对喜欢的水果进行打分如下形成一个DataFrame：

val spark = SparkSession.builder().appName("euclidean").master("local[*]").getOrCreate()
    val schema = StructType(Seq(
      StructField("userid",StringType,false),
      StructField("apple",DoubleType,false),
      StructField("banana",DoubleType,false),
      StructField("orange",DoubleType,false),
      StructField("watermelon",DoubleType,false),
      StructField("melon",DoubleType,false)
    ))
    val df = spark.createDataFrame(spark.sparkContext.parallelize(Seq(
      Row("nol",4.5,5.0,0.0,3.0,0.0),
      Row("no2",0.0,0.0,5.0,4.0,0.0),
      Row("no3",4.0,3.0,4.5,0.0,4.0),
      Row("no4",0.0,0.0,0.0,0.0,5.0),
      Row("no5",4.0,3.0,2.0,1.0,0.0)
    )),schema)

 

求欧式距离：

每一个用户需要对每一个水果都要求解欧式距离，假设当前用户:arr1，比较用户:arr2

定义函数如下：

//欧氏距离公式
  def calcEuc(arr1:Array[Double],arr2:Array[Double])={
    val lst:ListBuffer[Double] = ListBuffer[Double]()
    for (num1<-0 until arr1.length;num2<-0 until arr2.length;if num1==num2){
      lst.append(math.pow(arr1(num1)-arr2(num2),2))
    }
    1/(1+math.sqrt(lst.sum)) //求出接近于1则用户之间更相似
  }

//查相似度（每两个用户间相似度）
  def eucli(rdd:List[Array[Double]])={
    val lst:ListBuffer[ListBuffer[Double]] = ListBuffer[ListBuffer[Double]]()
    for (arr<-rdd){
      val sec:ListBuffer[Double]=ListBuffer[Double]()
      for(a1<-rdd){
        //计算欧式距离公式
        sec.append(calcEuc(arr,a1))
      }
      lst.append(sec)
    }
    lst
  }

 

求解如下：

val cls = df.columns.filter(x => x != "userid").map(x=>col(x))
    val rdd = df.select(concat_ws(",", cls: _*).alias("feature")).rdd.toLocalIterator.toList.map(r => {
      val arr = r(0).toString.split(",").map(x => x.toDouble)
      arr
    })
    val res =eucli(rdd)
    res.foreach(x=>x.foreach(println))


1.0
0.10592130260593688
0.12444584824196174
0.10098718092501505
0.2222222222222222
0.10592130260593688
1.0
0.1167355195593027
0.10960059084055324
0.13231996486433337
0.12444584824196174
0.1167355195593027
1.0
0.12819304429541925
0.17176743283130236
0.10098718092501505
0.10960059084055324
0.12819304429541925
1.0
0.11881849050177154
0.2222222222222222
0.13231996486433337
0.17176743283130236
0.11881849050177154
1.0

 

求余弦距离：

1#求点积

 //点积
  def dj(arr1:Array[Double],arr2:Array[Double])={
    val lst:ListBuffer[Double]=ListBuffer[Double]()
    for(num1<-0 until arr1.length;num2<- 0 until arr2.length;if num1==num2){
      lst.append(arr1(num1)*arr2(num2))
    }
    lst.sum
  }

 

2#求模

//向量求模
  def mod(vec:Array[Double])={
    math.sqrt(vec.map(math.pow(_,2)).sum)
  }

 

3#余弦相似度公式

def calcCos(arr1:Array[Double],arr2:Array[Double])={
    dj(arr1,arr2)/(mod(arr1)*mod(arr2))
  }

 

4#相似度计算

  //查相似度（每两个用户间相似度）
  def eucli(rdd:List[Array[Double]])={
    val lst:ListBuffer[ListBuffer[Double]] = ListBuffer[ListBuffer[Double]]()
    for (arr<-rdd){
      val sec:ListBuffer[Double]=ListBuffer[Double]()
      for(a1<-rdd){
        //计算余弦相似度
       sec.append(calcCos(arr,a1))
      }
      lst.append(sec)
    }
    lst
  }

 

求解如下：

val cls = df.columns.filter(x => x != "userid").map(x=>col(x))
    val rdd = df.select(concat_ws(",", cls: _*).alias("feature")).rdd.toLocalIterator.toList.map(r => {
      val arr = r(0).toString.split(",").map(x => x.toDouble)
      arr
    })
    val res =eucli(rdd)
    res.foreach(x=>x.foreach(println))

1.0000000000000002
0.25444237836283273
0.5724809269635496
0.0
0.892363919068504
0.25444237836283273
1.0
0.44899090442330025
0.0
0.39918616395854073
0.5724809269635496
0.44899090442330025
0.9999999999999999
0.5111012519999519
0.7931681071869339
0.0
0.0
0.5111012519999519
1.0
0.0
0.892363919068504
0.39918616395854073
0.7931681071869339
0.0
1.0