随机数求最值、均值及排序的问题分析

思路分析：

对于这种随机数求最值的问题，有两种解决的方法：

　　1、可以将生成的随机数进行排序，排序完成后数组中的第一个数和最后一个数就是要求的最值；

　　2、可以假设一个最值，并将数组中的随机数依次与其比较，如：需要一个最小值，则可以假设一个在定义域之外的数 t，比它小则将值传给 t,最后的t必定是最小值。

下面将以一个例子用两种方法来计算：

# 随机生成10个1~1000之间的不重复随机数，求平均值、最小值，最大值，并降序排序。#

法一：

　　　　

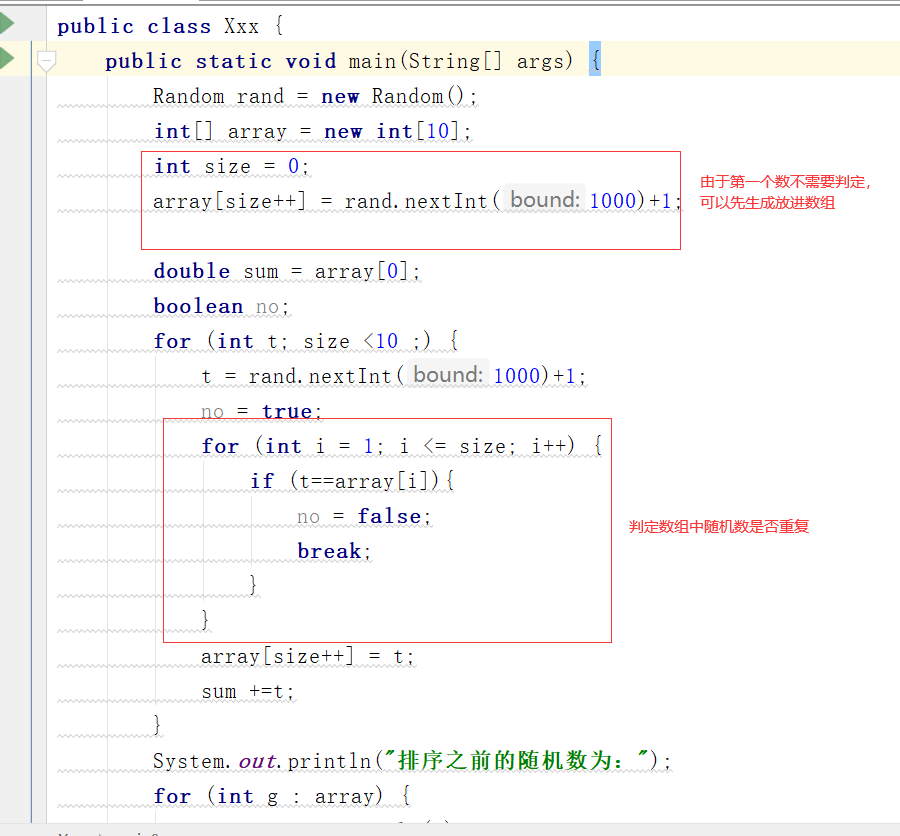
　　首先考虑生成随机数是否会出现重复的问题，由于第一个数必定不会重复，可以优先生成放进数组里面；
　　然后需要考虑的是后面生成的随机数是否有可能与前面的数发生重复的情况，若重复则一直重新生成，否则将其放入数组；
　　由于需要求平均值，在这我用sum代表和，均值可能出现有小数的情况，数据类型我用了double.
　　
　　
　　下面考虑的是排序，由于排序之后就可以得到最值，所以可以放在一起考虑，在这我用的是插入排序：
　　　　对于降序的排序，若出现下标i的数小于i-1的数，则会自动排序；
　　　　若下标为i的数值大则赋值给临时变量，并依次与左边的数进行比较，找到第一个比它大的数并插入与它的右边.

　　　　

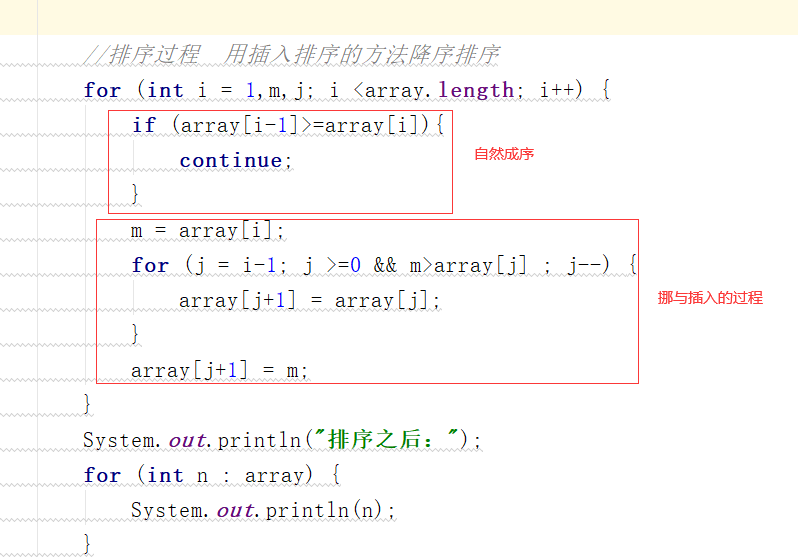
　　　　在降序排序完成之后，array[0]的位置就是最大值，而array[9]的位置就是最小值：

　　　　

　　法二：
　　　　对于随机数的生成和降序排序与上面一样，考虑不同的是对最值的求解方式，
　　首先随机生成随机数，在求最大值的时候，给max赋值一个比定义域小的数，再循环遍历找到数组中的最大值

　　
　　　同理求最小值的情况，给min赋值一个比定义域要大的数，再遍历找到数组中的最小值
　　
　　
　　针对不同的情况可以使用不同的方法，若需要对数组进行排序的话，考虑第一种方法就比较简单，
因为不需要考虑最值的求解过程，在排序完成的时候，最值也就解出了，而不需要对数组进行排序的话，
直接求解最值，则可以考虑第二种方法，可以省略掉排序的过程。